利用scipy.optimize求解投资组合的有效边界
本文例子是基于道琼斯指数、墨西哥MXX指数、日经225、富时100四个指数来构建有效前沿,思路很简单,在给定组合的收益率下,寻找最小方差的投资比例,然后分别取不同的组合收益率,寻找对应的最小方差;那么这个过程如何在python中实现呢?可以利用scipy.optimize中的minimize函数进行求解,代码如下:
# -*- coding: utf-8 -*-
"""
计算有效边界上的mean-std组合
@author: solon
"""
import pandas as pd
import numpy as np
from scipy.optimize import minimize
df1=pd.read_csv(r'Z:\User\data\data_indexes.csv') #读取指数收益率数据
mean_r=np.array(df1.mean())
df2=df1.cov()
def std(x0):
'''计算给定权重下的组合的标准差'''
ww=np.array(x0)
std=np.dot(np.dot(ww,np.array(df2)),ww.T)
return std
x0=[0.1,0.2,0.3,0.4] #任意给定一个初始投资比例
l_r=[]
l_std_1=[]
l_std_2=[]
for r in np.linspace(-0.0033,0.015,100):
cons1=({'type':'eq','fun':lambda x: np.sum(x)-1},{'type':'eq','fun':lambda x: np.dot(x,mean_r.T)-r}) #等式类型的约束条件,约束条件为投资比例之和为1,以及组合收益率为r
cons2=({'type':'eq','fun':lambda x: np.sum(x)-1},{'type':'eq','fun':lambda x: np.dot(x,mean_r.T)-r},{'type':'ineq','fun':lambda x:x[0]},{'type':'ineq','fun':lambda x:x[1]},{'type':'ineq','fun':lambda x:x[2]},{'type':'ineq','fun':lambda x:x[3]}) #包含不等式约束,增加了投资比例都非负这样的约束条件
res1=minimize(std,x0,method='SLSQP',constraints=cons1) #minimize函数中的第一个参数std表示要最小化的目标函数,x0为ndarray,表示目标函数中的待求解的未知变量,以std的第一个参数的形式传入,需要一个初始值
res2=minimize(std,x0,method='SLSQP',constraints=cons2)
l_r.append(r)
l_std_1.append(res1.fun)
l_std_2.append(res2.fun)
df=pd.DataFrame([l_r,l_std_1,l_std_2]).T
df.columns=['return','sigma_uncons','sigma_cons']
#对得到的df进行处理,以方便后续作图
df2['return_unlimited']=df['return']
df2['return_limited']=df['return']
df2.columns=['return','sigma','sigma_cons','return_unlimited','return_limited']
#可视化,可利用DataFrame中的ax参数在同一个坐标系中画图,这样就不仅仅可以实现共享x轴作图,也可以变相的实现共享y轴作图
ax=df2.plot('sigma_cons','return_limited')
df2.plot('sigma','return_unlimited',ax=ax).figure运行的可视化结果如下:
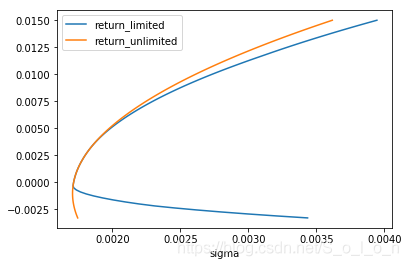
以上就是一个简单的例子展示,关键在于如何使用minimize函数,使用方法已经在代码的注释中详细说明,对于更具体的minimize函数的用法,可参考其文档https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html