深入浅出图神经网络|GNN原理解析☄学习笔记(五)图信号处理与图卷积神经网络
深入浅出图神经网络|GNN原理解析☄学习笔记(五)图信号处理与图卷积神经网络
文章目录
图信号处理(
Graph Signal Processing,
GSP)是
离散信号处理(
Discrete Signal Processing,
DSP)理论在图信号领域的应用,其通过对傅里叶变换、滤波等信号处理基本概念的迁移,来研究对图信号的压缩、变换、重构等信号处理的基础任务。
图信号处理与图卷积模型密不可分:一方面,理解图信号处理对于了解图卷积模型的定义和演变有十分重要的帮助;一方面,图信号处理也为卷积模型的理论研究提供了十分实用的工具。
矩阵乘法的三种形式
设两个矩阵 A ∈ R K × M A∈R^{K×M} A∈RK×M, B ∈ R M × P B∈R^{M×P} B∈RM×P,对于 C = A B C=AB C=AB,有如下三种计算方式:
-
内积视角:将A视作一个行向量矩阵,将B视作一个列向量矩阵,则:
C i j = A i , ; B : , j C_{ij}=A_{i,;}B_{:,j} Cij=Ai,;B:,j -
行向量视角:将B视作一个行向量矩阵,将A视作系数矩阵,则:
C i , : = ∑ m M A i m B m , : C_{i,:}=\sum_m^MA_{im}B_{m,:} Ci,:=m∑MAimBm,: -
列向量视角:将A视作一个列向量矩阵,将B视作系数矩阵,则:
C : , j = ∑ m M B m j A : , m C_{:,j}=\sum_m^MB_{mj}A_{:,m} C:,j=m∑MBmjA:,m
图信号与图的拉普拉斯矩阵
拉普拉斯矩阵(Laplacian Matrix)是用来研究图的结构性质的核心对象,拉普拉斯矩阵的定义如下:
L
=
D
−
A
L=D-A
L=D−A,D是一个对角矩阵,
D
i
i
=
∑
j
A
i
j
D_{ii}=\sum_jA_{ij}
Dii=∑jAij表示的是节点
v
i
v_i
vi的度。拉普拉斯矩阵的元素级别定义如下:
L
i
j
=
{
d
e
g
(
v
i
)
i
f
:
i
=
j
−
1
i
f
:
e
i
j
∈
E
0
o
t
h
e
r
w
i
s
e
L_{ij}=\begin{cases} deg(v_i) \quad if: i = j\\ -1 \quad if:e_{ij}∈E\\ 0 \quad otherwise \end{cases}
Lij=⎩⎪⎨⎪⎧deg(vi)if:i=j−1if:eij∈E0otherwise
拉普拉斯矩阵的正则化形式(symmetric normalized laplacian)
L
s
y
m
=
D
−
1
/
2
L
D
−
1
/
2
L_{sym}=D^{-1/2}LD^{-1/2}
Lsym=D−1/2LD−1/2,元素级别定义如下:
L
i
j
=
{
1
i
f
:
i
=
j
−
1
d
e
g
(
v
i
)
d
e
g
(
v
j
)
i
f
:
e
i
j
∈
E
0
o
t
h
e
r
w
i
s
e
L_{ij}=\begin{cases} 1 \quad if: i = j\\ \frac{-1}{\sqrt{deg(v_i)deg(v_j)}} \quad if:e_{ij}∈E\\ 0 \quad otherwise \end{cases}
Lij=⎩⎪⎪⎨⎪⎪⎧1if:i=jdeg(vi)deg(vj)−1if:eij∈E0otherwise
拉普拉斯矩阵的定义来源于拉普拉斯算子,拉普拉斯算子是n维欧式空间中的一个二阶微分算子:
Δ
f
=
∑
i
=
1
n
δ
2
f
δ
x
i
2
\Delta f=\sum_{i=1}^{n}\frac{δ^2f}{δx_i^2}
Δf=∑i=1nδxi2δ2f
。如果将该算子的作用域退化到离散的二维图像空间,就成了我们非常熟悉的边缘检测算子,其作用原理如下:
Δ
f
(
x
,
y
)
=
δ
2
f
(
x
,
y
)
δ
x
2
+
δ
2
f
(
x
,
y
)
δ
y
2
=
[
f
(
x
+
1
,
y
)
+
f
(
x
−
1
,
y
)
+
f
(
x
,
y
+
1
)
+
f
(
x
,
y
−
1
)
]
−
4
f
(
x
,
y
)
\Delta f(x,y)=\frac{δ^2f(x,y)}{δx^2}+\frac{δ^2f(x,y)}{δy^2}\\ =[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)
Δf(x,y)=δx2δ2f(x,y)+δy2δ2f(x,y)=[f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)]−4f(x,y)
在处理图像时,上式子中的算子会被表示成模板的形式:
0 1 0
1 -4 1
0 1 0
从模板中可以直观地看到,拉普拉斯算子描述了中心像素与局部上、下、左、右四邻居像素的差异,这种性质通常被用来当做图像上的边缘检测算子。
同理,在图信号中,拉普拉斯算子也被用来描述中心节点与邻居节点之间的信号的差异
L
x
=
(
D
−
A
)
x
=
[
⋅
⋅
⋅
,
∑
v
j
∈
N
(
v
i
)
(
x
i
−
x
j
)
,
⋅
⋅
⋅
]
Lx=(D-A)x=\bigg[···,\sum_{v_j∈N(v_i)}(x_i-x_j),···\bigg]
Lx=(D−A)x=[⋅⋅⋅,vj∈N(vi)∑(xi−xj),⋅⋅⋅]
由此可知,拉普拉斯矩阵是一个反映图信号局部平滑度的算子。更进一步来说,拉普拉斯矩阵可以让我们定义一个非常重要的二次型:
x
T
L
x
=
∑
v
i
∑
v
j
∈
N
(
v
i
)
x
i
(
x
i
−
x
j
)
=
∑
e
i
j
∈
E
(
x
i
−
x
j
)
2
x^TLx=\sum_{v_i}\sum_{v_j∈N(v_i)}x_i(x_i-x_j)=\sum_{e_{ij}∈E}(x_i-x_j)^2
xTLx=vi∑vj∈N(vi)∑xi(xi−xj)=eij∈E∑(xi−xj)2
令
T
V
(
x
)
=
x
T
L
x
=
∑
e
i
j
∈
E
(
x
i
−
x
j
)
2
TV(x)=x^TLx=\sum_{e_{ij}∈E}(x_i-x_j)^2
TV(x)=xTLx=∑eij∈E(xi−xj)2,称
T
V
(
x
)
TV(x)
TV(x)为图信号的总变差(Total Variation)。总变差是一个标量,它将各条边上信号的差值进行加和,刻画了图信号整体的平滑度。
图傅里叶变换
图信号傅里叶变换的定义:将图信号由空域视角转化到频域视角,便于图信号处理理论体系的建立。
假设图G的拉普拉斯矩阵为 L ∈ R N × N L∈R^{N×N} L∈RN×N,由于L是一个实对称矩阵,根据实对称矩阵都可以被正交对角化,可得 L = V ∧ V T L=V∧V^T L=V∧VT。 V ∈ R N × N V∈R^{N×N} V∈RN×N是一个正交矩阵,即 V V T = I VV^T=I VVT=I。 V = [ v 1 , v 2 , ⋅ ⋅ ⋅ , v N ] V=[v_1,v_2,···,v_N] V=[v1,v2,⋅⋅⋅,vN]表示L的N个特征向量,由于V是一个正交矩阵,这些特征向量都是彼此之间线性无关的单位向量。 λ k \lambda _k λk表示第k个特征向量对应的特征值,对特征值进行升序排列,即 λ 1 ≤ λ 2 ≤ ⋅ ⋅ ⋅ ≤ λ N \lambda _1 \leq\; \lambda2 \leq\;··· \leq\; \lambda_N λ1≤λ2≤⋅⋅⋅≤λN。
对于任意给定的向量x,拉普拉斯矩阵的二次型: x T L x = ∑ e i j ∈ E ( x i − x j ) 2 ≥ 0 x^TLx=\sum_{e_{ij}∈E}(x_i-x_j)^2 \geq\; 0 xTLx=∑eij∈E(xi−xj)2≥0,因此拉普拉斯矩阵是一个半正定型矩阵,其所有的特征值均大于等于0。 L I = 0 LI=0 LI=0,拉普拉斯矩阵具有最小的特征值0,即 λ 1 = 0 \lambda _1 = 0 λ1=0。另外可以证明,对于 L s y m L_{sym} Lsym,其特征值存在一个上限: λ N ≤ 2 \lambda _N \leq\; 2 λN≤2。
图傅里叶变换(Graph Fourier Transform,GFT):对于任意一个在图G上的信号x,其图傅里叶变换为:
x
~
k
=
∑
i
=
1
N
V
k
i
T
x
i
=
<
v
k
,
x
>
\widetilde{x}_k=\sum_{i=1}^NV_{ki}^Tx_i=<v_k,x>
x
k=i=1∑NVkiTxi=<vk,x>
称特征向量为傅里叶基,
x
~
k
\widetilde{x}_k
x
k是x在第k个傅里叶基上的傅里叶系数。从定义上看,傅里叶系数本质上是图信号在傅里叶基上的投影,衡量了图信号与傅里叶基之间的相似度。用矩阵形式可以计算出所有的傅里叶系数:
x
~
=
V
T
x
,
x
~
∈
R
N
\widetilde{x}=V^Tx, \widetilde{x}∈R^N
x
=VTx,x
∈RN
由于V是一个正交矩阵,对于上式左乘V,则:
V
x
~
=
V
V
T
x
=
I
x
=
x
V\widetilde{x}=VV^Tx=Ix=x
Vx
=VVTx=Ix=x,即
x
=
V
x
~
,
x
∈
R
N
x=V\widetilde{x},x∈R^N
x=Vx
,x∈RN
于是可以将逆图傅里叶变换(Inverse Graph Fourier Transform,IGFT)定义为
x
k
=
∑
i
=
1
N
V
k
i
⋅
x
~
i
x_k=\sum_{i=1}^NV_{ki}·\widetilde{x}_i
xk=i=1∑NVki⋅x
i
式
x
=
V
x
~
,
x
∈
R
N
x=V\widetilde{x},x∈R^N
x=Vx
,x∈RN是一种矩阵形式的逆图傅里叶变换,将其展开成向量形式有:
x
=
V
x
~
=
∑
k
=
1
N
x
~
k
v
k
x=V\widetilde{x}=\sum_{k=1}^N\widetilde{x}_kv_k
x=Vx
=k=1∑Nx
kvk
由此可知,从线性代数的角度来看,
v
1
,
v
2
,
⋅
⋅
⋅
,
v
N
v_1,v_2,···,v_N
v1,v2,⋅⋅⋅,vN组成了N维特征空间中的一组完备的基向量,图G上的任意一个图信号都可以被表征成这些基向量的线型加权。具体来说,权重就是图信号在对应傅里叶基上的傅里叶系数。
对总变差公式进行改写
T
V
(
x
)
=
x
T
L
x
=
x
T
V
∧
V
T
x
,
代
入
x
=
V
x
~
,
得
T
V
(
x
)
=
x
~
∧
x
~
=
∑
i
=
1
N
λ
k
x
~
k
2
TV(x)=x^TLx=x^TV∧V^Tx,代入x=V\widetilde{x},得\\ TV(x)=\widetilde{x}∧\widetilde{x}=\sum_{i=1}^N\lambda _k \widetilde{x}_k^2
TV(x)=xTLx=xTV∧VTx,代入x=Vx
,得TV(x)=x
∧x
=i=1∑Nλkx
k2
从上式可以看出,图信号的总变差与图的特征值之间有着非常直接的线性对应关系,总变差是图的所有特征值的一个线性组合,权重是图信号相对应的傅里叶系数的平方。
图信号的能量:
E
(
x
)
=
∣
∣
x
∣
∣
2
2
=
x
T
x
=
(
V
x
~
)
T
(
V
x
~
)
=
x
~
T
x
~
E(x)=||x||_2^2=x^Tx=(V\widetilde{x})^T(V\widetilde{x})=\widetilde{x}^T\widetilde{x}
E(x)=∣∣x∣∣22=xTx=(Vx
)T(Vx
)=x
Tx
即图信号的能量可以同时从空域和频域进行等价定义。单位向量的图信号能量为1。
图滤波器
图滤波器(Graph Filter)定义为:对给定图信号的频谱中各个频率分量的强度进行增强或者衰减的操作。假设图滤波器为
H
∈
R
N
×
N
,
H
:
R
N
→
R
N
H∈R^{N×N},H:R^N→R^N
H∈RN×N,H:RN→RN,令输出图信号为y,则:
y
=
H
x
=
∑
k
=
1
N
(
h
(
λ
k
)
x
~
k
)
v
k
y=Hx=\sum_{k=1}^N(h(\lambda _k)\widetilde{x}_k)v_k
y=Hx=k=1∑N(h(λk)x
k)vk
此式中增强还是衰减是通过
h
(
λ
)
h(\lambda)
h(λ)项来控制的。
化简可得:
H
=
V
[
h
(
λ
1
)
h
(
λ
2
)
⋱
h
(
λ
N
)
]
V
T
=
V
∧
h
V
T
H=V \begin{bmatrix} h(\lambda_1) \\ \quad & h(\lambda_2) \\ \quad & \quad & \ddots\\ \quad & \quad & \quad & h(\lambda_N) \end{bmatrix} V^T=V∧_hV^T
H=V⎣⎢⎢⎡h(λ1)h(λ2)⋱h(λN)⎦⎥⎥⎤VT=V∧hVT
相较于拉普拉斯矩阵,H仅仅改动了对角矩阵上的值,因此,H具有以下形式:
H
i
j
=
0
H_{ij}=0
Hij=0,如果
i
≠
j
或
者
e
i
j
∉
E
i≠j或者e_{ij}∉E
i=j或者eij∈/E。也就是说,H矩阵只在对角与边坐标上时才有可能取非零值。从算子的角度来看,
H
x
Hx
Hx描述了一种作用在每个节点一阶子图上的变换操作。一般来说,我们称满足上述性质的矩阵为G的图位移算子(Graph Shift Operator)。
图滤波器具有以下性质:
- 线性: H ( x + y ) = H x + H y H(x+y)=Hx+Hy H(x+y)=Hx+Hy
- 滤波操作是线性无关的: H 1 ( H 2 x ) = H 2 ( H 1 x ) H_1(H_2x)=H_2(H_1x) H1(H2x)=H2(H1x)
- 如果 h ( λ ) ≠ 0 h(\lambda)≠0 h(λ)=0,则该滤波操作是可逆的
称 ∧ h ∧_h ∧h为图滤波器H的频率响应矩阵,对应的函数 h ( λ ) h(\lambda) h(λ)为H的频率响应函数,不同的频率响应函数可以实现不同的滤波效果。常见的滤波器有:低通滤波器,高通滤波器,带通滤波器。
空域角度
对于
y
=
H
x
=
∑
k
=
0
K
h
k
L
k
x
y=Hx=\sum_{k=0}^Kh_kL^kx
y=Hx=∑k=0KhkLkx,如果设定
x
(
k
)
=
L
k
x
=
L
x
(
k
−
1
)
x^{(k)}=L^kx=Lx^{(k-1)}
x(k)=Lkx=Lx(k−1),则
y
=
∑
k
=
0
K
h
k
x
(
k
)
y=\sum_{k=0}^Kh_kx^{(k)}
y=k=0∑Khkx(k)
通过上式,将输出图信号变成了(K+1)组图信号的线型加权。
x
(
k
)
x^{(k)}
x(k)的计算只需要所有节点的k阶邻居参与,称这种性质为图滤波器的局部性。
从空域角度来看,滤波操作具有以下性质:
- 具有局部性,每个节点的输出信号只需要考虑其K阶子图;
- 可通过K步迭代式的矩阵向量乘法来完成滤波操作。
频域角度
将
L
=
V
∧
V
T
L=V∧V^T
L=V∧VT代入
H
=
∑
k
=
0
K
h
k
L
k
H=\sum_{k=0}^Kh_kL^k
H=∑k=0KhkLk得
V
(
∑
k
=
0
K
h
k
∧
k
)
V
T
=
V
[
∑
k
=
0
K
h
k
λ
1
k
⋱
∑
k
=
0
K
h
k
λ
N
k
]
V
T
V\bigg( \sum_{k=0}^Kh_k∧^k \bigg)V^T=V \begin{bmatrix} \sum_{k=0}^Kh_k\lambda_1^k \\ \quad & \ddots \\ \quad & \quad & \sum_{k=0}^Kh_k\lambda_N^k \end{bmatrix} V^T
V(k=0∑Khk∧k)VT=V⎣⎡∑k=0Khkλ1k⋱∑k=0KhkλNk⎦⎤VT
由上式可看出H的频率响应函数为
λ
\lambda
λ的K次代数多项式,如果K足够大,我们可以用这种形式去逼近任意一个关于
λ
\lambda
λ的函数。
如果我们用该滤波器进行滤波,则:
y
=
H
x
=
V
(
∑
k
=
1
K
h
k
∧
k
)
V
T
x
y=Hx=V\bigg( \sum_{k=1}^Kh_k∧^k \bigg)V^Tx
y=Hx=V(k=1∑Khk∧k)VTx
从频域角度来看,图滤波器有以下性质:
- 从频域角度能够更加清晰地完成对图信号的特定滤波操作;
- 图滤波器如何设计具有显式的公式指导(???)
- 对矩阵进行特征分解是一个非常耗时的操作,具有 O ( N 3 ) O(N^3) O(N3)的时间复杂度,相比空域视角中的矩阵向量乘法而言,有工程上的局限性。
图卷积神经网络
给定两组G上的图信号
x
1
、
x
2
x_1、x_2
x1、x2,其图卷积运算定义如下:
x
1
∗
x
2
=
I
G
F
T
(
G
F
T
(
x
1
)
⊙
G
F
T
(
x
2
)
)
,
其
中
⊙
表
示
哈
达
玛
积
x
1
∗
x
2
=
V
(
(
V
T
x
1
)
⊙
(
V
T
x
2
)
)
=
V
(
x
~
1
⊙
(
V
T
x
2
)
)
=
V
(
d
i
a
g
(
x
~
1
)
(
V
T
x
2
)
)
=
(
V
d
i
a
g
(
x
~
1
)
V
T
)
x
2
x_1*x_2=IGFT(GFT(x_1)⊙GFT(x_2)),其中⊙表示哈达玛积\\ x_1*x_2=V((V^Tx_1)⊙(V^Tx_2))=V(\widetilde{x}_1⊙(V^Tx_2))\\ =V(diag(\widetilde{x}_1)(V^Tx_2))=(Vdiag(\widetilde{x}_1)V^T)x_2
x1∗x2=IGFT(GFT(x1)⊙GFT(x2)),其中⊙表示哈达玛积x1∗x2=V((VTx1)⊙(VTx2))=V(x
1⊙(VTx2))=V(diag(x
1)(VTx2))=(Vdiag(x
1)VT)x2
由上式可知,两组图信号的图卷积运算总能转化为对应形式的图滤波运算,从这个层面上来看,图卷积等价于图滤波。
1.对频率响应矩阵进行参数化
对频率响应矩阵进行参数化,可定义如下神经网络层:
X
′
=
σ
(
V
d
i
a
g
(
θ
)
V
T
X
)
=
σ
(
Θ
X
)
X'=\sigma(Vdiag(\theta)V^TX)=\sigma(\Theta X)
X′=σ(Vdiag(θ)VTX)=σ(ΘX)
其中
σ
(
⋅
)
\sigma(·)
σ(⋅)是激活函数,
θ
=
[
θ
1
,
θ
2
,
⋅
⋅
⋅
,
θ
N
]
\theta=[\theta_1,\theta_2,···,\theta_N]
θ=[θ1,θ2,⋅⋅⋅,θN]是需要学习的参数,
Θ
\Theta
Θ是对应的需要学习的图滤波器,X是输入的图信号矩阵,X’是输出的图信号矩阵。
引入参数过多极易发生过拟合。
2.对多项式系数进行参数化
同样,为了拟合任意的频率响应函数,也可以将拉帕拉斯矩阵的多项式形式转化为一种可学习的形式:
X
′
=
σ
(
V
(
∑
k
=
0
K
θ
k
∧
k
)
V
T
X
)
=
σ
(
V
d
i
a
g
(
Ψ
θ
)
V
T
X
)
X'=\sigma \Big(V \Big(\sum_{k=0}^K\theta_k∧^k \Big)V^TX \Big)=\sigma(Vdiag(\Psi\theta)V^TX)
X′=σ(V(k=0∑Kθk∧k)VTX)=σ(Vdiag(Ψθ)VTX)
其中
θ
=
[
θ
1
,
θ
2
,
⋅
⋅
⋅
,
θ
N
]
\theta=[\theta_1,\theta_2,···,\theta_N]
θ=[θ1,θ2,⋅⋅⋅,θN]是多项式系数向量,也是该网络层真正需要学习的参数,参数量K可自由控制。K的大小决定了可拟合频率响应函数的次数高低。一般来说,
K
<
<
N
K<<N
K<<N,这样大大降低了模型过拟合的风险。
3.设计固定的图滤波器
上述两种方法虽然降低了参数量,但矩阵特征分解复杂度较高。在此,设置K=1,则:
X
′
=
σ
(
θ
0
X
+
θ
1
L
X
)
令
θ
0
=
θ
1
=
θ
,
则
有
X
′
=
σ
(
θ
(
I
+
L
)
X
)
=
σ
(
θ
L
~
X
)
X'=\sigma(\theta_0X+\theta_1LX) \quad 令\theta_0=\theta_1=\theta,则有\\ X'=\sigma(\theta(I+L)X)=\sigma(\theta\widetilde{L}X)
X′=σ(θ0X+θ1LX)令θ0=θ1=θ,则有X′=σ(θ(I+L)X)=σ(θL
X)
这里的θ是一个标量,相当于对
L
~
\widetilde{L}
L
做尺度变换,这种变换在神经网络中会被归一化替代,所以参数θ是不必要引入,设置
θ
=
1
\theta=1
θ=1,就得到了一个固定的图滤波器
L
~
\widetilde{L}
L
。
GCN实战
使用数据集为Cora数据集,该数据集由2708篇论文,5429条引用关系组成。这些论文被分为类。每篇论文的特征由词袋模型得到,特征维度为1433,分别用0或者1代表有无。
~
GCN层定义
class GraphConvolution(nn.Module):
def __init__(self, input_dim, output_dim, use_bias=True):
"""图卷积:L*X*\theta
Args:
----------
input_dim: int
节点输入特征的维度
output_dim: int
输出特征维度
use_bias : bool, optional
是否使用偏置
"""
super(GraphConvolution, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.use_bias = use_bias
self.weight = nn.Parameter(torch.Tensor(input_dim, output_dim))
if self.use_bias:
self.bias = nn.Parameter(torch.Tensor(output_dim))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self):
init.kaiming_uniform_(self.weight)
if self.use_bias:
init.zeros_(self.bias)
def forward(self, adjacency, input_feature):
"""邻接矩阵是稀疏矩阵,因此在计算时使用稀疏矩阵乘法
Args:
-------
adjacency: torch.sparse.FloatTensor
邻接矩阵
input_feature: torch.Tensor
输入特征
"""
support = torch.mm(input_feature, self.weight)
output = torch.sparse.mm(adjacency, support)
if self.use_bias:
output += self.bias
return output
~
两层GCN模型
class GcnNet(nn.Module):
"""
定义一个包含两层GraphConvolution的模型
"""
def __init__(self, input_dim=1433):
super(GcnNet, self).__init__()
self.gcn1 = GraphConvolution(input_dim, 16)
self.gcn2 = GraphConvolution(16, 7)
def forward(self, adjacency, feature):
h = F.relu(self.gcn1(adjacency, feature))
logits = self.gcn2(adjacency, h)
return logits
······
模型训练与测试
# 训练主体函数
def train():
loss_history = []
val_acc_history = []
model.train()
train_y = tensor_y[tensor_train_mask]
for epoch in range(EPOCHS):
logits = model(tensor_adjacency, tensor_x) # 前向传播
train_mask_logits = logits[tensor_train_mask] # 只选择训练节点进行监督
loss = criterion(train_mask_logits, train_y) # 计算损失值
optimizer.zero_grad()
loss.backward() # 反向传播计算参数的梯度
optimizer.step() # 使用优化方法进行梯度更新
train_acc, _, _ = test(tensor_train_mask) # 计算当前模型训练集上的准确率
val_acc, _, _ = test(tensor_val_mask) # 计算当前模型在验证集上的准确率
# 记录训练过程中损失值和准确率的变化,用于画图
loss_history.append(loss.item())
val_acc_history.append(val_acc.item())
print("Epoch {:03d}: Loss {:.4f}, TrainAcc {:.4}, ValAcc {:.4f}".format(
epoch, loss.item(), train_acc.item(), val_acc.item()))
return loss_history, val_acc_history
······
完整代码见《深入浅出图神经网络》官网github链接>chapter05,注意测试中可能会遇到以下问题:
1、数据集加载问题数据集cora需要自己下载,网址为:cora数据集下载>/data/…
路径需要自己配置,data_root
class CoraData: def __init__(self, data_root="data/cora", rebuild=False):2.from sklearn.manifold import TSNE,导入sklearn测试时报错
报错类似DeprecationWarning:
np.floatis a deprecated alias for the builtinfloat. To silence this warning, use float by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, usenp.float64here.Deprecated in NumPy 1.20;
解决方案:将报错
sklearn中对应位置处np.float修改为np.float64
运行结果如下:
Using Cached file: data/cora\ch5_cached.pkl
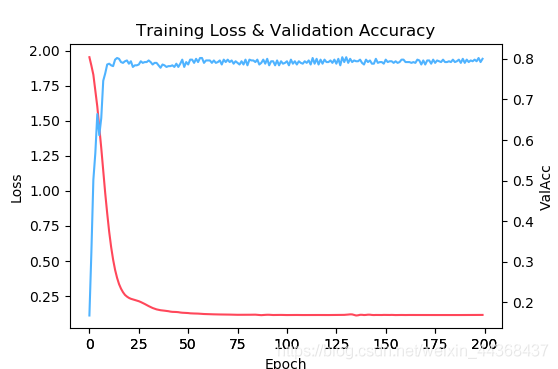
Epoch 000: Loss 1.9530, TrainAcc 0.2429, ValAcc 0.1680
Epoch 001: Loss 1.8931, TrainAcc 0.4929, ValAcc 0.3240
Epoch 002: Loss 1.8281, TrainAcc 0.6857, ValAcc 0.5020
···
Epoch 197: Loss 0.1153, TrainAcc 1.0, ValAcc 0.8020
Epoch 198: Loss 0.1155, TrainAcc 1.0, ValAcc 0.7920
Epoch 199: Loss 0.1156, TrainAcc 1.0, ValAcc 0.8000
Test accuarcy: 0.8040000200271606
损失值和准确率的变化趋势可视化
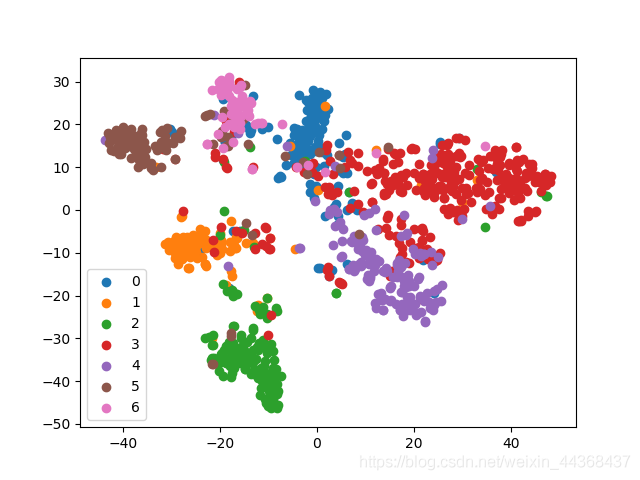
将最后一层输出结果进行TSNE降维可视化
参考资料:
《深入浅出图神经网络》GNN原理解析
cora数据集:https://github.com/kimiyoung/planetoid/tree/master
GCN官方完整代码:https://github.com/FighterLYL/GraphNeuralNetwork
没有机器学习和深度学习的经验学这个还是很吃力,最难的地方是代码方面,涉及太广了…
加油,会慢慢熬出来的😶