【数据结构】第一章——绪论(2)
算法和算法评价

前言
大家好,很高兴又和大家见面啦!!!今天我们将继续介绍数据结构第一章的相关内容。
在上一篇中,我们介绍了数据结构的基本概率,简单说明了一下数据结构的三要素——数据的逻辑结构、数据的存储结构以及数据的运算。我个人是感觉这些定义有点不好理解,不过没关系,这些内容会随着我们学习的深入而不断提升对它们的理解。下面我们就来看一下第一章的第二部分内容——算法和算法评价。
算法的基本概念
定义
算法(Algorithm)是对特定问题求解步骤的一种描述,它是指令的有限序列,其中的每条指令表示一个或多个操作。
理解定义
对于这个定义我是这样理解的——在C语言中,我们有介绍过函数,在我们用函数编写一个功能时,函数的返回类型、函数名和函数的参数都是在对这个函数进行声明,函数的具体实现是在函数体内完成的,这个实现的过程,我们就可以简单的理解为是算法。下面我举一个最简单的算法:
//实现打印hello
int main()
{
printf("hello\n");
return 0;
}
现在我为了实现打印hello这个功能,我在主函数体内通过调用库函数printf完成了这个功能,那我现在就可以称这个实现这个功能的过程就是实现这个功能的算法。
在这个算法中,它有2个指令——printf和return;
对于这两条指令,它都只有一个操作——打印和返回0;
算法的5个特性
那我们现在对算法有了一个初步的了解之后,我们现在来看一下算法又有哪些特性;
有穷性
定义
一个算法必须总在执行有穷步之后结束,且每一步都可在有穷时间内完成。
理解
对于有穷性的理解,我的理解就是像死循环这种无法结束的代码就称不上是算法,如下图所示:

对于这个循环来说,判断条件为1,结果恒为真,代码进入死循环,不断的打印hello,像这种打印的实现就称不上是算法,但是如果我们将它简单修改一下,如下图所示:
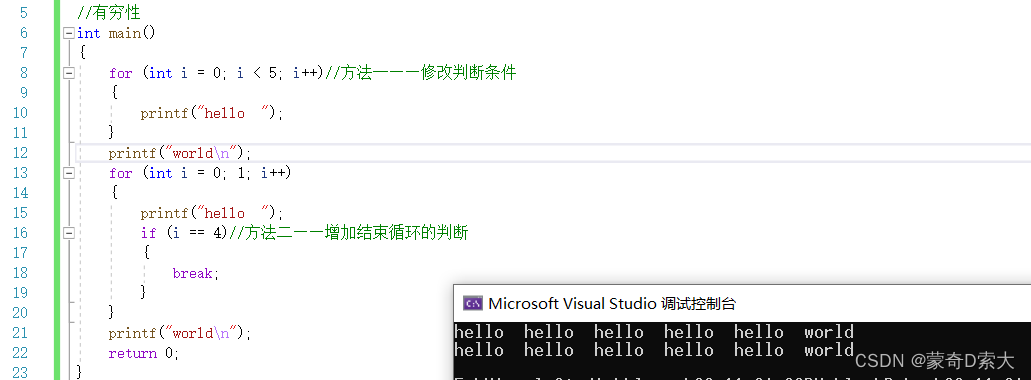
可以看到,我们不管是修改了判断条件也好,还是增加了介绍标志也好,都是在告诉计算机,你现在需要在什么时候停止,等计算机运行到那个停止点时,它就停止不再运行了。也就是说有穷性就是程序能够正常的终止。
确定性
定义
算法中每条指令必须有确切的含义,对于相同的输入只能得到相同的输出。
理解
确定性的话我们可以理解为就像数学中的函数一样,自变量与因变量的关系可以是一对一也可以是多对一,但绝不能是一对多这种情况。下面我们来通过计算机语言来描述:
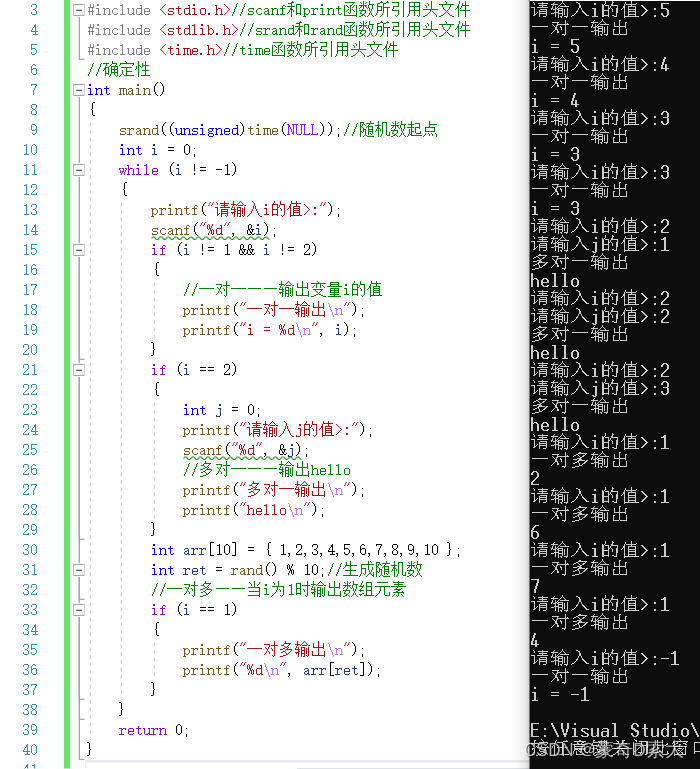
在这个代码中我们通过判断变量i的值是否为-1来决定是否要继续循环;
在循环中则进行了三个功能的实现——输出i的值、输出hello以及输出数组元素,对于个功能的实现如下:
- 当i的值不为1且i的值也不为2时,我们执行的是一对一的输出,可以看到结果展示每一个输入的值都能得到一个输出,并且同一个输入能得到同一个输出;
- 当i的值为2时,我们执行的是多对一的输出,这时需要输入第二个变量j,从结果中可以看到当满足i==2这个条件时,不管j的值为多少,我们都能得到hello的打印结果;
- 当i的值为1时,我们执行的是一对多的输出,我们通过rand函数与srand函数生成随机数使数组的下标随机,在这种情况下同一个i值得到的结果却是截然不同的;
我们现在从算法确定性的角度来分析,那么对于输出数组元素这个内容的实现显然就不满足算法的确定性;
为了实现输出数组元素的功能,我们可以如下进行代码编写:
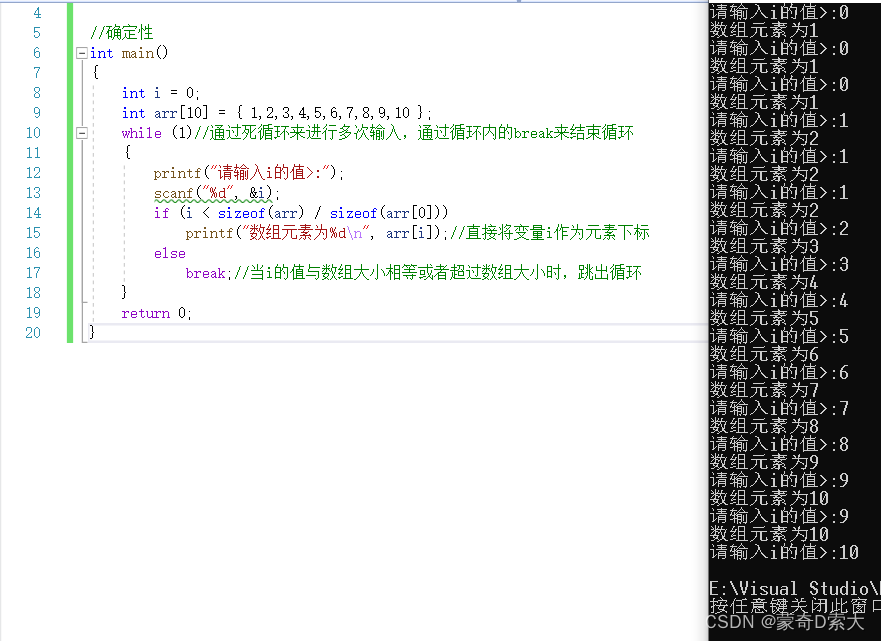
像这样编写代码后我们可以看到,对于变量i的每一次输入,我们都能得到一个输出,并且同样的输入对应的是同样的输出,不同的输入对应的是不同的输出,此时输入与输出满足一对一的关系;
对于上述这种输入和输出满足一对一关系或者多对一关系的代码,我们就称这样的算法是具有确定性的;
可行性
定义
算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
理解
对于可行性我的理解是——我们在算法中的操作过程,都是能够通过计算机语言进行实现的。
如我想打印内容,我可以通过库函数printf、putchar等等这样的输出函数进行打印;
我想输入数据我可以通过scanf、gets等这样的输入函数进行数据的输入;
我想进行加减乘除的运算我可以通过+-*/这些算术操作符实现;
除了上述这些内容外,只要是我们想实现的功能,都是能够通过相应的计算机语言进行实现的,这就是可行性;
输入
定义
一个算法有零个或多个输入,这些输入取自于某个特定的对象的集合。
理解
对于一个算法而言,我们可以没有输入,如通过printf在屏幕上输出hello world:
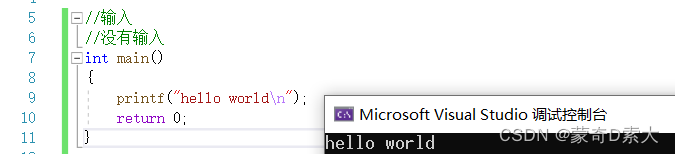
我们也可以只有一个输入,如通过输入给变量a赋值,并在屏幕上以a=%d的形式输出a的值:
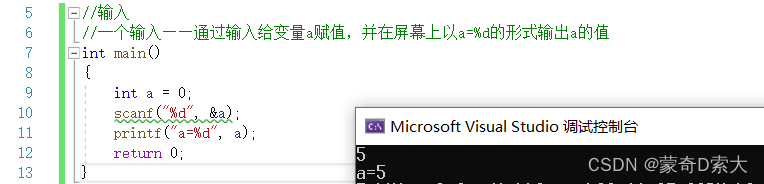
我们还可以有多个输入,如编写一个简单的进行两个数的四则运算的程序:
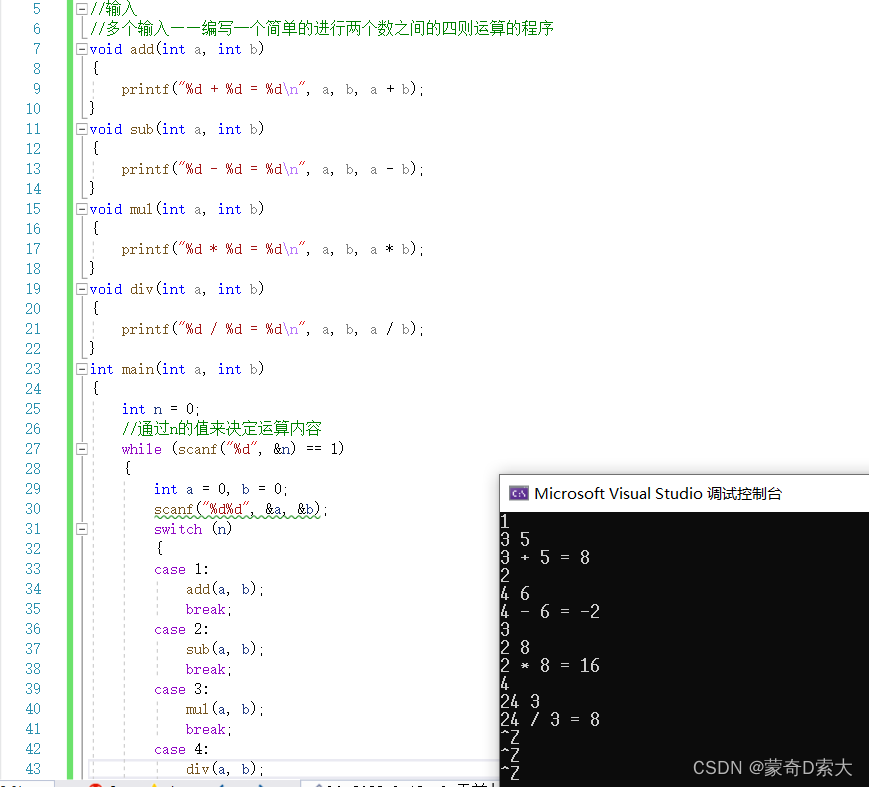
从上述例子中我们可以进一步验证这个结论——在一个算法中,可以没有输入,也可以有一个或多个输入;
输出
定义
一个算法有一个或多个输出,这些输出是与输入有着某种特定关系的量。
理解
从前面的举例中我们可以看到,不管是最简单的算法——打印hello world也好,还是能够完成四则运算功能的算法也好,它们都有一个共同点——至少有一个输出。
也就是说,对一个算法而言,至少要有一个输出,并且如果有输入的话,这些输出是与输入之间存在某种特定关系的;
如上述的四则运算,每一个输出都与输入有一个特定的关系:
在加法中,输出的值是输入值的和;
在减法中,输出的值是输入值的差;
在乘法中,输出的值是输入值的积;
在除法中,输出的值是输入值的商;
和、差、积、商这些就是输入与输出之间的特定关系;
什么是好的算法
现在我们已经了解了算法的五个特性,那么对一个算法而言,什么样的算法才称的上是好的算法呢?
通常情况下,一个好的算法需要达到以下几个目标——正确性、可读性、健壮性、高效率与低存储量需求。
这些目标分别是代表什么意思呢?下面我们一起来了解一下
正确性
定义
算法应能够正确地解决求解问题。
理解
对于一个算法来说,它应该能正确的来解决问题,就比如我想计算1+1,那这个算法就不能求解的是1*1;
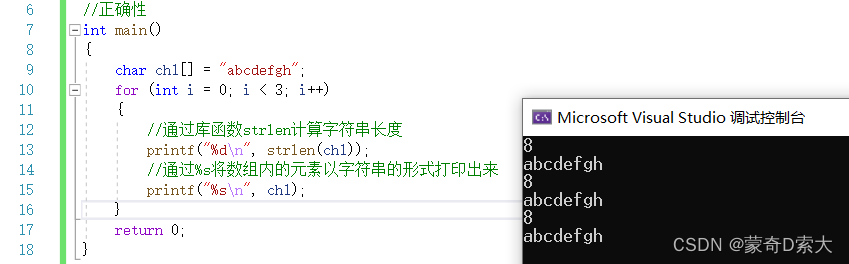
对于这个算法而言,我们可以看到输出的结果是确定的,我们很好的实现了计算字符串的长度,并将字符串给打印出来,这个算法正确的解决了我们的问题;
可读性
定义
算法应具有良好的可读性,以帮助人们理解。
理解
对于一个好的算法,能够让大家很好的理解每一句代码的含义,比如我要实现两个整数的互换:
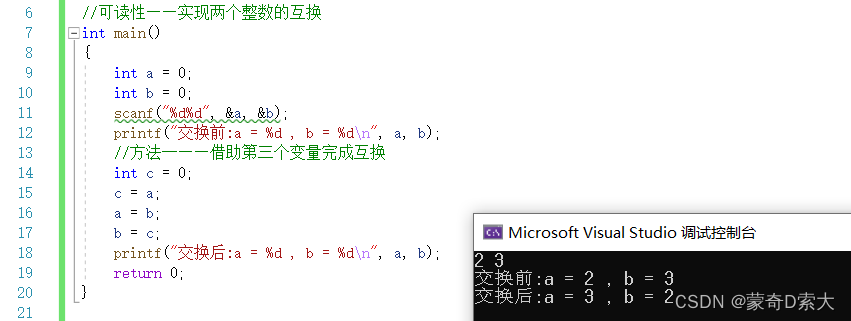
在这个代码中我们很容易理解每一句代码的含义,我们在进行输入后,第一次输出的值就是我们输入的值,我们通过第三个变量c来将变量a和b的值进行了互换,之后我们将交换后的值进行了输出。
但是如果我通过下面这种方式来实现的话:
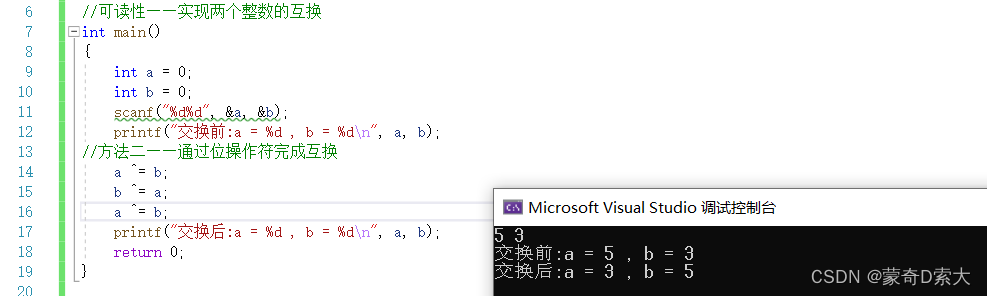
可以看到,通过位操作符的方式,我们同样可以实现两个整数的互换,但是对于14-16这三行代码来说就不是那么容易理解了,这种方法相比于第一种方法来说,它的可读性就比较差,
健壮性
定义
输入非法数据时,算法能适当地做出反应或进行处理,而不会产生莫名其妙的输出结果。
理解
对于健壮性,我们可以通过switch语句来进行理解:
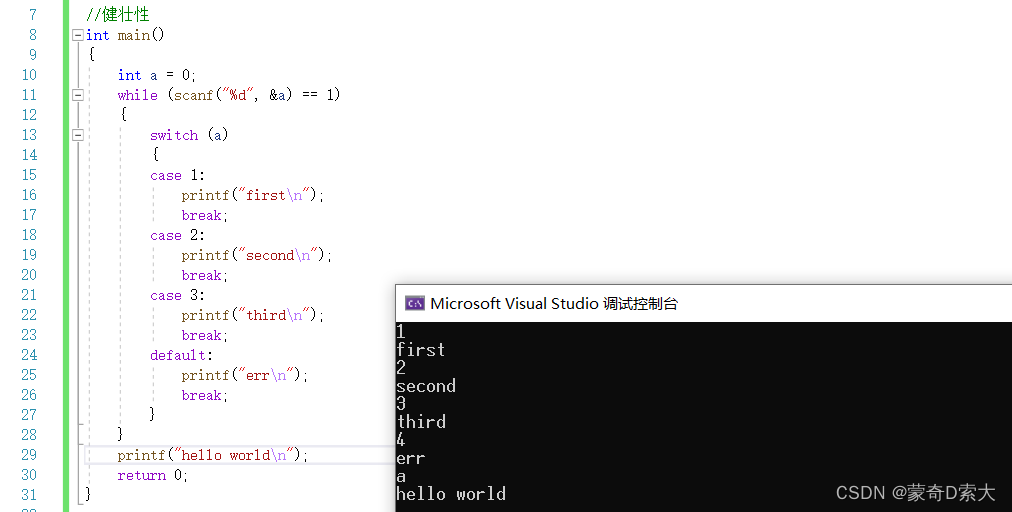
在这个代码中,我们通过多组输入的方式来进行连续的输入,如果输入的值都为整型,则可以进入循环执行分支语句,但是当输入的值不是整型时,则结束循环打印hello world;
在switch语句中我们可以通过整型变量的值来进入不同的分支,执行不同的语句,当a的值为1/2/3的任意一个值时,都能打印数字对于的英文次序,当a值为其它值时,则打印err;
不管是循环也好,还是switch语句也好,都能够对输入的非法数据做出反应,这个就是算法的健壮性,也就是算法不会因为输入非法数据而给出一个莫名其妙的结果;
高效率和低存储量需求
定义
效率指的是算法执行的时间,存储量需求是指算法执行过程中所需要的最大存储空间,这两者都与问题的规模有关。
理解
高效率指的就是算法执行的时间要少,低存储量需求就是算法执行的时候不会占用特别大的内存空间,我们可以通过下面的例子来简单的理解一下:
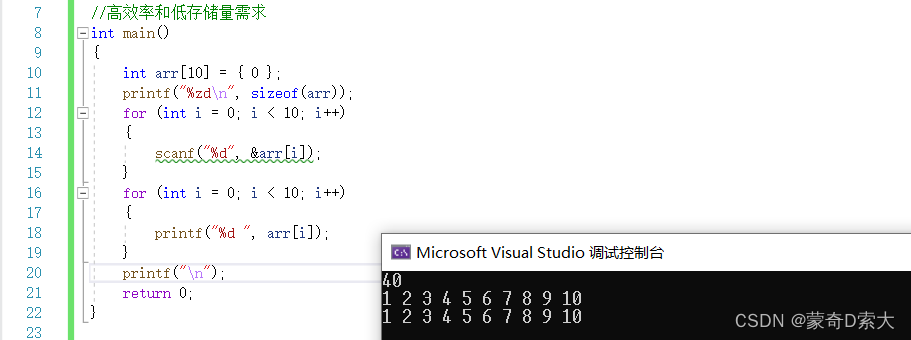
在这个例子中我们创建了一个一维整型数组,数组所占空间大小为40个字节;
如果每行代码执行时间为1ms的话,那我们运行完这行代码就需要至少20ms的时间;
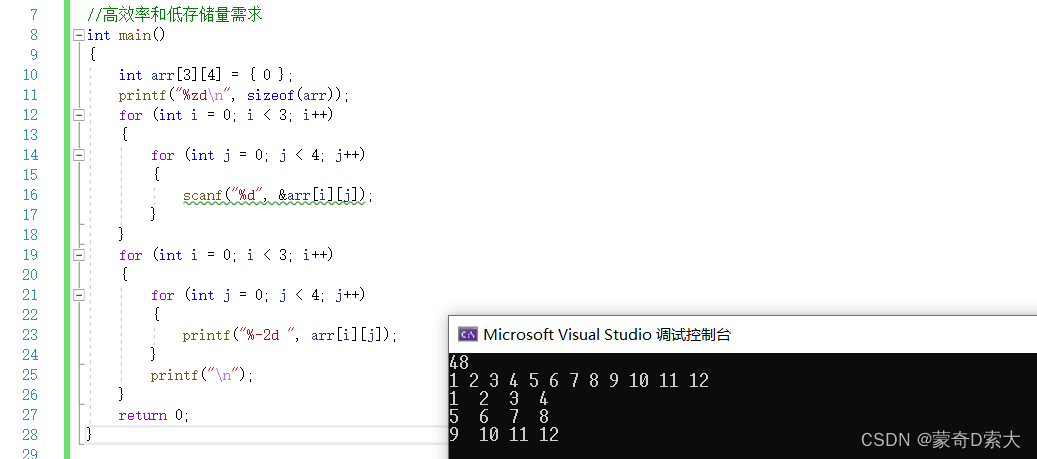
在这个例子中我们创建了一个二维整型数组,数组所占空间大小为48个字节;
如果每行代码执行时间为1ms的话,那我们运行完这行代码就需要至少24ms的时间;
从这两个例子当中我们可以看到,对于这两个算法而言,肯定是第一个算法要比第二个算法的效率更高,存储量需求更低。
所谓的高效率和低存储量需求我们可以简单的理解为——执行时间要少,占用空间内存要小;
下面有个问题需要我们来探讨一下,我们可以说第一个算法一定是比第二个算法要好吗?
这个问题我们先保留,在下一篇内容中我们将来好好探讨一下。
结语
在这一篇内容中我们介绍了三个内容:
- 什么是算法——实现一个功能的过程就是算法;
- 算法的五个特性——有穷性、确定性、可行性、输入和输出;
- 好的算法需要满足的五个目标——正确性、可读性、健壮性、高效率和低存储量需求;
内容不算很多,但是这些内容需要我们在接下来的学习中去好好的体会一下。我相信随着学习的不断深入,我们对这些内容肯定会有更加深刻的理解。
最后,感谢各位的翻阅,咱们下一篇再见!
【数据结构】第一章——绪论
【数据结构】第一章——绪论(1):【数据结构的基本概念】
- 本章内容介绍了数据结构的基本概念和术语以及数据结构的三要素
【数据结构】第一章——绪论(3):【时间复杂度】
- 本章详细介绍了算法的时间复杂度
【数据结构】第一章——绪论(4):【空间复杂度】
- 本章详细介绍了算法的空间复杂度
【数据结构】第一章——习题演练:【时间复杂度的分析方法与步骤】
- 本章详细介绍了算法的时间复杂度的分析方法与步骤