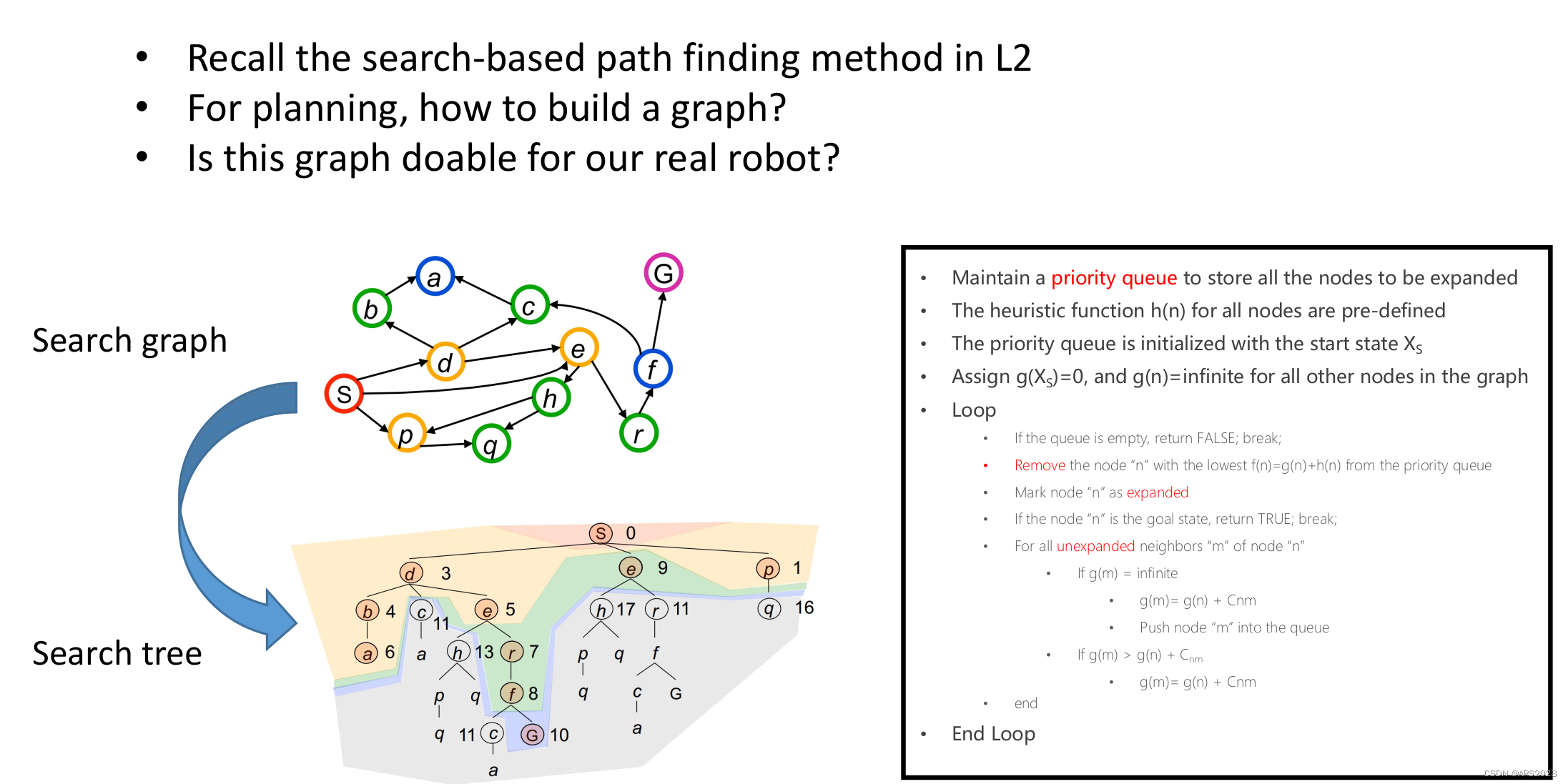
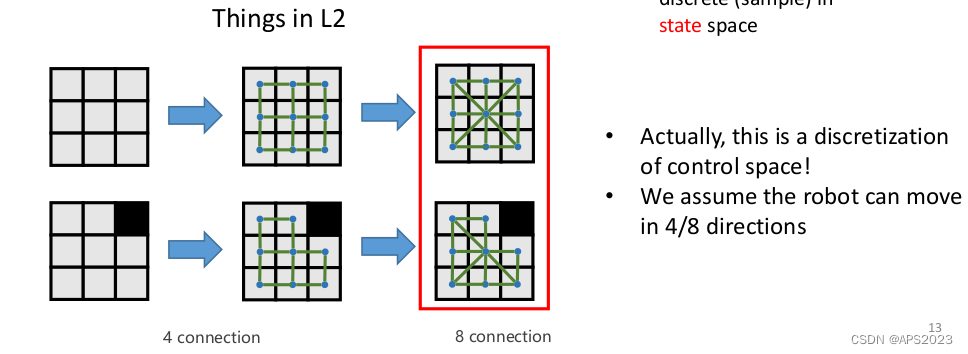
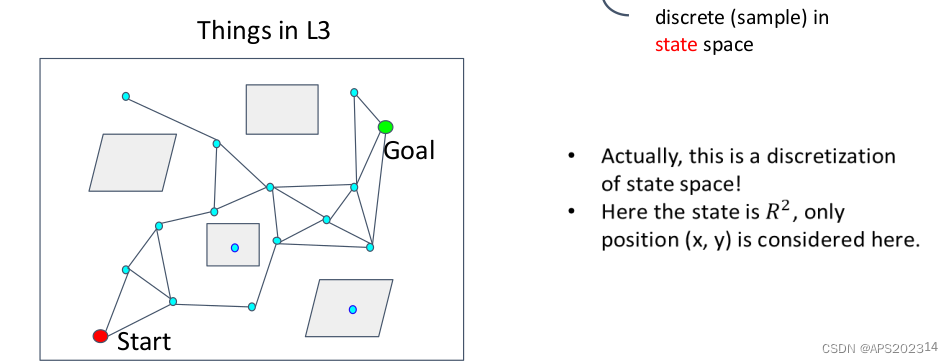
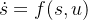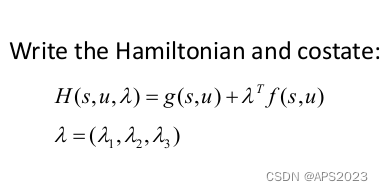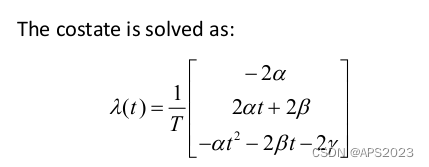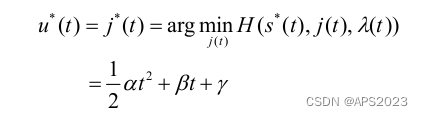移动机器人路径规划（四）--- 考虑机器人模型下的运动规划KINODYNAMIC PATHFINDING

目录

1 动力学概念简介

2 State Lattice Planning

3 Boundary Value Problem

4 混合A*算法 Hybrid A*

5 Kinodynamic RRT*

1 动力学概念简介

        一种生成机器人的运动同时受限制于运动学的约束（避障）以及动力学的约束（在速度加速度力的约束），既要保证运动的安全性（避障）还要保证微分的约束（力、加速度的约束）。

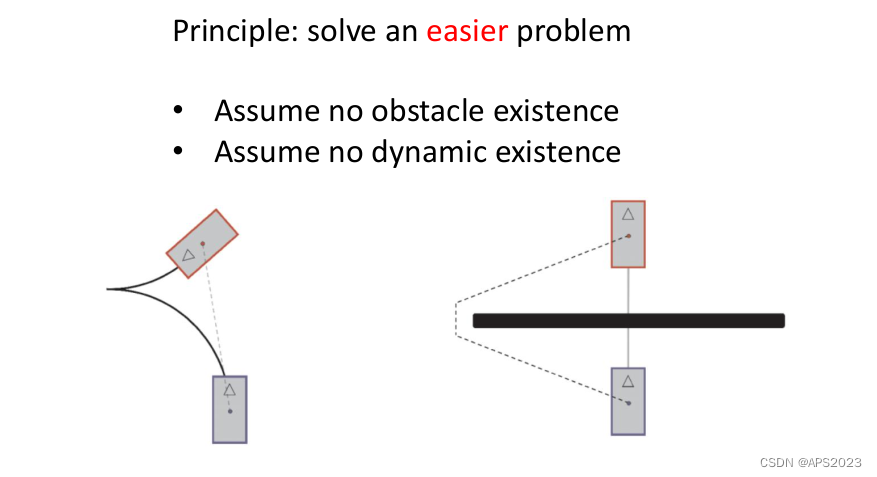
        真正的机器人是无法当作质点处理的。不可能像RRT*那样走直线的。

        做运动规划时也要考虑轨迹优化，而不单单在后端。（需要过渡，有个好的初值）。

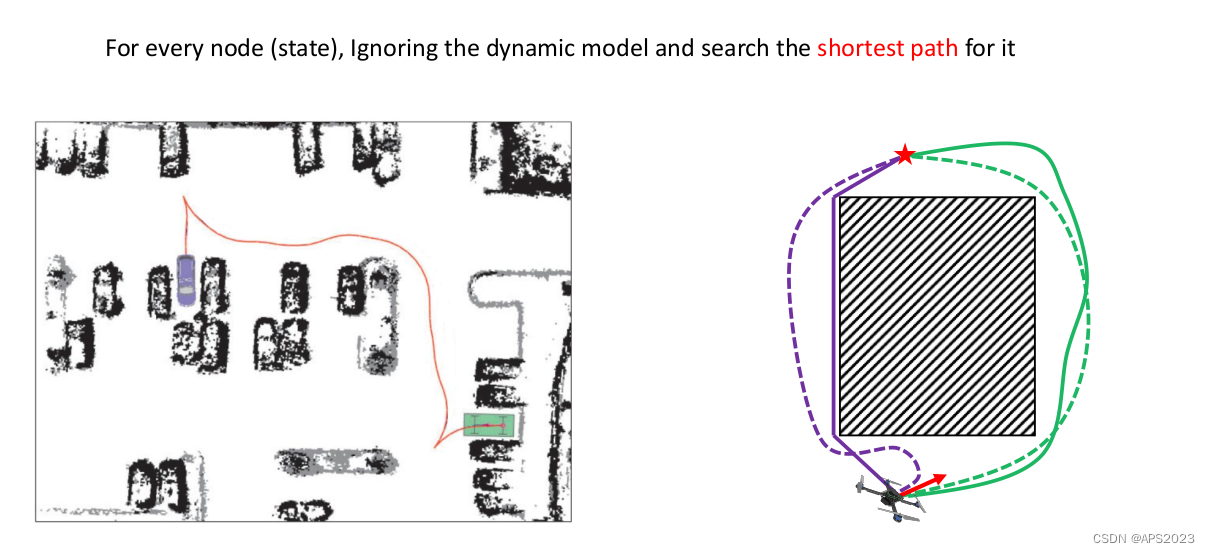
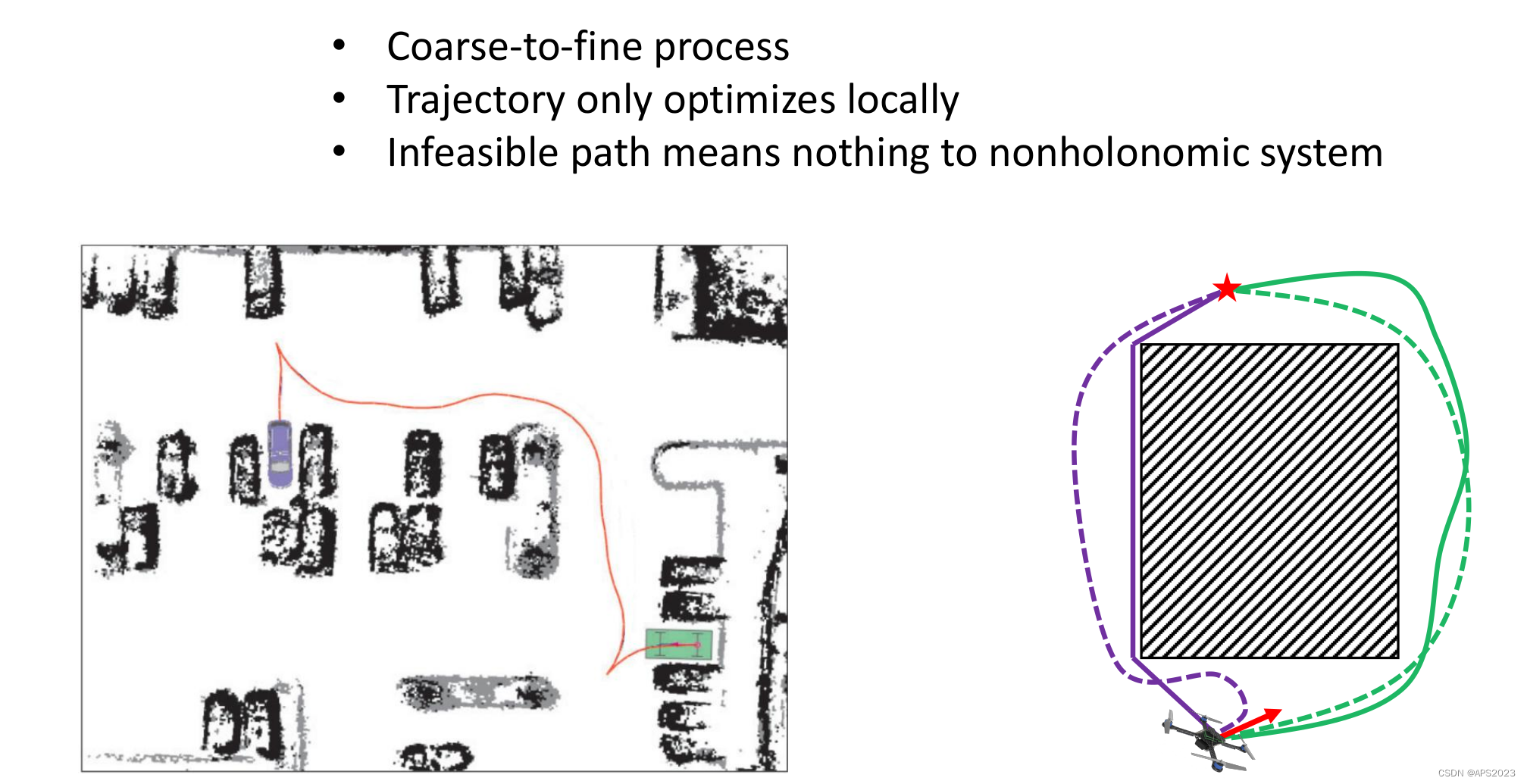
        并且很重要的，轨迹往往只能在局部被优化，看下面右面的紫色和绿色就可以。（虚线是优化过后的路径）

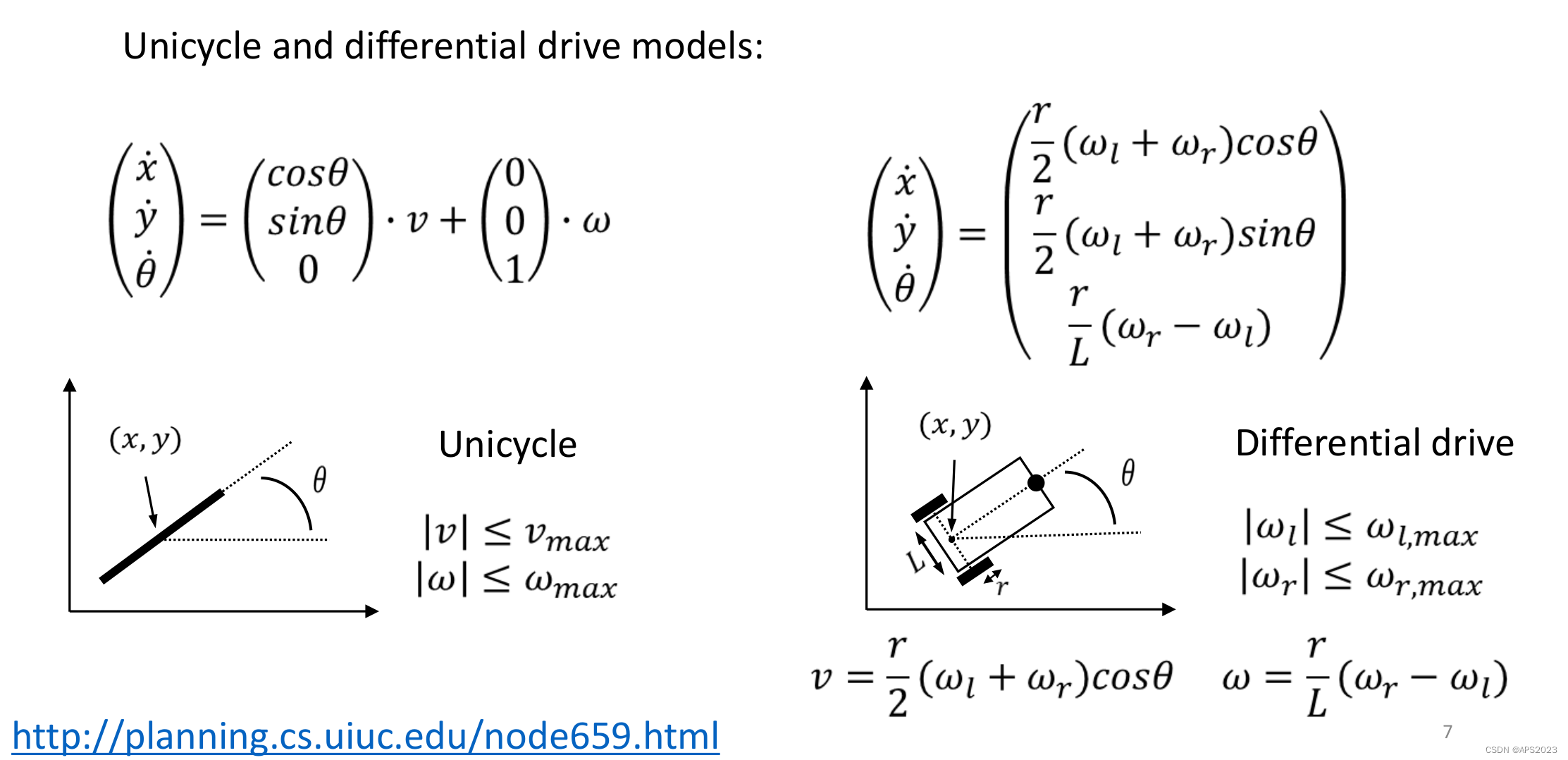
        这是一些经典的运动模型：

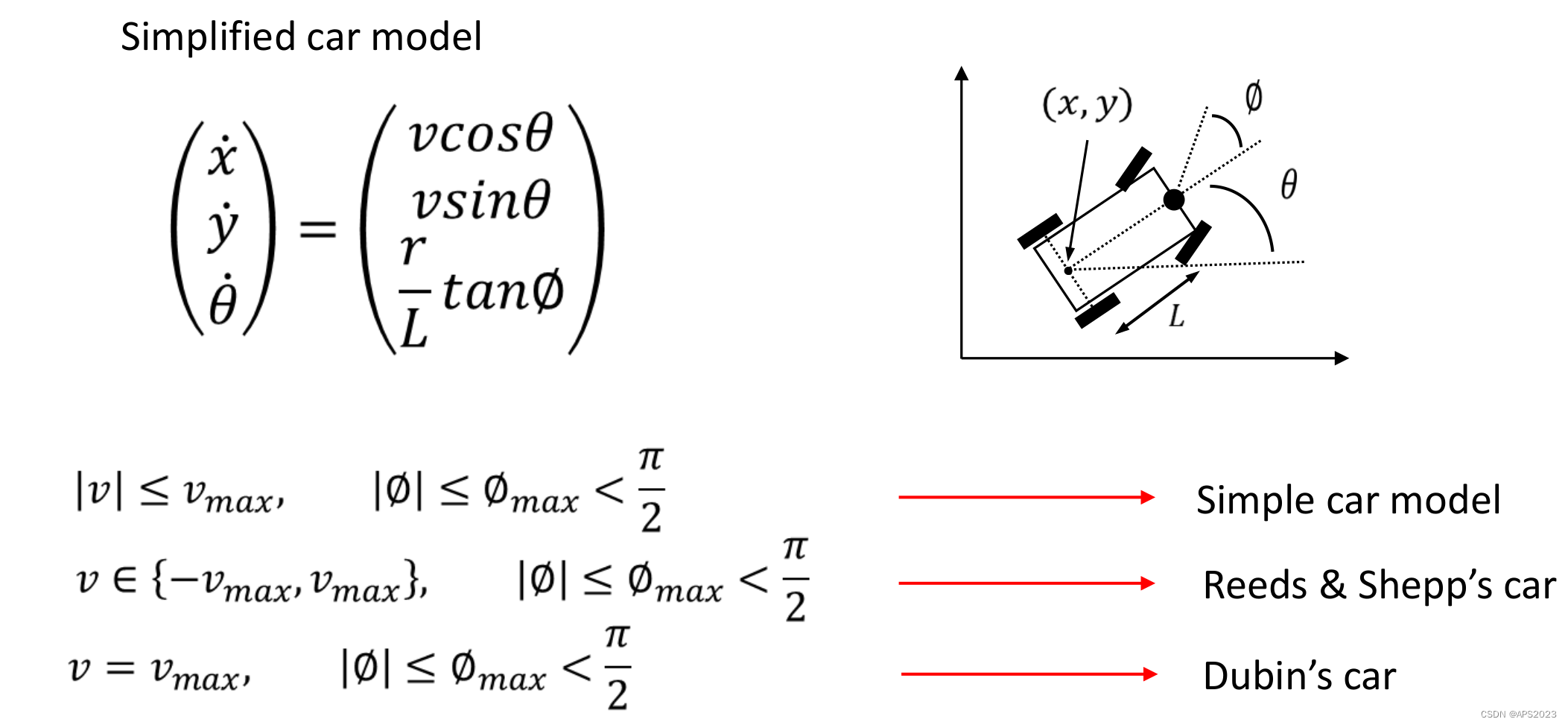
http://planning.cs.uiuc.edu/node659.htmlhttp://planning.cs.uiuc.edu/node659.html        下面是简化的小车的模型：

小车模型http://planning.cs.uiuc.edu/node658.html

2 State Lattice Planning

        We have many weapons to attack graph search.
        Assume the robot a mass point is not satisfactory any more.
        We now require a graph with feasible motion connections.

        We manually create (build) a graph with all edges executable by the robot.

        This is the basic motivation for all kinodyanmic planning.State lattice planning is the most straight-forward one.

        我们其实在第二章中已经完成了对机器人控制空间的离散：

        我们在第三章中的PRM，我们对机器人的状态空间离散化了：

        对于真正的机器人动力系统，我们要建立一个描述机器人运动的微分方程： $\dot{s} = f(s,u)$ ，s为机器人的状态（坐标，高阶导数速度加速度等），u是输入。

        我们需要知道机器人的初始状态以及描述机器人变化的微分方程 $\dot{s} = f(s,u)$

        如果我们选择不同的系统输入u，保持一段时间T，系统有不同的表现：（无导向性）

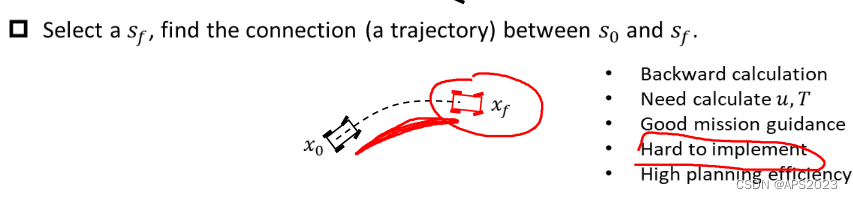
         在状态空间采样，选择一个终点的状态，从解出u，T：（有导向性、有贪心性质）

         我们看一下在控制空间采样的实例：

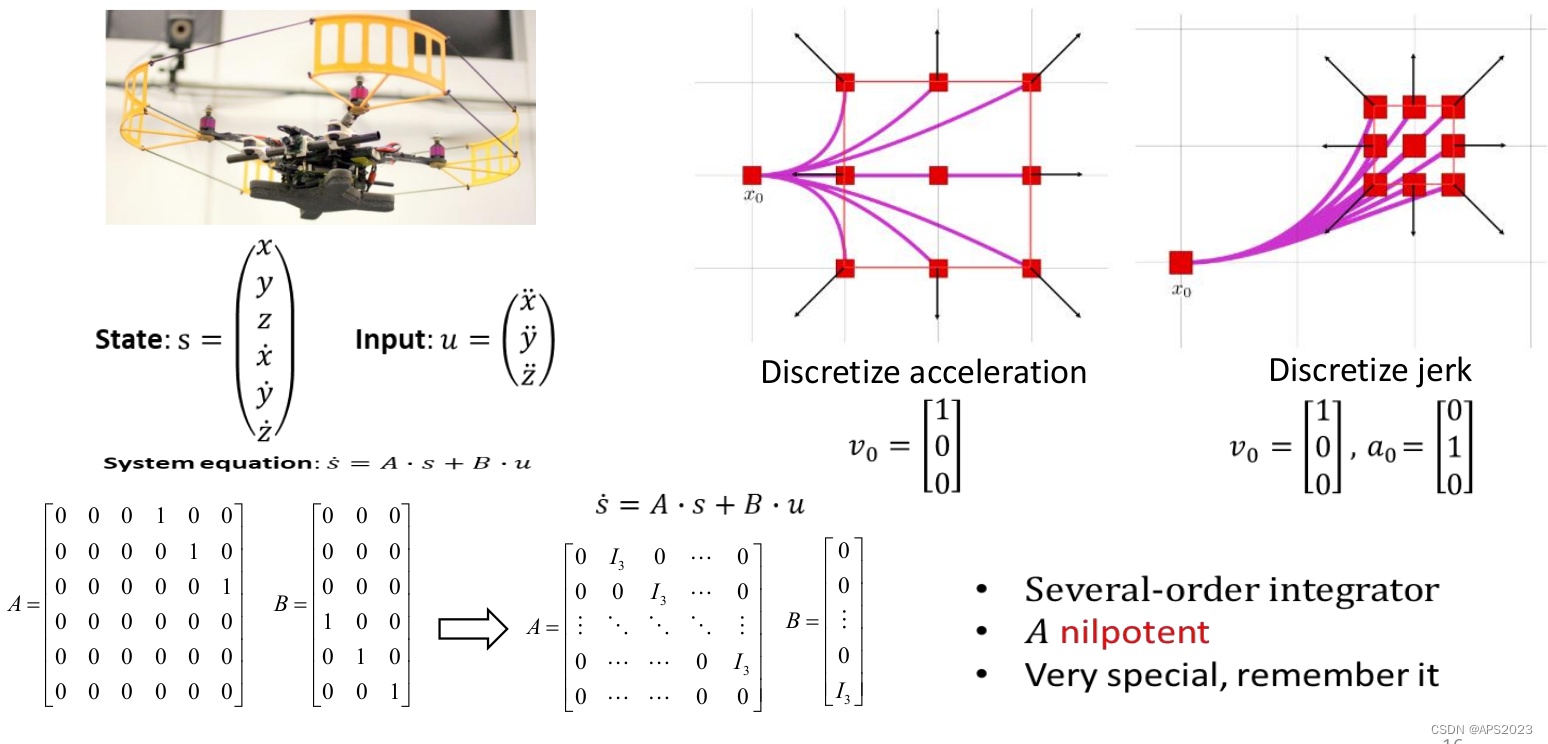
        输入的是u加速度作为控制的输入，状态量s为位置以及速度，系统的方程为线性方程：

        我们模型是加速度作为输入，系统的位置在，初速度为，我选取八个不同的状态给定不同的加速度给系统做一个前向的驱动，我们根据给定的位置、初速度为，在T=1.0时在什么位置。（就是系统在不同的初始状态下达到了某个状态）。

        高阶也是一样，不过初始的状态就是速度和加速度了。

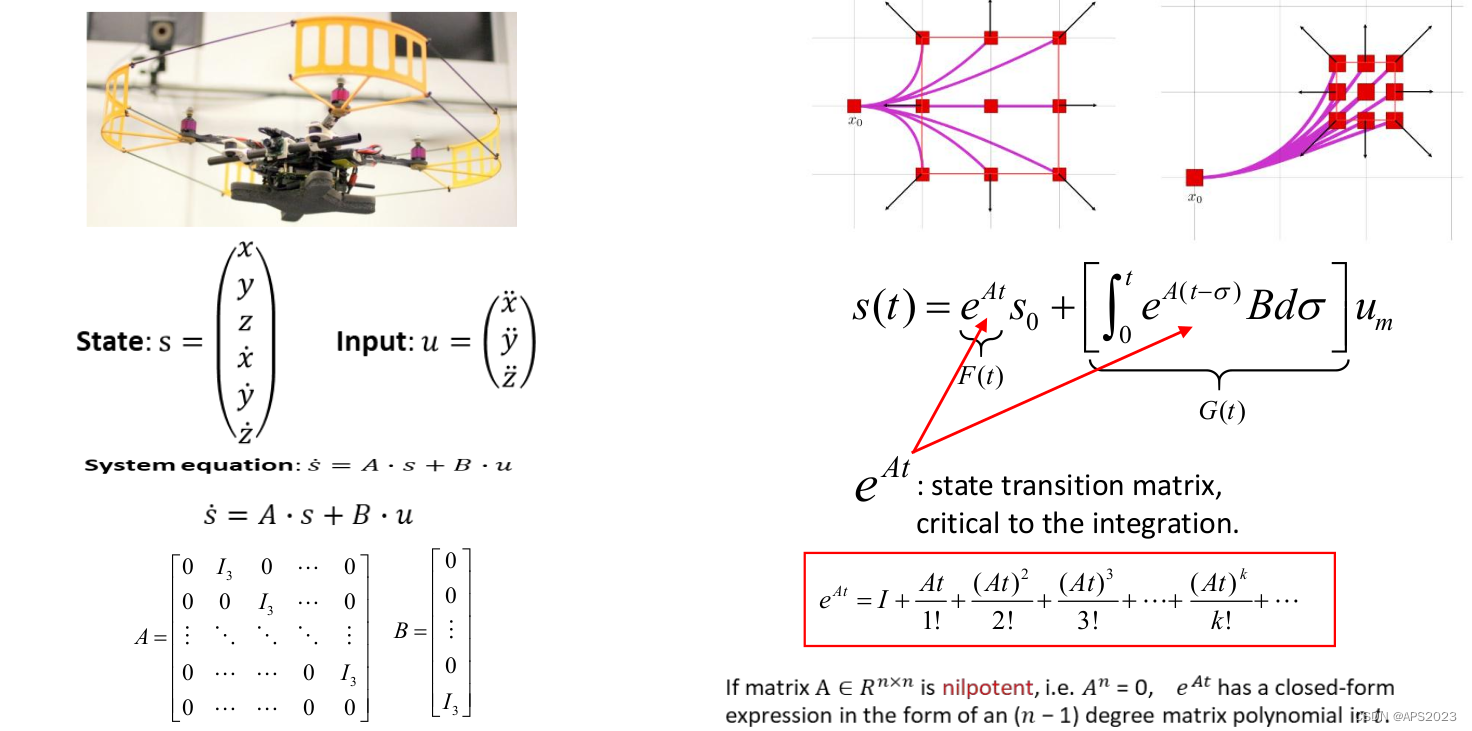
        那我怎么还原中间的运动呢？状态转移方程！！

        为随时间变化的函数，它和初始状态 $s_{0}$ 和整个运动过程选取的控制量（常数）关系。我们想知道 $t=\tau$ 时刻时状态到底是什么？

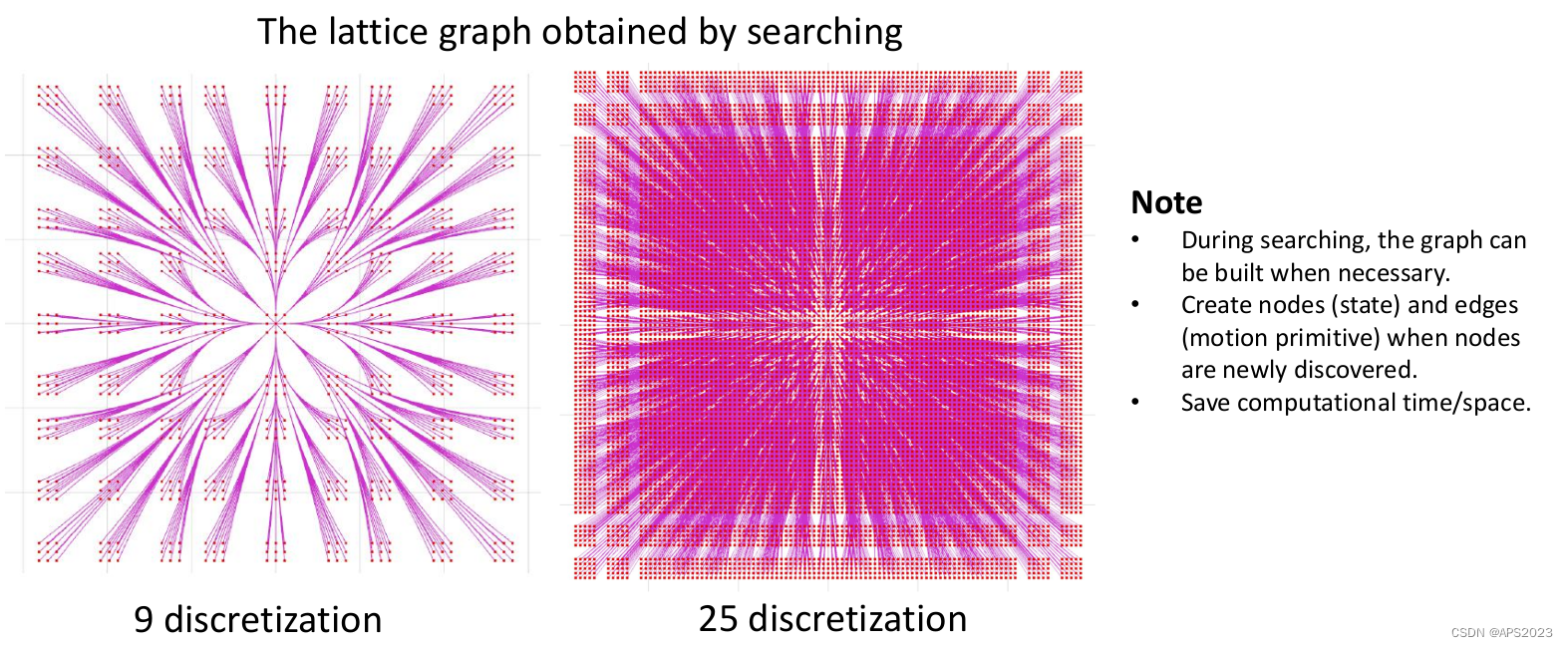
        那什么是State Lattice呢？

        这个图就是一个Lattice Gragh，其实就是给定一个初始的状态（初始状态：位置、速度），给定不同的控制高维输入（input）（加速度）让系统到达每个位置。然后我们在下一个地方依次做这些事情，就成了这个图。左图是九份离散化的图，右图是二十五份离散化的图。

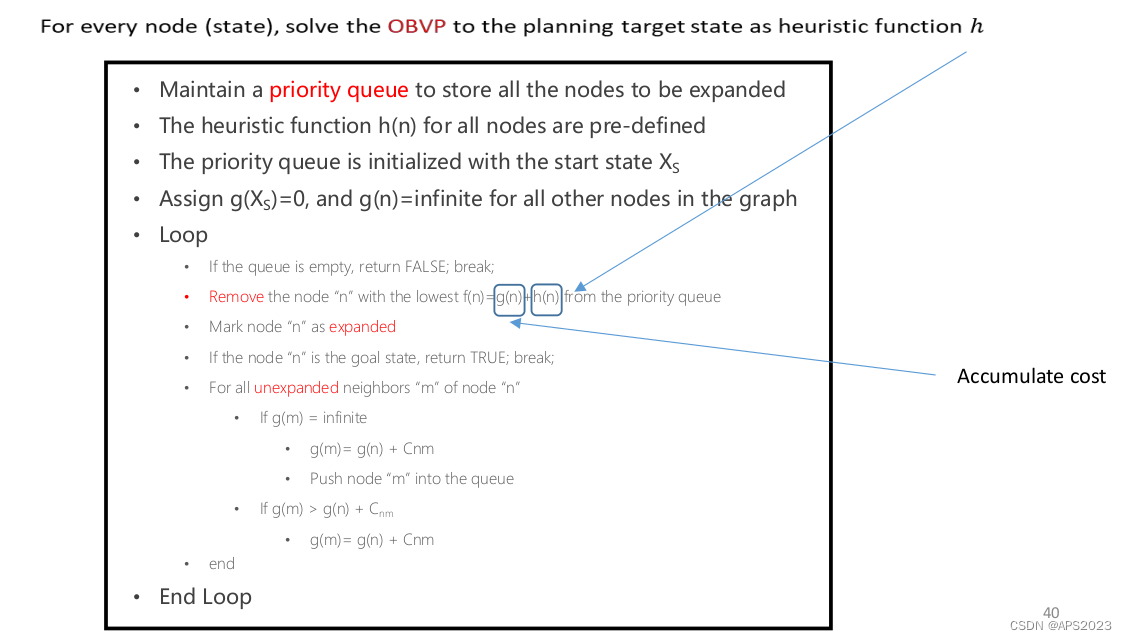
        思考？我们在search-base planing的时候，是不是一定要先给定初始状态，把所有的驱动信息都计算出来（把所有的graph建完之后），肯定不是！如果我们有一个非常好的启发式函数的话，其实可以非常有目的性的导向。（节省计算、存储成本）。

        如果我们是小车模型呢？

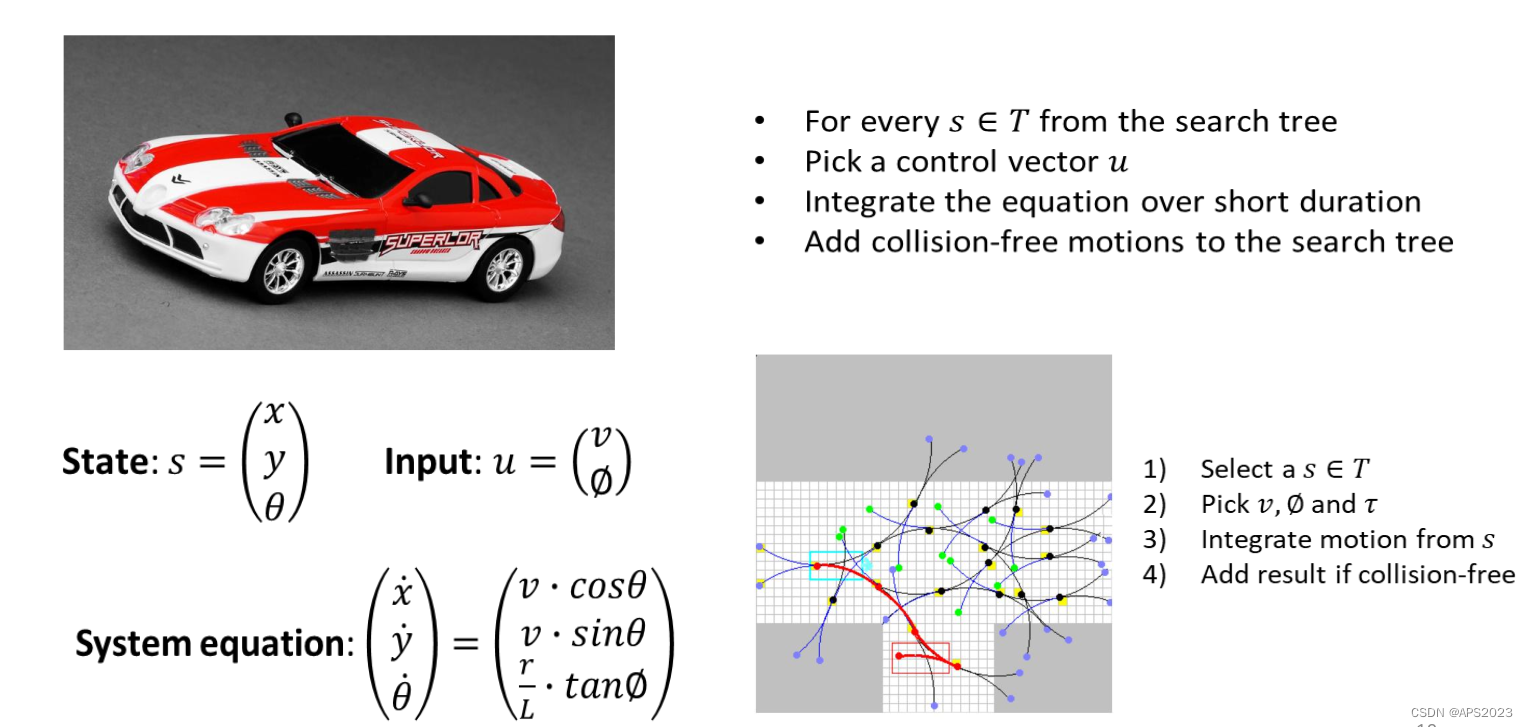
        我们用它的位置和朝向 $\theta$ 作为状态量来描述小汽车的模型，它的控制输入是油门和打方向盘的角度，如果我们想离散化控制输入得到一个搜索树怎么做呢？

        假设我们已经有一个搜索树了如右图，从搜索树找到一个节点，选择一个控制输入，固定一个时间 $\tau$ ，状态向前积分，如果边有障碍物则不可以，如果没有障碍物加入边。

        我们看一下在状态空间离散化的实例：

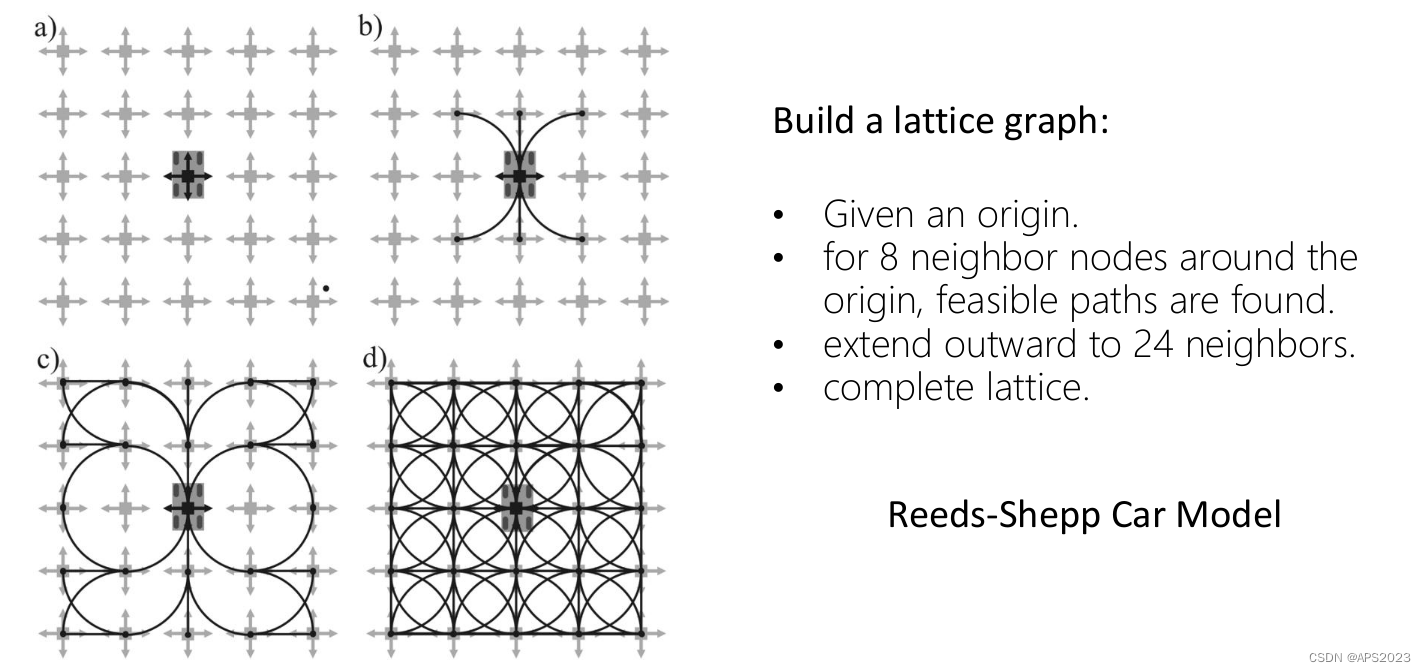
        先举一个例子，如果我们不考虑小汽车的模型，各个地方都可以运动，那么天然就是一张栅格地图，均匀的把地图进行切分：

        如果我们考虑汽车模型，也就是图b汽车不能左右侧滑的，只能6种运动方式，我们把这六种状态提取出来进行反演，看看这六条边如何到达的。

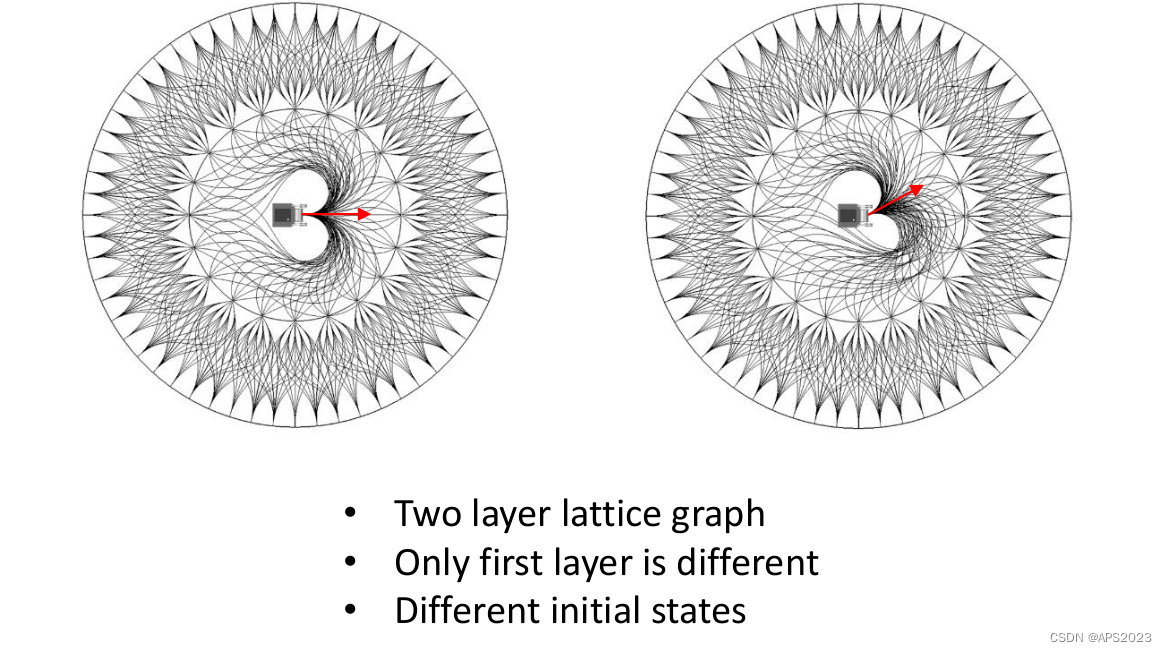
        如图是两层的lattice graph。

        比较一下：

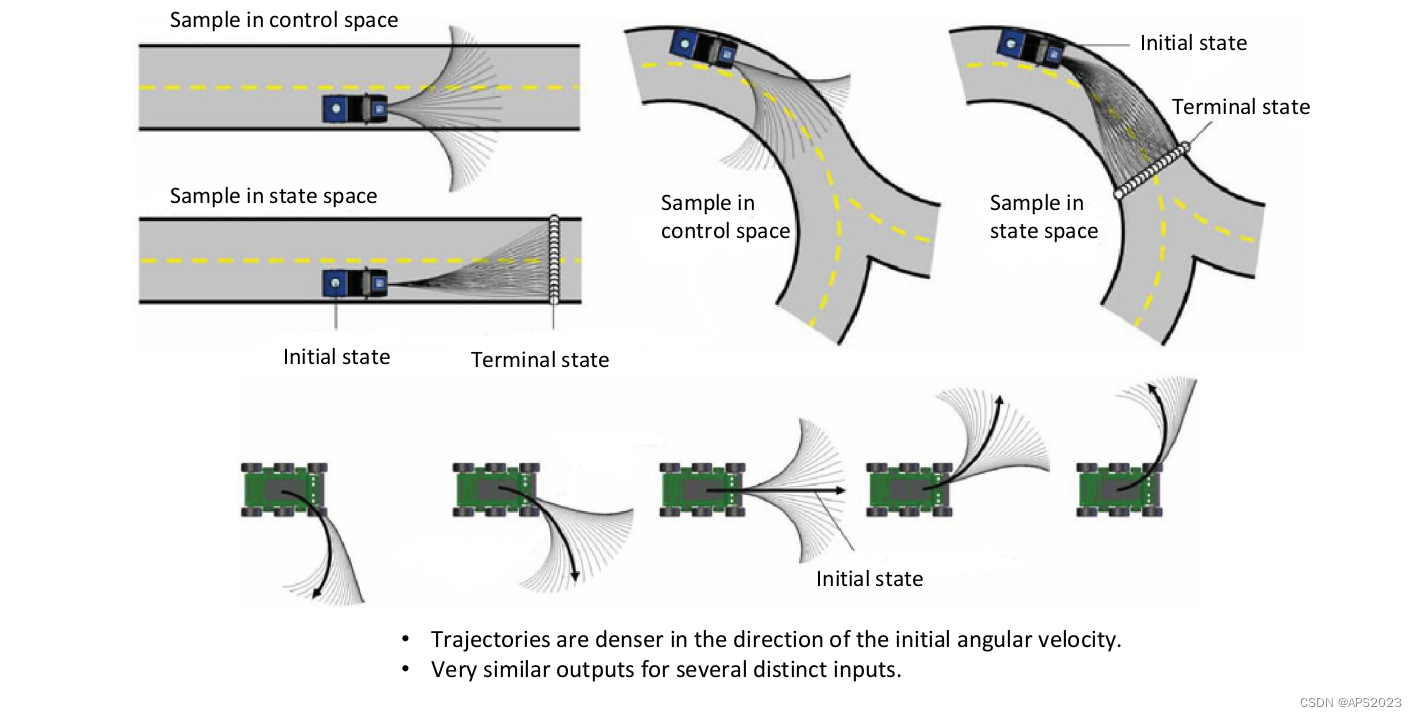
        1.控制空间采样没有目的性，状态空间采样（马路离散化很多份）可以保证目的性。

        2.离散化控制空间自由度很低（我们固定输入u在一段时间内只是匀速、匀加速....）会很大的受初始状态的影响。比如我们机器人前方有障碍物，如果我们离散的不均匀这次采样可能都撞车...

3 Boundary Value Problem

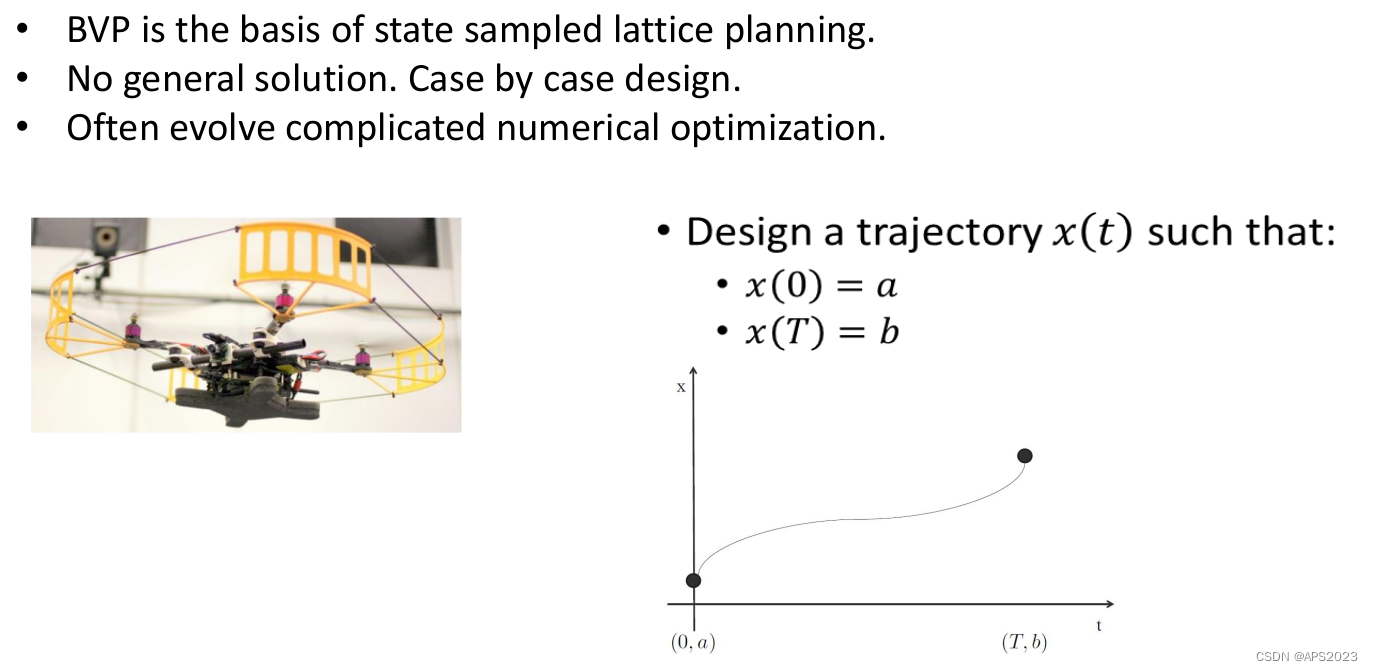
        我们来看最简单的Boundary Value Problem。

        假设一个一维的无人机系统，只考虑起点、终点的状态。

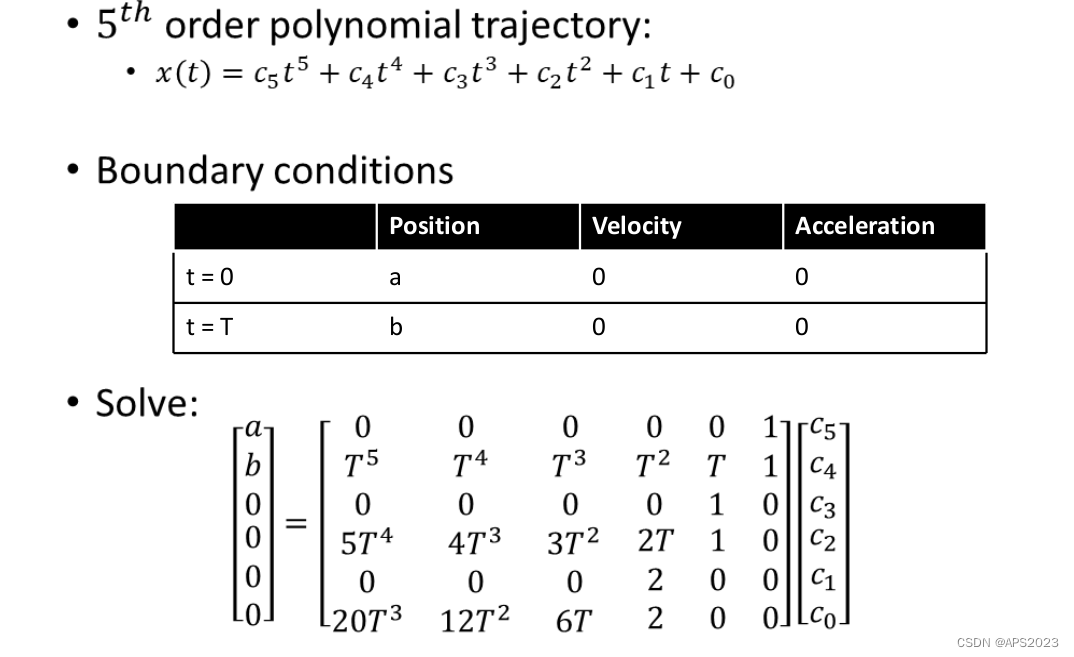
        一个简单的做法是将x的运动轨迹用多项式参数化：

        这个其实就是把时刻带入，，求导， ${x}'(t=0) = 5c_5t^4 + 4c_4t^3+3c_3t^2+2c_2t+c_1 = 0 = c_1$ ，同样在T点，求多阶导数也是一样，我们可以得到很多解，但是如何最好解呢？

        我们的问题：
        我希望我们无人机系统从一个状态到另一个状态，无人机系统在这段时间的jerk积分是最小的？！从OBVP解决（Optimal Boundary Value Problem (OBVP)）

        K表示在某个轴（我们简化问题，在某个轴独立运行），系统的状态量包含三个量：，选取的输入为加速度的导数。那么系统的模型 $\dot{s_k}$ 为求导，就不存在了。因此 $\dot{s_k} = f_s(s_k,u_k) = (v_k,a_k,j_k)$ 。

        如何解决：极小值原理

        我们需要定义问题的三个协态costate， $\lambda = (\lambda_1, \lambda_2 ,\lambda_3 )$ ，System model有多少个变量，就有多少个costate，我们接着定义Hamiltonian function，它的获得方法如下：

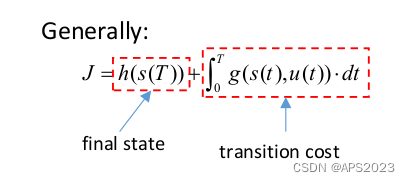
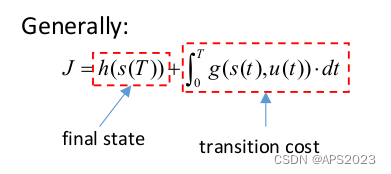
        通常来说，最优控制的问题目标函数由两项定义：

        终末状态的惩罚项（T时刻的状态有没有到一个状态）、系统在运行过程中的能量的损耗。

        首先要写出汉末雅顿方程把协态应用进去：

        它是关于系统的变量s，输入u以及协变量 $\lambda$ 的方程。我们要求解的是最优的以及最优的控制输入 $u^{*}$ 。它用下列的微分方程来解决：

        太抽象了....

        这里的就是

         $\lambda$ 的导数：H对 $\lambda _k$ 的求导（p、v、a）

        解微分方程，其实是一组解：

        我们先求，使得汉末雅顿方程最小的解，我们把 $\lambda$ 、带入：

        因为已经是最好的了，因此也出来了，我们只需要考虑H的第一项和第四项：其实就是求 $\frac{1}{T}j^2 + \lambda _3j$ 的极值。那么就对求导让其等于0即 $\frac{2}{T}j + \lambda _3=0$ 。j的最优解我们可以求出。带入可以求出：

        那么怎么求呢？直接积分就可以了。

        我们就解出来啦～，记得把初始条件T=0时刻的边界条件代进去。

        现在还有 $\alpha ,\beta ,\gamma$ 没确定，我们用末尾边界条件来确定。

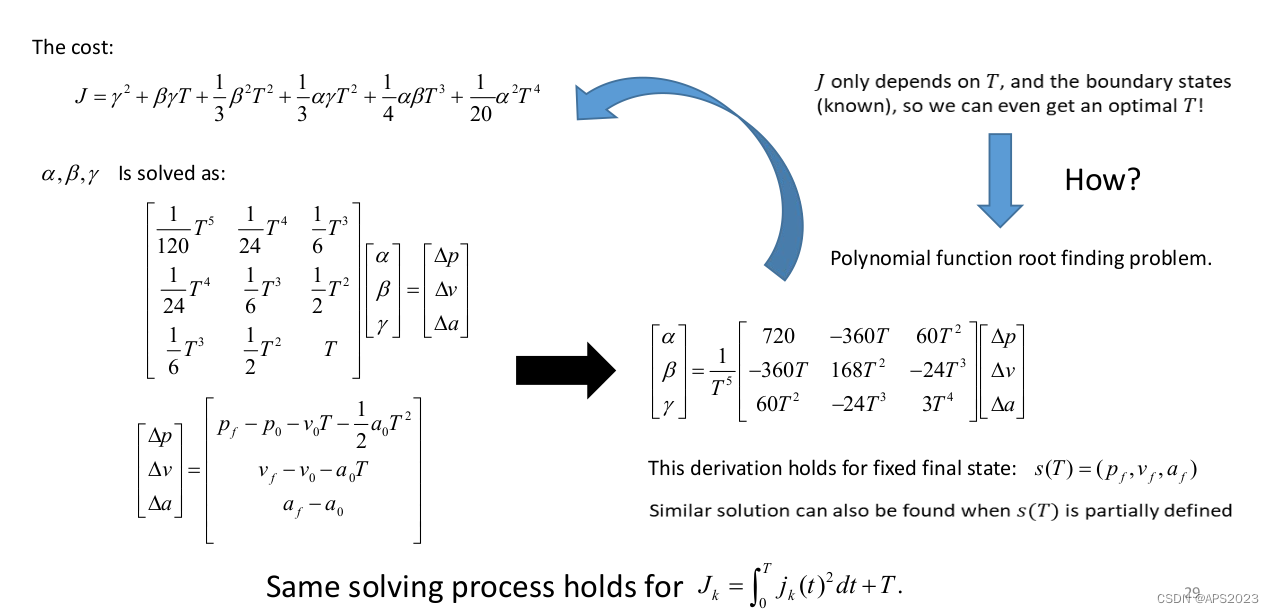
        J只和T有关！

        因此我们做的就是给定一个初始的state，给定一个末尾的state怎么求出一个最优解。

        启发式函数：假设不存在障碍物、假设不考虑动力学。

        具体的形式如下：

4 混合A算法 Hybrid A

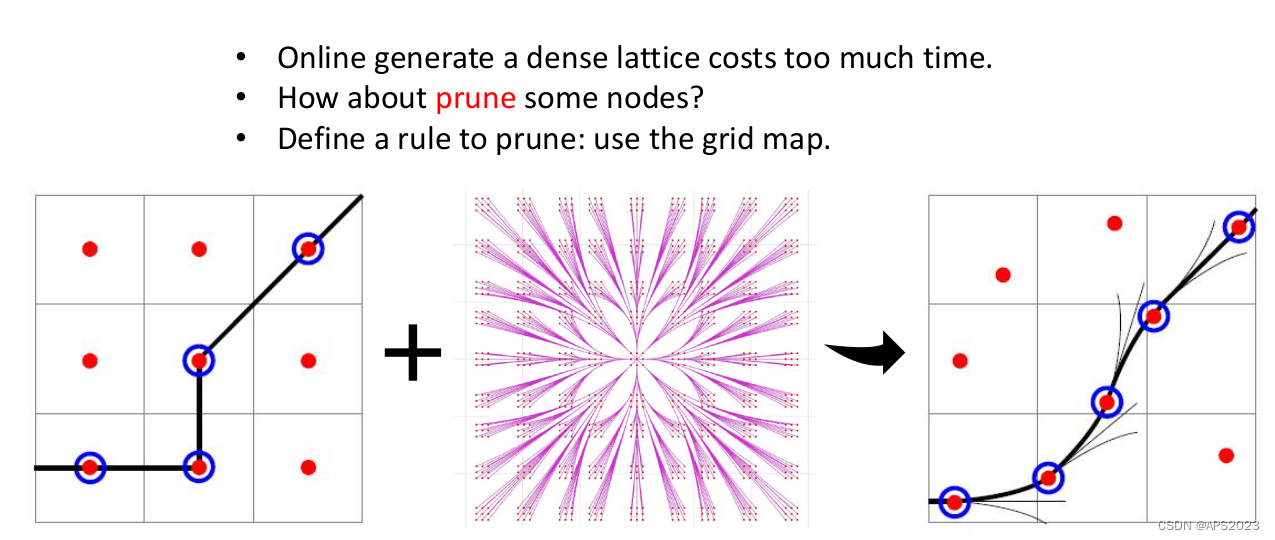
        流程如何呢？我们前面说过了在栅格地图上进行A*算法就是在栅格地图找一条path，Lattice Planning是自己构建一个搜索图或者搜索树（这里我们要给定一个机器人模型将控制空间离散化），比如说我们取控制空间为 $u\epsilon [-u_{max},+u_{max}]$ ，在可行控制空间中我们把控制空间做多等分，用每一个控制空间把系统做前向的推移。会得到一个非常稠密的Lattice Planning。（能不能结合栅格地图进行剪枝使控制空间更鲁棒性，不会出现前面的问题）。

        其实就是在搜索过程中我选取不同的control input驱动系统不同向前积分，积分出来的系统的机器人的state在栅格地图的每一个节点只记录一个机器人可行的state。如图三。

        看一下代码：

        对比普通A*：

        启发式函数：选择动力学相关的启发式函数

        扩展节点：A*找左右上下邻居，JPS找左右斜对角跳点的邻居，Hybrid A*寻找控制输入的驱动下去找系统的state邻接的state的过程。

        记录state、g值更新（更好路径的赋予）也不一样。.

        如何设计更好的启发式函数呢？

        1.二维欧式距离

        2.不考虑障碍物考虑动力学的启发式函数

        3.不考虑障碍物考虑动力学的启发式函数可能在碰见死胡同的时候出现问题

        4.不考虑障碍物考虑动力学 + 考虑障碍物不考虑车辆动力学最短路径（MAX）

        Analytic Expansions（trick）：在树的生长过程中（搜索树）以一定的概率去解和终点为解的路径。

5 Kinodynamic RRT*

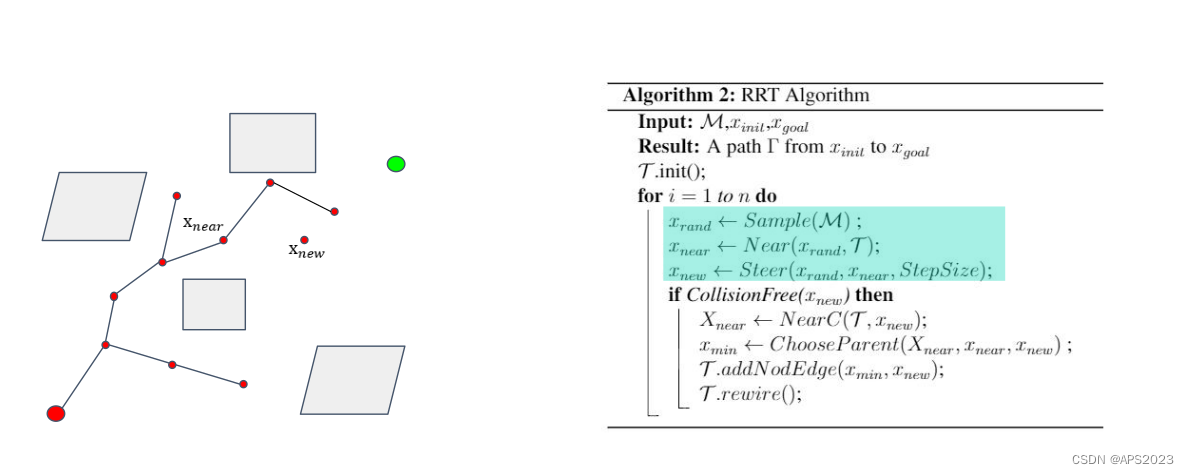
        回顾一下RRT*的流程：

        Kinodynamic RRT* VS RRT*：

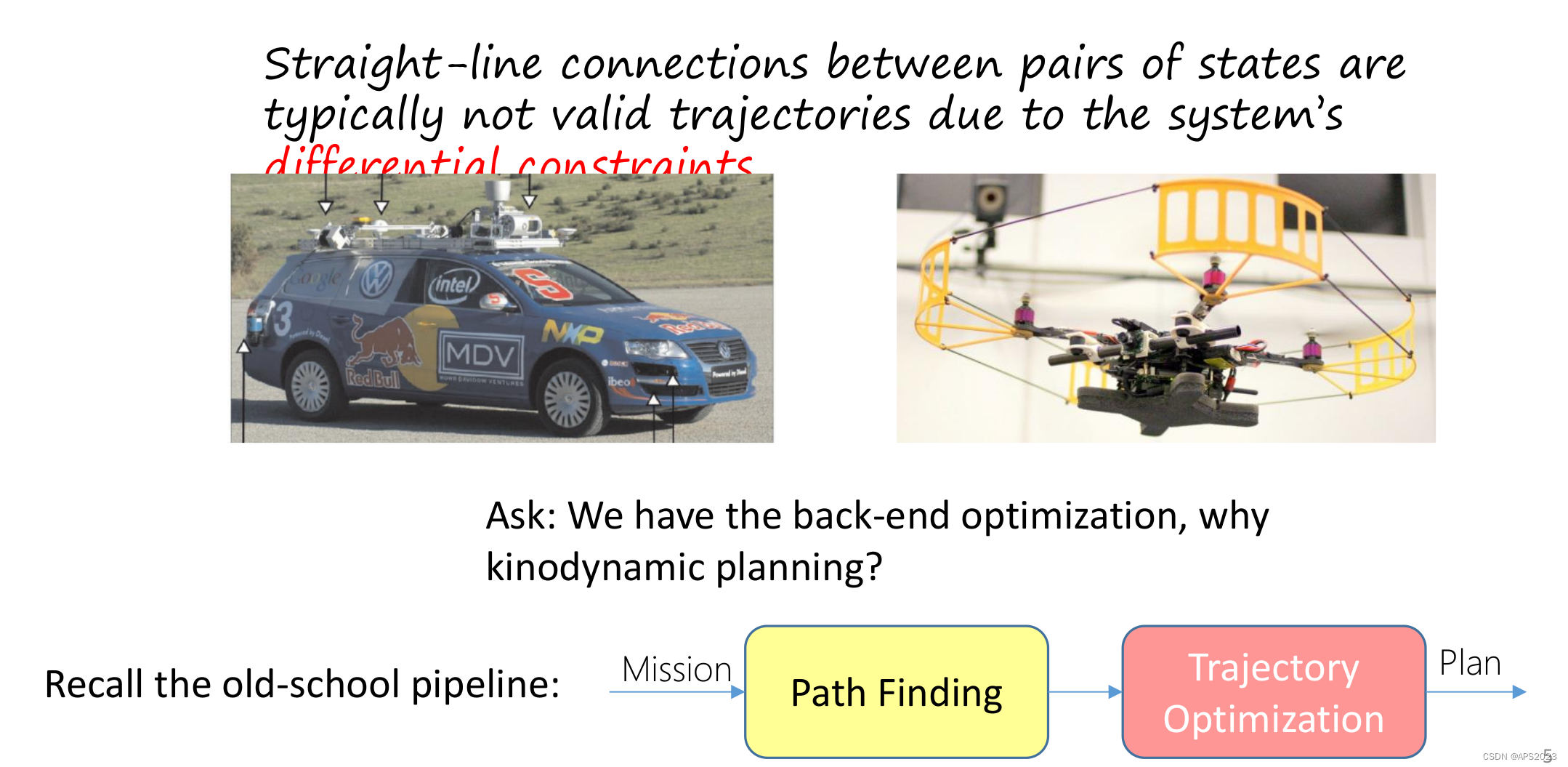
        不同点：采样了新的节点以后进行局部连接，在RRT*中不考虑机器人的运动直接连接直线就可以，但现在机器人用微分方程去描述了，就要解两点边界值问题。

        我们从头看：

        如何采样：现在的状态空间已经扩展了，比如说是个线性系统。我们就要在它全部的运动空间采样。

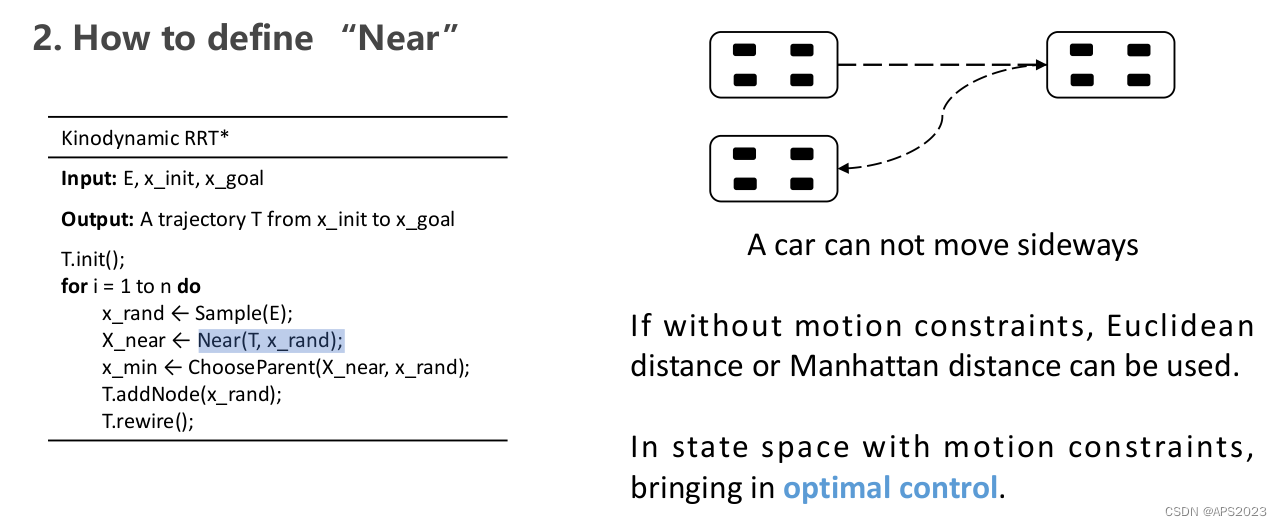
        如何定义邻近节点：

        用optimal control的知识把新采样的state和邻近节点的state进行OBVP连接。

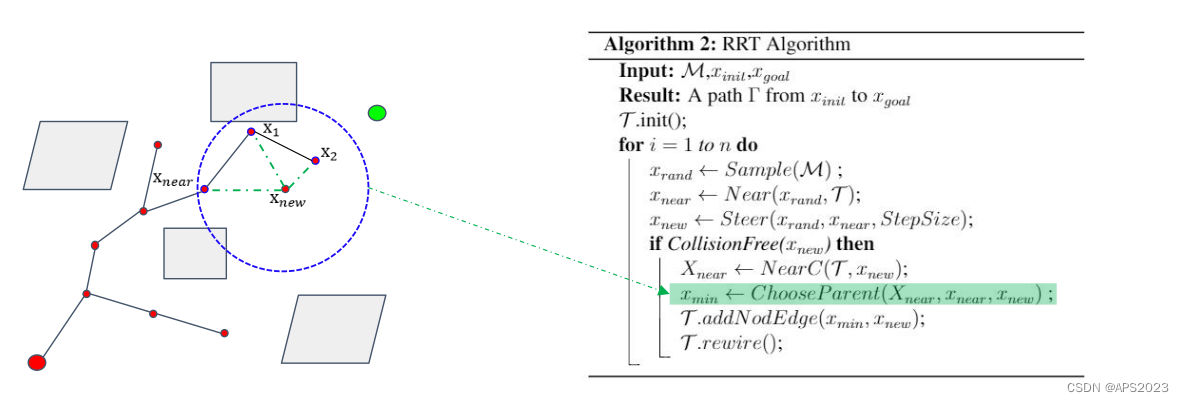
        3.如何选择父亲节点：

        如何构造球呢？用控制方法!