傅里叶变换

一维傅里叶变换：

https://zhuanlan.zhihu.com/p/19763358

离散的频谱图像,其中时域图像y=f(t)，横轴是t,纵轴是y;  其对应的频域包括：振幅（体现在频域图像中：横坐标是频率，纵坐标是振幅），相位（体现在相位谱中：横坐标是频率，纵坐标是相位值）和频率。

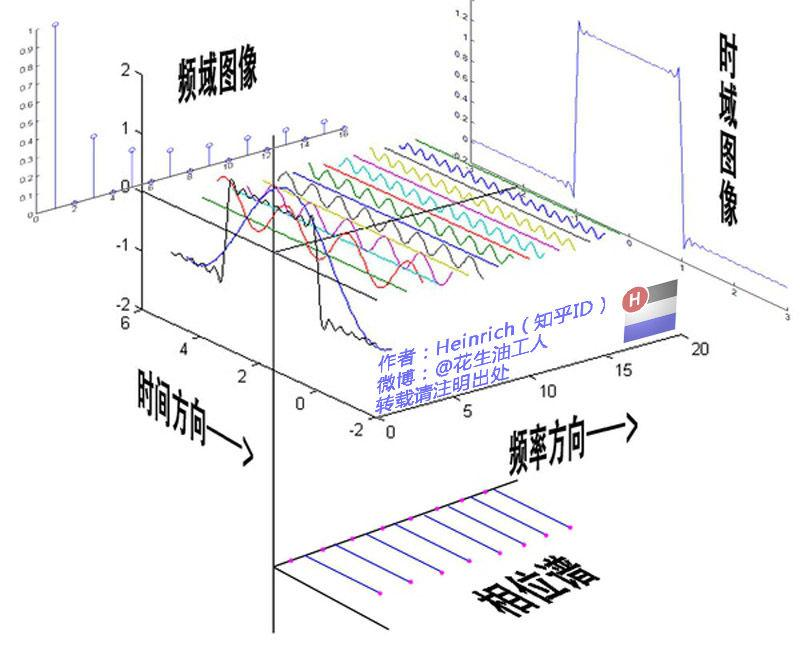
傅里叶变换：

任意信号都可以由一组正弦曲线组合而成；对于连续周期信号，其对应的频谱是离散的，组合方式为（∑）；对于非周期信号，可以认为其周期是无限大，其对应的频谱是连续的，组合方式为∫ 。

连续的傅里叶级数：

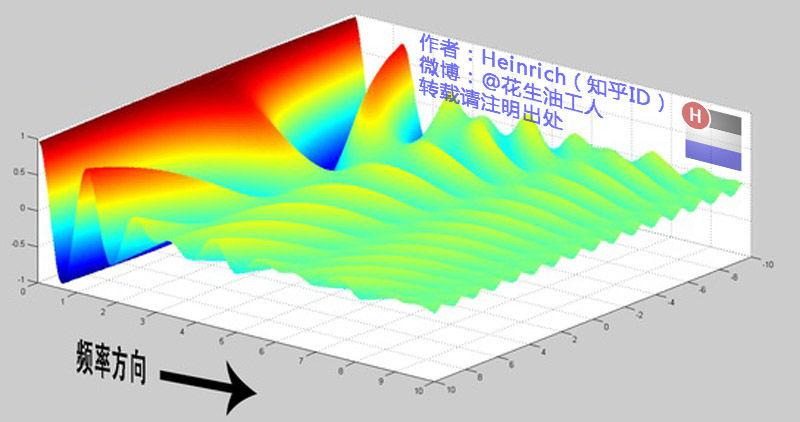
一维傅里叶变换公式：

t是时间，T是频率

傅里叶变换的理解：

傅里叶反变换的直观理解（频域到时域）：

 

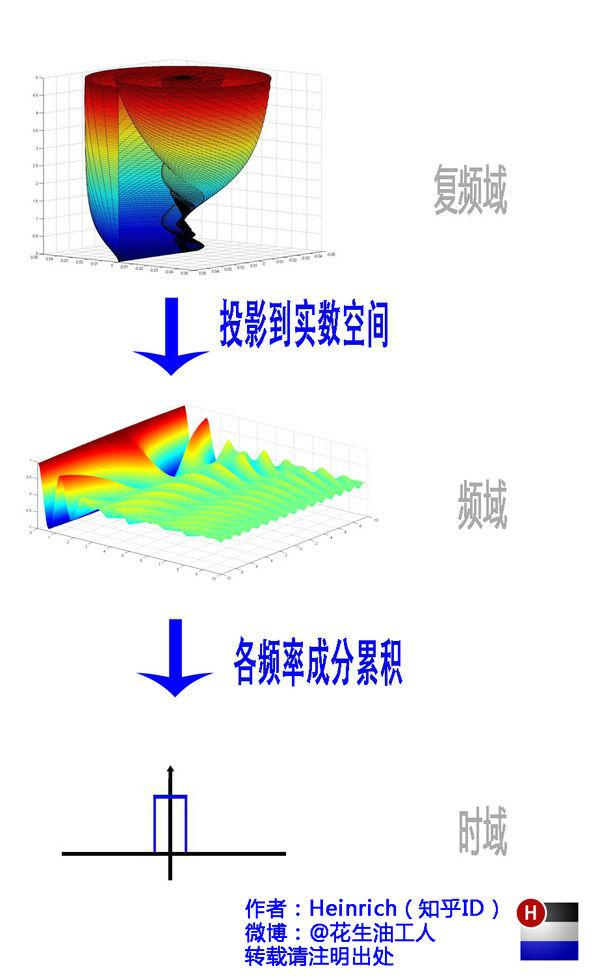
一维傅里叶变换的作用：

（1）信息传输中的滤波：低频信息变化缓慢，而高频信息变化迅速；针对信息传输中噪声的频率成分，进行滤波去除噪声

 

二维傅里叶变换：

关键：理解频率图像的含义

参考https://zhuanlan.zhihu.com/p/99605178?utm_source=qq

https://www.zhihu.com/question/22611929

（1）一维傅里叶变换是正弦信号的叠加，而二维傅里叶变换是正弦平面波的叠加。各个不同频率的正弦平面波，叠加后构成不同的灰度值。

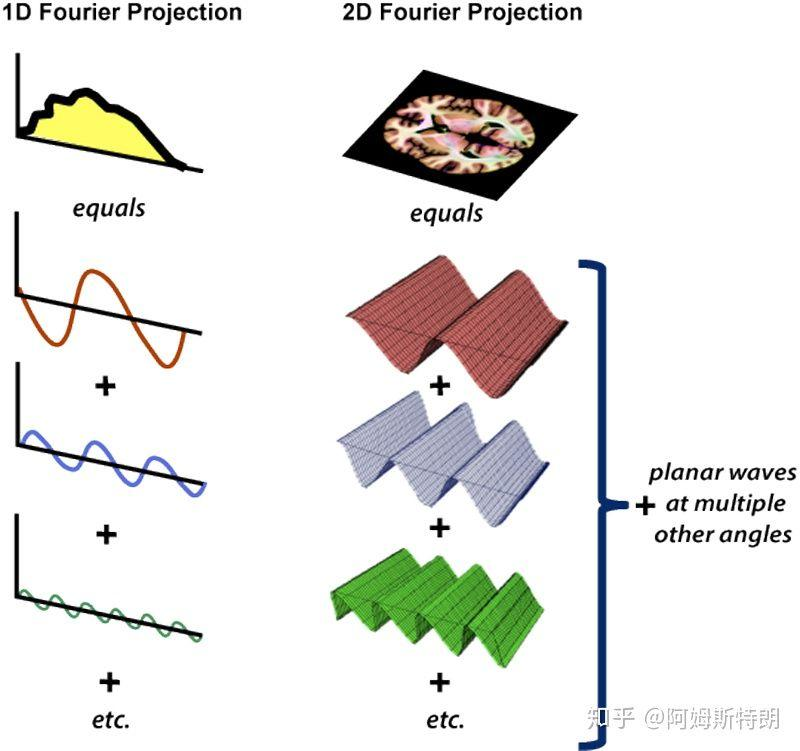
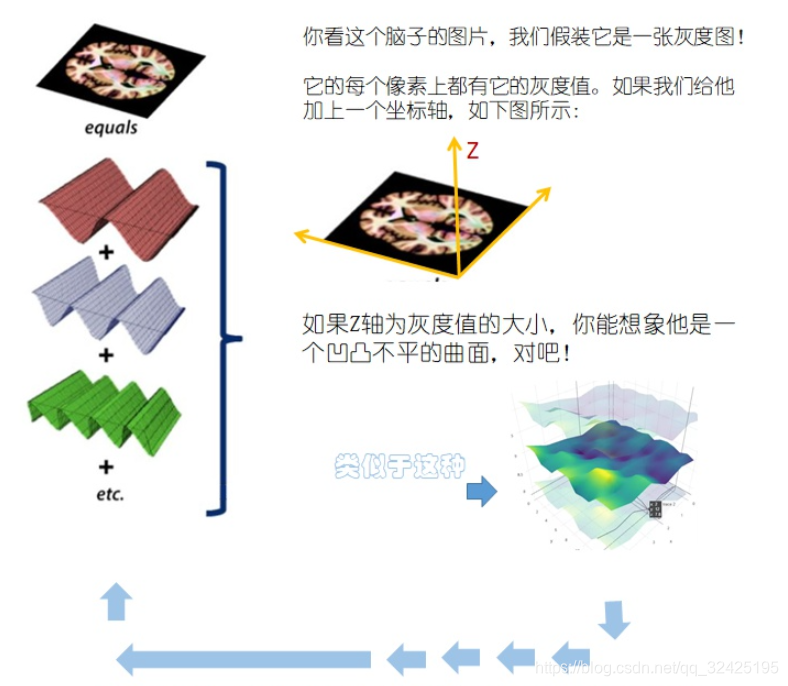
（2）二维傅里叶变换公式的含义：

公式中，x,y是连续空间变量，u,v是连续频率变量。二维傅里叶变换将二维信号f(x,y)分解为若干个复平面波。若干个复平面波可以用二维频率域K-SPACE表示。

若干个复平面波，每个波包括：频率w,幅度A,相位，方向

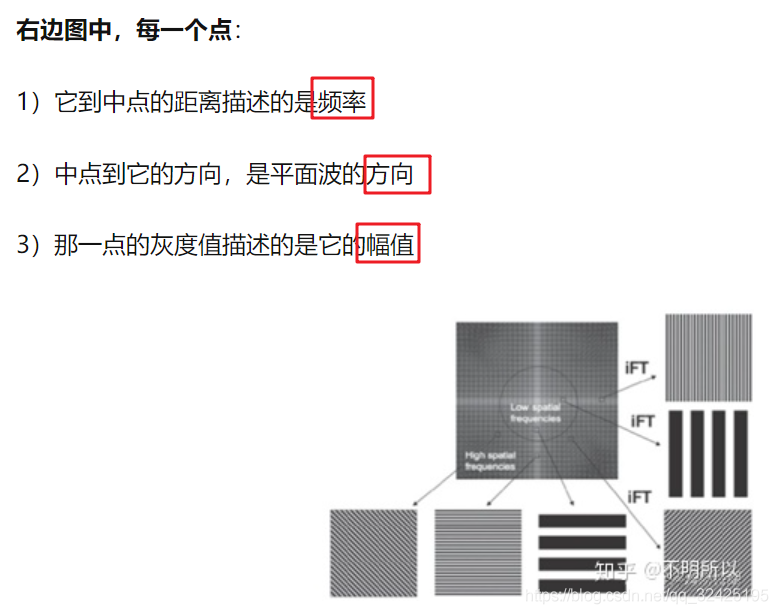
二维傅里叶变换的作用：

频域滤波来去除指定频率的数据；中心低频贡献了图像的主体，周围高频提供图像的细节和边缘