【数据结构--栈的顺序存储结构】
栈的顺序存储结构
栈的定义
栈(stack)是限定仅在表尾进行插入和删除的线性表
允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈。栈又称为先进后出的线性表,简称LIFO结构。
栈的插入操作,叫做进栈,也称为压栈、入栈,如下图所示。
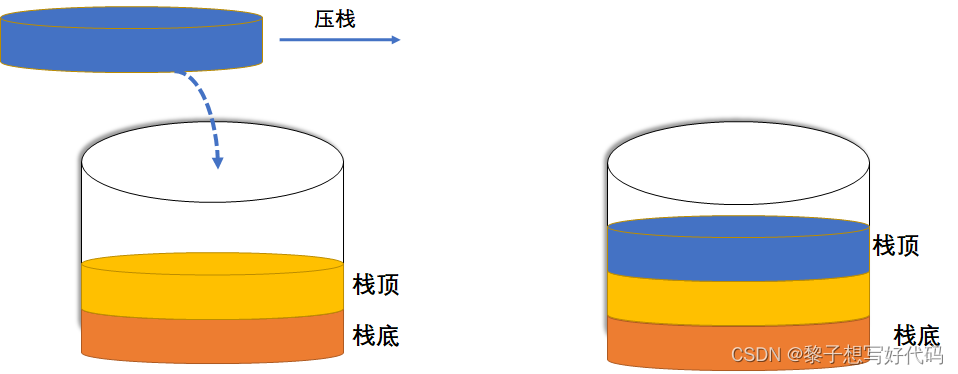
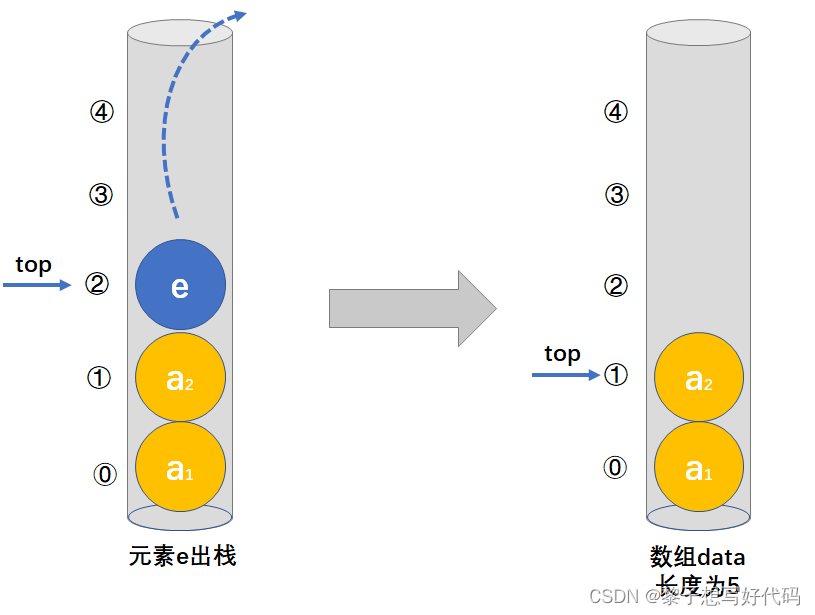
栈的删除操作,叫做出栈,也称为弹栈,如下图所示。
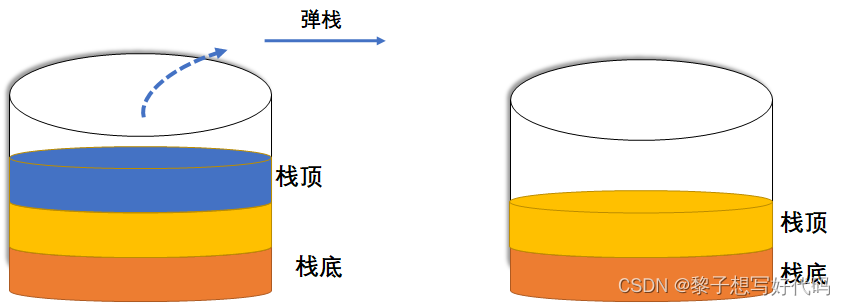
栈的结构定义:
typedef struct CharStack
{
int top; /* 用于栈顶指针 */
int data[MAXSIZE];
} *CharStackPtr,CharStack;
栈的初始化
栈的初始化即为顺序栈动态分配一个预定义大小的数组空间
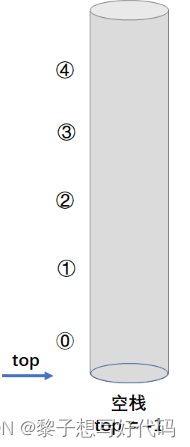
代码如下:
//初始化栈
CharStackPtr CharStackInit()
{
CharStackPtr resultPtr = (CharStackPtr)malloc(sizeof(CharStack));
resultPtr->top = -1;
return resultPtr;
}
压栈操作
压栈即为在栈顶插入一个新元素
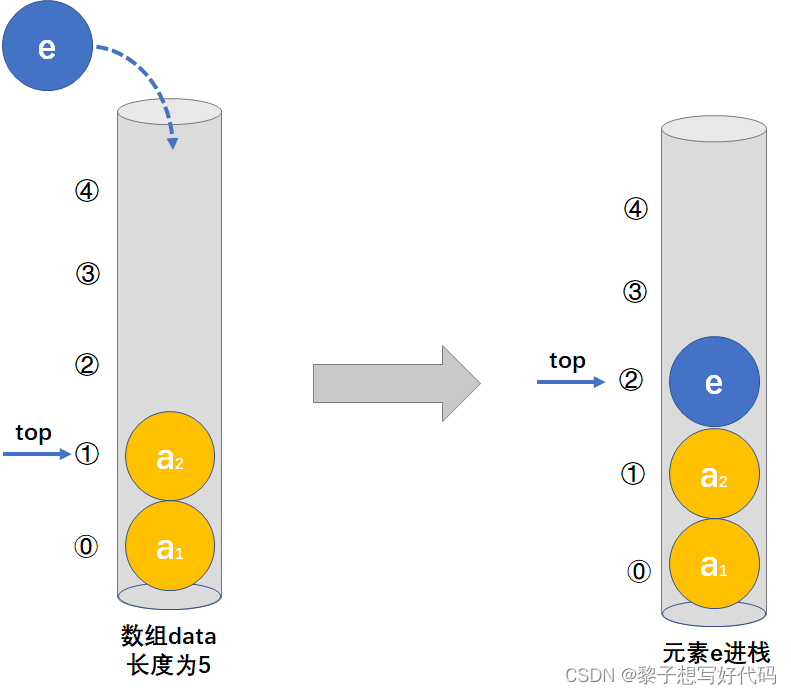
代码如下:
//压栈
void push(CharStackPtr tempStackPtr, char tempValue)
{
if(tempStackPtr->top >= MAXSIZE - 1)
{
printf("无法压入元素%c:堆栈已满!\n",tempValue);
return ;
}
tempStackPtr->top ++;
tempStackPtr->data[tempStackPtr->top] = tempValue;
}
弹栈操作
弹栈即为将栈顶元素删除
代码如下:
//弹栈
char pop(CharStackPtr tempStackPtr)
{
if (tempStackPtr->top == -1)
{
printf("不能弹出元素:堆栈为空!\n");
return NULL;
}
tempStackPtr->top --;
return tempStackPtr->data[tempStackPtr->top+1];
}
返回栈顶元素
//返回栈顶元素
char GetTop(CharStackPtr tempStackPtr)
{
if(tempStackPtr->top == -1)
{
printf("栈为空:无法返回!\n");
return NULL;
}
return tempStackPtr->data[tempStackPtr->top];
}
返回栈的长度
//返回栈的长度
int StackLength(CharStackPtr tempStackPtr)
{
return tempStackPtr->top + 1;
}
将栈清空
//将栈清空
void ClearStack(CharStackPtr tempStackPtr)
{
tempStackPtr->top = -1;
return ;
}
完整代码
#include <stdio.h>
#include <malloc.h>
#define MAXSIZE 10
typedef struct CharStack
{
int top; /* 用于栈顶指针 */
int data[MAXSIZE];
} *CharStackPtr,CharStack;
//输出栈
void outPutStack(CharStackPtr tempStack)
{
for(int i = 0; i <= tempStack->top; ++i)
{
printf("%c ",tempStack->data[i]);
}
printf("\n");
}
//初始化栈
CharStackPtr CharStackInit()
{
CharStackPtr resultPtr = (CharStackPtr)malloc(sizeof(CharStack));
resultPtr->top = -1;
return resultPtr;
}
//压栈
void push(CharStackPtr tempStackPtr, char tempValue)
{
if(tempStackPtr->top >= MAXSIZE - 1)
{
printf("无法压入元素%c:堆栈已满!\n",tempValue);
return ;
}
tempStackPtr->top ++;
tempStackPtr->data[tempStackPtr->top] = tempValue;
}
//弹栈
char pop(CharStackPtr tempStackPtr)
{
if (tempStackPtr->top == -1)
{
printf("不能弹出元素:堆栈为空!\n");
return NULL;
}
tempStackPtr->top --;
return tempStackPtr->data[tempStackPtr->top+1];
}
//返回栈的长度
int StackLength(CharStackPtr tempStackPtr)
{
return tempStackPtr->top + 1;
}
//返回栈顶元素
char GetTop(CharStackPtr tempStackPtr)
{
if(tempStackPtr->top == -1)
{
printf("栈为空:无法返回!\n");
return NULL;
}
return tempStackPtr->data[tempStackPtr->top];
}
//将栈清空
void ClearStack(CharStackPtr tempStackPtr)
{
tempStackPtr->top = -1;
return ;
}
//测试
void ComprehensiveTest()
{
printf("--------初始化栈--------\n");
CharStackPtr tempStack = CharStackInit();
printf("--------初始化后的栈为--------\n");
outPutStack(tempStack);
printf("--------压栈--------\n");
for (char ch = 'a'; ch < 'm'; ++ ch)
{
printf("压入 %c.\n",ch);
push(tempStack,ch);
outPutStack(tempStack);
}
printf("--------返回栈的长度--------\n");
int stacklength = StackLength(tempStack);
printf("栈的长度是%d\n",stacklength);
printf("--------返回栈顶元素--------\n");
char topch = GetTop(tempStack);
printf("栈顶元素是%c\n",topch);
printf("--------弹栈--------\n");
for (int i = 0; i < 3; ++i)
{
char ch = pop(tempStack);
printf("弹出 %c\n",ch);
outPutStack(tempStack);
}
printf("--------清空栈--------\n");
ClearStack(tempStack);
outPutStack(tempStack);
}
int main()
{
ComprehensiveTest();
}
测试结果
--------初始化栈--------
--------初始化后的栈为--------
--------压栈--------
压入 a.
a
压入 b.
a b
压入 c.
a b c
压入 d.
a b c d
压入 e.
a b c d e
压入 f.
a b c d e f
压入 g.
a b c d e f g
压入 h.
a b c d e f g h
压入 i.
a b c d e f g h i
压入 j.
a b c d e f g h i j
压入 k.
无法压入元素k:堆栈已满!
a b c d e f g h i j
压入 l.
无法压入元素l:堆栈已满!
a b c d e f g h i j
--------返回栈的长度--------
栈的长度是10
--------返回栈顶元素--------
栈顶元素是j
--------弹栈--------
弹出 j
a b c d e f g h i
弹出 i
a b c d e f g h
弹出 h
a b c d e f g
--------清空栈--------
总结
-
栈本身就是一个线性表,栈的顺序存储结构其实也就是线性表顺序存储结构的简化
-
任何弹栈的元素后面弹栈的元素必须满足以下两点:
- 在原序列中相对位置比它小的,必须是逆序
- 在原序列中相对位置比它大的,顺序没有要求