图的深度优先和广度优先遍历

图的遍历

  图的遍历指从某一个顶点出发按照一定的线路对其余各个顶点进行访问，通常访问的顺序有深度优先和广度优先两个方向。数据结构中链型结构，如链表，顺序表等，还有树形结构，如二叉树等都属于图的一种退化，链形结构通常是顺序遍历直接使用for循环即可，树形结构的访问相对比较复杂，对于二叉树有先序遍历，中序遍历等，而其中的层次遍历就是广度优先遍历，与广泛意义的图不一样的是，树的遍历往往从根节点开始，依照数据存储习惯不用孩子父亲表示法则很难往回访问，所以一般不能从任意节点开始遍历，而图则可以从任意起点开始！

图的存储结构

  不同于链表和树，图的存储通常使用一个正方形的矩阵或者一个list容器。方形矩阵很好解释，矩阵坐标为(i,j)的元素就可以表示从第i个顶点到第j个顶点的权重，这样的表示方法同时也方便统计顶点的出度和入度，而用链表来存储的方式就是通常所说的邻接链表法，一个链表用于存放各个顶点然后链表的每个节点作为头可以横向链接当前节点往外出的节点。

一个例子

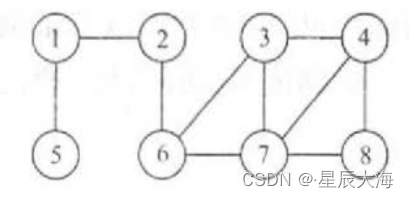
  上述例子来自王道书，是一个无向图。尝试从节点1开始分别使用深度优先遍历和广度优先遍历来访问各个节点。深度优先遍历就是所谓的“一条路走到黑”，从1开始往5的方向走很快就见底，这样便完成了一次深度优先遍历，检查各个节点是否都被访问过，显然2、6等节点均未被访问，则需要接着从1的另一个方向开始第二次深度优先遍历，顺序为2-6-3-4-8-7或者2-6-7-3-4-8等等，遍历的结果并不唯一，这取决于用户输入节点的顺序。
  广度优先遍历则类似二叉树的层序遍历，从节点1开始，则检查1的出口临近所有节点，2和5，然后检查2和5的临近节点6…，每次都需要把当前节点所有的出临近节点优先访问，则顺序可为1-5-2-6-3-7-4-8，顺序也不唯一。

python实现

import numpy as np
from collections import deque


class G:
    # mt=1,邻接矩阵,mt=0,邻接表
    def __init__(self, graph, info, mt=1):
        self.graph = graph
        self.info = info
        self.mt = mt


def visit(elem):
    print(elem)


def get_next_vertx(graph, j):
    if graph.mt == 1:
        for i in enumerate(graph.graph[j]):
            if i[1]:
                yield i[0]
            else:
                continue
    elif graph.mt == 0:
        for i in graph.graph[j]:
            yield i


def dfs(graph, index, flag=1):
    global visited
    if flag:
        flag = 0
        visited = [0] * len(graph.graph)
    if not visited[index]:
        visited[index] = 1
        visit(graph.info[index])
        for i in get_next_vertx(graph, index):
            if not visited[i]:
                dfs(graph, i, flag)
    for i in range(len(graph.graph)):
        if not visited[i]:
            dfs(graph, i, flag)


def bfs(graph, index):
    visited = [0] * len(graph.graph)
    q = deque([index])
    visited[index] = 1
    while q:
        elem = q.popleft()
        visit(graph.info[elem])
        for i in get_next_vertx(graph, elem):
            if not visited[i]:
                visited[i] = 1
                q.append(i)
    for i in range(len(graph.graph)):
        if not visited[i]:
            bfs(graph, i)


if __name__ == '__main__':
    info = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
    matric = np.array([[0, 1, 0, 0, 1, 0, 0, 0],
                       [1, 0, 0, 0, 0, 1, 0, 0],
                       [0, 0, 0, 1, 0, 1, 1, 0],
                       [0, 0, 1, 0, 0, 0, 1, 1],
                       [1, 0, 0, 0, 0, 0, 0, 0],
                       [0, 1, 1, 0, 0, 0, 1, 0],
                       [0, 0, 1, 1, 0, 1, 0, 1],
                       [0, 0, 0, 1, 0, 0, 1, 0]], dtype=bool)
    glist = [[1, 4], [0, 5], [3, 5, 6], [2, 6, 7], [0], [1, 2, 6], [5, 2, 3, 7], [3, 6]]
    Graph = G(glist, info, 0)
    bfs(Graph, 0)