【群智能算法】哈里斯鹰优化算法 HHO算法【Matlab代码#19】

文章目录

【获取资源请见文章第6节：资源获取】

1. 算法简介

HHO算法通过模仿哈里斯鹰的群体狩猎行为和突袭围捕策略实现优化算法的全局寻优，其捕猎过程分为全局探索和局部开发两个阶段。
哈里斯鹰优化算法（Harris’ Hawk Optimization，简称HHO）是一种基于鹰的行为策略的启发式优化算法。该算法模拟了鹰群中鹰之间的合作行为，通过模拟狩猎过程来寻找最优解。

HHO算法的工作原理如下：

初始化鹰的位置和速度，这些位置和速度代表了解空间中的候选解。
计算每只鹰的适应度值，适应度值代表了候选解的优劣程度。
根据适应度值选择一只"领导鹰"，通常是适应度最好的鹰。
根据一定的概率，随机选择其他鹰作为"跟随鹰"，这些鹰将采用领导鹰的行动策略。
根据鹰的行为策略（如搜索、追捕、聚集等），更新鹰的位置和速度。
判断是否达到终止条件，如果满足则输出最优解；否则返回步骤2。
HHO算法通过模拟鹰群的协作行为，将优化问题转化为搜索过程，并通过迭代来逐步改进解的质量。相比于传统的优化算法，HHO算法具有以下优点：

多样性：HHO算法通过引入随机选择的"跟随鹰"，增加了解空间的多样性，有助于避免陷入局部最优解。
协作性：领导鹰和跟随鹰之间的协作有助于信息共享和全局搜索，有助于更快地找到最优解。
简单性：HHO算法的实现相对简单，易于理解和应用。
然而，需要注意的是，HHO算法并不是适用于所有类型的优化问题，其性能可能受到问题特性的影响。在实际应用中，需要根据具体问题的特点选择合适的优化算法。

2. 探索行为

在这里插入图片描述

3. 开发行为

在这里插入图片描述

4. 部分代码展示

 %% Exploitation:
 % Attacking the rabbit using 4 strategies regarding the behavior of the rabbit
 
 %% phase 1: surprise pounce (seven kills)
 % surprise pounce (seven kills): multiple, short rapid dives by different hawks
 
 r=rand(); % probablity of each event
 
 if r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiege
     X(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-X(i,:));
 end
 
 if r>=0.5 && abs(Escaping_Energy)>=0.5  % Soft besiege
     Jump_strength=2*(1-rand()); % random jump strength of the rabbit
     X(i,:)=(Rabbit_Location-X(i,:))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-X(i,:));
 end

5. 仿真图展示

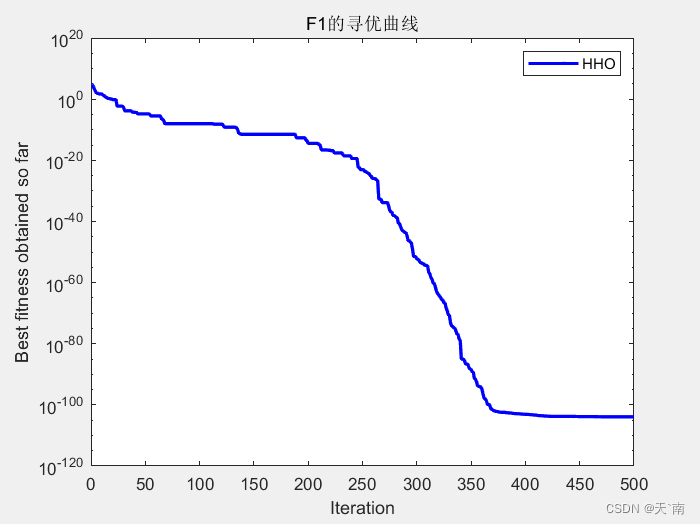
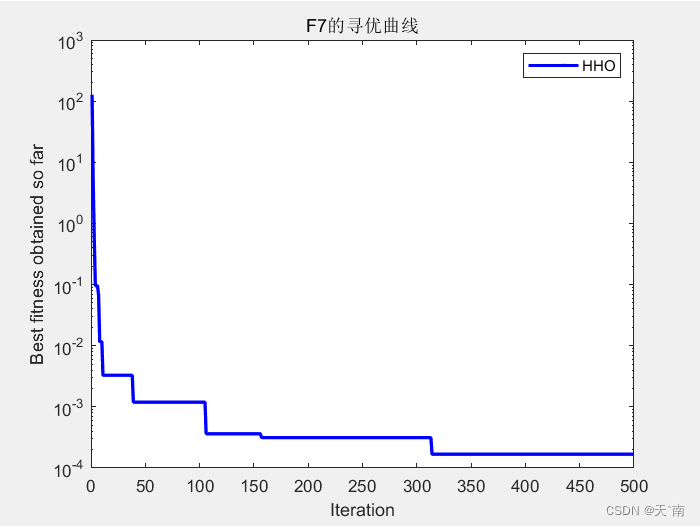
在这里插入图片描述
在这里插入图片描述

6. 资源获取

可以获取完整代码资源。