基于A*算法的路径规划实践(MATLAB语言)
基于A*算法的路径规划实践
1. 机器人路径优化问题描述
1.1 机器人路径优化问题综述
路径最优规划是移动机器人系统中最重要的组成部分之一,分为点到点的路径规划和全覆盖路径规划。点到点的路径规划是按照走路线最短、行走时间最短等一定的评价标准进行,在其工作空间中找到一条从起始点到目标点的能避开障碍物的最优路径。根据是否给定全局的环境可主要划分为全局路径规划和局部路径规划。本文主要研究给定环境下进行的路径的规划,在进行全局路径规划过程中,要找到一条从起点到终点的最优路径,首先进行整体环境建模,在此基础上通过搜索算法进行最短路径规划。
在给定环境的情况下需要对全局环境进行建模,环境建模方法通常有栅格法、机器视觉法和拓扑图法等,在进行环境建模时通常采用其中一种或多种方法结合的建模方法。其中栅格法是最常见的建模方法,通过给定的环境进行栅格量化机器人和障碍物位置可以用栅格的坐标来描述,编程易实现。
1.2 环境建模方法
环境建模方法通常有机器视觉法、拓扑图和法栅格法等。
机器视觉法是机器人将采集到的环境地图信息发送给计算机终端,计算机对图像进行分析处理与识别,将结果反馈给机器人,其优点处理精度高,处理内容丰富,可进行复杂的非线性处理, 有灵活的变通能力, 一般来说只要改变软件就可以改变处理内容。其缺点是处理速度还是一个问题, 特别是进行复杂的处理更是如此。
栅格法是将机器人和工作环境量化在相邻单元的小格中,并建立坐标。机器人初始位置置于起点处,以机器人为中心形成上、下、左、右、左上、左下、右上、右下的八连通栅格。连接机器人栅格顶点到障碍物外可视顶点形成可视线,这样从起点到目标点就有多条可搜索路径。
1.3 机器人路径优化解决方法
现在对于一直工作环境的路径规划常见的算法有遗传算法、粒子群算法、蚁群算法、人工势场法、模糊规则法、神经网络、模拟退火算法、快速扩展随机树、A-Star算法等。这些算法各有特点,有优点也有缺点。这些方法大部分都需要在一个确定的空间内对障碍物进行建模,计算复杂度与机器人自由度呈指数关系,并通过对状态空间中的采样点进行碰撞检测,来路径规划问题。本文主要采用对A-Star算法改进进行对路径进行优化,并会与其他的一种方法进行比较。
2. A*算法介绍
2.1 算法综述
A-Star算法是一种基于启发式搜索的一种最好优先的算法,同时又加上了一些约束条件。在状态空间中,对每一个要搜索的位置进行评估,得到最好的位置。再以这个位置进行搜索,直到到达目标位置。这样可以减少搜索范围,降低问题复杂度,从而提高了效率。在启发式搜索中,对位置的估价,需要用到估价函数,这是十分重要的。启发式搜索在搜索的过程中选取“最佳节点”后舍弃其他的兄弟节点,父亲节点,而一直得搜索下去。这种搜索的结果很明显,由于舍弃了其他的节点,可能也把 最好的节点都舍弃了。但A-Star在搜索时,便没有舍弃节点(除非该节点是死节点),在每一步的估价中 都把当前的节点和 以前的节点的估价值比较得到一个“最佳的节点”。这样可以有效的防止“最佳节点”的丢失。
总的来说A-Star算法能够高效快速的解决路径规划问题,在寻找最优路径时间上都较其他算法快速。
2.2 A-Star算法步骤
A-Star用到一种估计函数,公式表示为:f(n)=g(n)+h(n),其中,f(n)是从初始状态经由状态n到目标状态的代价估计,g(n)是在状态空间中从初始状态到状态n的实际代价,h(n)是从状态n到目标状态的最佳路径的估计代价。(对于路径搜索问题,状态就是图中的节点,代价就是距离)。
其运算步骤如下:
- 把起点加入open列表中
- 遍历open列表中,找到F值最小的节点,把它作为当前处理的节点,并把该节点加入close列表中。
- 对该节点的8个相邻格子进行判断,如果格子是不可抵达的或者在close列表中,则忽略它,否则如下操作:
a. 如果相邻格子不在open列表中,把它加入,并将parent设置为该节点和计算f,g,h值
b. 如果相邻格子已在open列表中,并且新的G值比旧的G值小,则把相邻格子的parent设置为该节点,并且重新计算f值。 - 重复2,3步,直到终点加入了open列表中,表示找到路径;或者open列表空了,表示没有路径。
如果开启列表已经空了,说明路径不存在。 - 最后从目标格开始,沿着每一格的父节点移动直到回到起始格,这就是路径。
3.A-Star算法求解机器人路径优化
3.1 环境建模
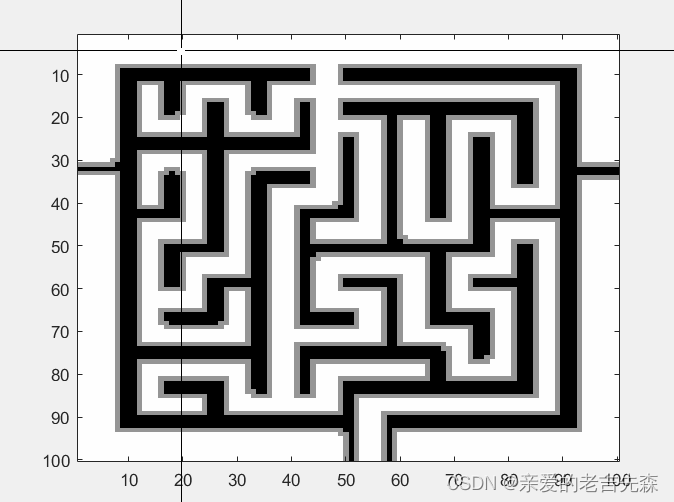
本文采用栅格法建模,从文件中读取bmp格式图片先将其灰度化,然后将其转化成一个nn的环境区域,即将图片划分成nn个像素块。并且显示的图像上有x,y坐标轴的显示,可以看到图像的像素大小。图片中障碍物转化为灰色像素块,并用0表示;无障碍物的转化为白色像素块,并用1表示。
3.2 基本思路
在全局路径规划中,机器人从起点开始到节点再从节点到目标点的代价值用遍历的栅格总和来表示,也就是机器人每覆盖一个栅格,成本代价就是从起点到节点的覆盖栅格数的累加,估计代价就是从当前节点到目标点的栅格数累加。机器人在覆盖栅格的时候首先要判断目标栅格是否是自由栅格,然后判断这个自由栅格是否是关联性最大的栅格,与相关栅格比较如果关联值最大即作为覆盖栅格。如果关联属性值大小一样,在机器人的八连通方向上按照顺时针栅格。
3.3 路径规划流程
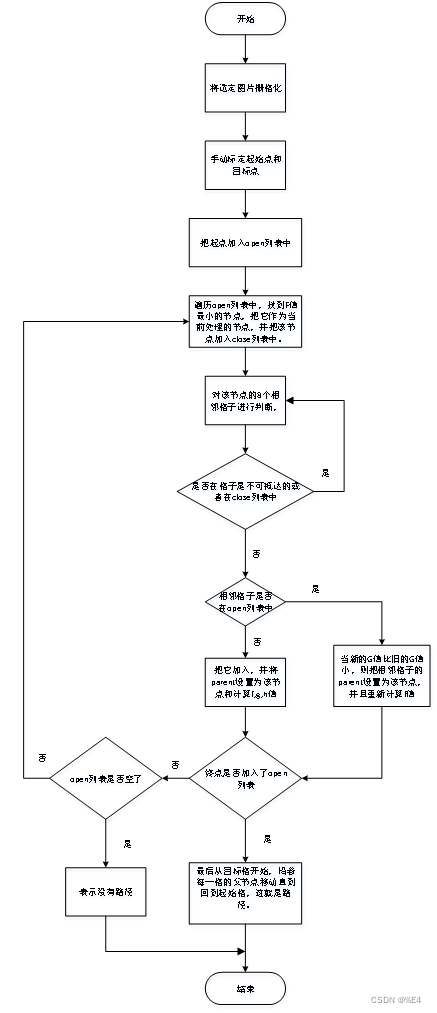
3.4 A-Star算法的改进方向
根据全局环境这个条件,可设计双向搜索的方式,即起始点和目标点同时搜索,当从两点搜索到同一坐标时,连接两边搜索过的最短路径,即为要求的路径。这样可节约搜索时间,提高路径规划效率,但是否为最短路径,还需要仿真实验来验证。
4. 总结
仿真结果证明本文提出的A-Star算法大幅缩小了排查节点的范围,提高了计算效率和寻路过程中的方向性,使得找点更趋向于终点,且利用栅格化的环境建模方法能很好地处理复杂的平面地形,便于算法进行处理。且该设计可改变栅格地图起点和终点的设置,都能实现路径规划。。仿真实验结果表明该方法具有可行性和有效性,该设计使路径规划能够获得较优路线。
5. 代码
5.1 文件主函数
%%下载地图并初始化参数
figure(1)
mapOriginal=imbinarize(imread('Maps/Map (9).bmp')); %从bmp文件读取地图
resolutionX=100;
resolutionY=100;
mapResized=imresize(mapOriginal,[resolutionX resolutionY]);
map=mapResized;
%连接矩阵-定义机器人可允许的动作
conn=[1 1 1;
1 2 1;
1 1 1];
display_process=true; %显示节点的处理
% 增加一个单位像素的边界——考虑到机器人的大小
for i=1:size(mapResized,1)
for j=1:size(mapResized,2)
if mapResized(i,j)==0
if i-1>=1, map(i-1,j)=0; end
if j-1>=1, map(i,j-1)=0; end
if i+1<=size(map,1), map(i+1,j)=0; end
if j+1<=size(map,2), map(i,j+1)=0; end
if i-1>=1 && j-1>=1, map(i-1,j-1)=0; end
if i-1>=1 && j+1<=size(map,2), map(i-1,j+1)=0; end
if i+1<=size(map,1) && j-1>=1, map(i+1,j-1)=0; end
if i+1<=size(map,1) && j+1<=size(map,2), map(i+1,j+1)=0; end
end
end
end
image((map==0).*0 + (map==1).*255 + (mapResized-map).*150);
colormap(gray(256))
%选出初始点和目标点
disp('select source in the image');
[x,y] = ginput(1);
source=[double(int8(y)) double(int8(x))]; % source position in Y, X format
disp('select goal in the image');
[x,y] = ginput(1);
goal = [double(int8(y)) double(int8(x))]; % goal position in Y, X format
if length(find(conn==2))~=1, error('no robot specified in connection matrix'); end
%% Compute path
%节点的结构被认为是位置、位置、历史成本、启发式成本、总成本、封闭列表中的父索引
Q=[source 0 heuristic(source,goal) 0+heuristic(source,goal) -1]; %A*算法的处理队列,开放列表
closed=ones(size(map)); % 黑色已标记存到闭列表
closedList=[]; % the closed list taken as a list
pathFound=false;
tic;
counter=0;
size(Q)
while size(Q,1)>0
[A, I]=min(Q,[],1);
n=Q(I(5),:); % 过程最小成本元素
Q=[Q(1:I(5)-1,:);Q(I(5)+1:end,:)]; % 删除正在处理中的元素
if n(1)==goal(1) && n(2)==goal(2) %目标测试
pathFound=true;break;
end
[rx,ry,rv]=find(conn==2); %连接矩阵中的机器人位置
[mx,my,mv]=find(conn==1); %可能移动的数组
for mxi=1:size(mx,1) %遍历所有的移动
newPos=[n(1)+mx(mxi)-rx n(2)+my(mxi)-ry]; %可能的新节点
if checkPath(n(1:2),newPos,map) %如果从n到newPos的路径是无碰撞的
if closed(newPos(1),newPos(2))~=0 %还没有关闭
historicCost=n(3)+historic(n(1:2),newPos);
heuristicCost=heuristic(newPos,goal);
totalCost=historicCost+heuristicCost;
add=true; %还没有在更好的代价下排好队
if length(find((Q(:,1)==newPos(1)) .* (Q(:,2)==newPos(2))))>=1
I=find((Q(:,1)==newPos(1)) .* (Q(:,2)==newPos(2)));
if Q(I,5)<totalCost, add=false;
else Q=[Q(1:I-1,:);Q(I+1:end,:);];add=true;
end
end
if add
Q=[Q;newPos historicCost heuristicCost totalCost size(closedList,1)+1]; %在队列中添加新节点
end
end
end
end
closed(n(1),n(2))=0;closedList=[closedList;n]; %更新闭列表
i0 = counter;
i1 = 40;
counter=counter+1;
if display_process == true && (rem(i0,i1) == 0)
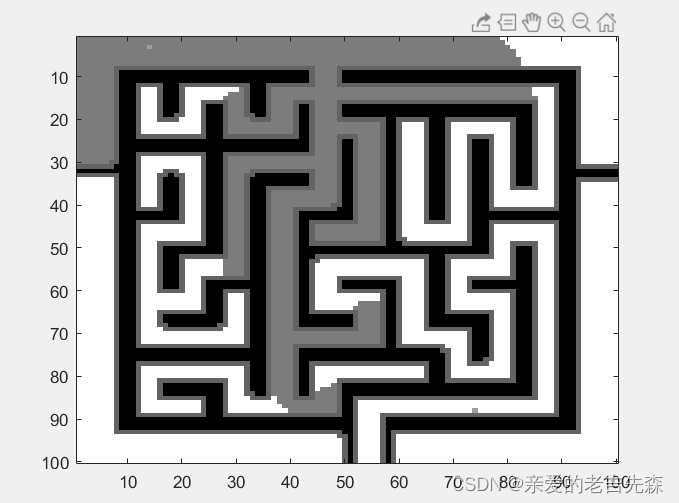
temp_img = (map==0).*0 + ((closed==0).*(map==1)).*125 + ((closed==1).*(map==1)).*255 + (mapResized - map).*100 ;
%画出目标和起始点
temp_img(goal(1), goal(2) ) = 160;
temp_img(source(1), source(2) ) = 160;
image(temp_img);
M(counter)=getframe;
end
size(Q)
end
if ~pathFound
error('no path found')
end
%% Plot complete path绘制完整路线
figure(2)
path=[n(1:2)]; %从源信息检索路径
prev=n(6);
while prev>0
path=[closedList(prev,1:2);path];
prev=closedList(prev,6);
end
path=[(path(:,1)*size(mapOriginal,1))/resolutionX (path(:,2)*size(mapOriginal,2))/resolutionY];
pathLength=0;
for i=1:length(path)-1, pathLength=pathLength+historic(path(i,:),path(i+1,:)); end
fprintf('processing time=%d \nPath Length=%d \n\n', toc,pathLength);
imshow(mapOriginal);
line(path(:,2),path(:,1));
5.2 checkPath.m
function feasible=checkPath(n,newPos,map)
feasible=true;
dir=atan2(newPos(1)-n(1),newPos(2)-n(2));
for r=0:0.5:sqrt(sum((n-newPos).^2))
posCheck=n+r.*[sin(dir) cos(dir)];
if ~(feasiblePoint(ceil(posCheck),map) && feasiblePoint(floor(posCheck),map) && ...
feasiblePoint([ceil(posCheck(1)) floor(posCheck(2))],map) && feasiblePoint([floor(posCheck(1)) ceil(posCheck(2))],map))
feasible=false;break;
end
if ~feasiblePoint(newPos,map), feasible=false; end
end
5.3 feasiblePoint.m
function feasible=feasiblePoint(point,map)
feasible=true;
% check if collission-free spot and inside maps
if ~(point(1)>=1 && point(1)<=size(map,1) && point(2)>=1 && point(2)<=size(map,2) && map(point(1),point(2))==1)
feasible=false;
end
5.4 heuristic.m
function h=heuristic(X,goal)
h = sqrt(sum((X-goal).^2));
5.5 historic.m
function h=historic(a,b)
h = sqrt(sum((a-b).^2));
6. 效果图