算法基础部分6-贪心算法
算法部分 基础6
一、贪心算法简述
贪心算法的每一步行动总是按照某种指标选取最优的操作来进行该指标,只看眼前并不考虑以后可能造成的影响。证明方法通过替换法和数学归纳法实现。
二、贪心算法例子
1. 圣诞老人的礼物
问题描述:圣诞节来临了,中圣诞老人准备分发糖果,现在有多箱不同的糖果,每箱糖果都有自己的价值和重量,每箱糖果都可以拆分成任意散装组合带走。圣诞老人的驯鹿雪橇最多只能装下重量为 W 的糖果,请问圣诞老人最多能带走多大价值的糖果。
输入:第一行由两个部分组成,分别为糖果箱数正整数 n (1 <= n <= 100),
驯鹿能承受的最大重量正整数 w (0 < w < 10000), 两个数用空格隔开。其余
n 行每行对应一箱糖果,由两部分组成,分别为一箱糖果的价值正整数 v 和重量
正整数 w , 中间用空格隔开。
输出:输出为圣诞老人能带走的糖果的最大总价值,保留 1 位小数。输出为一
行,以换行符结束。
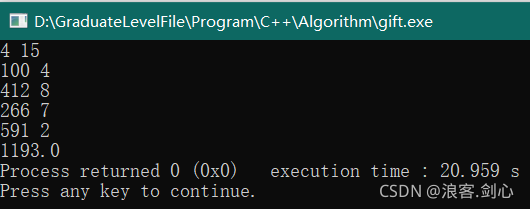
样例输入
输入:
4 15
100 4
412 8
266 7
591 2
输出:
1193.0
分析和程序如下
按礼物的价值/重量比从大到小一次选取礼物,对选取的礼物尽可能地多装,直到
重量为 w , 复杂度 O(nlogn).
程序如下:
#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
const double eps = 1e-6;
struct Candy{
int v; int w;
}candies[110];
//箱子按单位重量价值排序
bool operator < (const Candy & a, const Candy & b) {
return float(a.v) / a.w - float(b.v) / b.w > eps;
}
int main(){
int n, w;
scanf("%d%d", & n, & w);
for(int i = 0; i < n; i++){
scanf("%d%d", & candies[i].v, & candies[i].w);
}
sort(candies, candies + n);
int totalW = 0;
double totalV = 0;
// 排好序,按照顺序取就行
for(int i = 0; i < n; i++){
if(totalW + candies[i].w <= w){
totalW += candies[i].w;
totalV += candies[i].v;
}else{
totalV += candies[i].v *
double(w - totalW) / candies[i].w;
break;
}
}
printf("%.1f", totalV);
return 0;
}
结果如下,
对于这个题,若糖果只能整箱拿,则贪心法得到结果是错误的。考虑以下例子,只能整箱拿, 3 个箱子 (8, 6), (5, 5), (5, 5), 雪橇总容量为 10 。如果按照贪心算法,拿的是 (8, 6) ,就不能拿了。但是 (5, 5), (5, 5) 是最优的。
2. 电影节
问题描述:大学生电影节在北大举办!这天,在北大各地放了多部电影,给定每部电影的放映时间区间,区间重叠的电影不可能同时看(端点可以重合),问李雷最多可以看多少部电影。
输入:多组数据。每组数据开头都是 n (n <= 100), 表示共 n 场电影,接下
来 n 行,每行两个整数 (均是小于 1000) , 表示一场电影的放映区间,n = 0
则数据结束。
输出:对每组数据输出最多能看几部电影
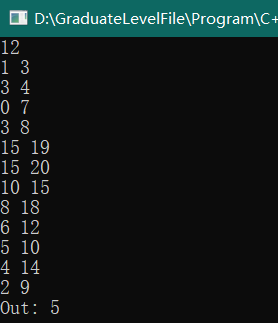
样例如下
输入:
12
1 3
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
5 10
4 14
2 9
输出:
5
分析
贪心解法:
将所有电影按结束时间从小到大排序,第一步结束时间最早的那部电影。然
后,每步都选和上一部选中的电影不冲突且结束时间最早的电影。
复杂度:O(nlogn)
程序如下
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
struct Film{
int starts;
int ends;
}a[100];
// 使用快速排序需要一种比较方式
// void * 类型指针可以强制转化为任何类型指针
int cmp(const void * a,const void * b){
struct Film * pa = (struct Film *) a;
struct Film * pb = (struct Film *) b;
if( pa -> ends >= pb -> ends) return 1;
else return -1;
}
int main(){
int n;
int numFilm;
int endTime;
scanf("%d", & n);
while(n != 0){
int i = 0;
for(i = 0; i < n; i++){
scanf("%d%d", & a[i].starts, & a[i].ends);
}
// 使用快排,用 cmp 函数作为比较方式
qsort(a, n, sizeof(a[0]), cmp);
numFilm = 1;
endTime = a[0].ends;
for(i = 1; i < n; i++){
if(a[i].starts >= endTime){
numFilm ++;
endTime = a[i].ends;
}
}
printf("Out: %d\n", numFilm);
}
return 0;
}
结果如下
这个也比较好理解,通过对电影放映结束时间进行排序,这样的策略来实现贪心算法。
3. 分配畜栏
有 n 头牛 (1 <= n <= 50, 000) 要挤奶。给定每头牛挤奶的时间区间 [A, B] (1 <= A <= B <= 1, 000, 000,A,B 为整数) 。
牛需要待蓄栏同一时间只能容纳一头牛。问至少需要多少个蓄栏,才能完成全程挤奶工作,以及每头牛都放在哪个蓄栏里。
去同一个蓄栏的两头牛,它们挤奶时间区间哪怕只在端点重合也是不可以的。
分析
所有奶牛都必须挤奶。到了一个奶牛的挤奶开始时间,就必须为这个奶牛找畜栏。因此按照奶牛
的开始时间逐个处理它们,是必然的。
S(x) 表示奶牛 x 的开始时间。E(x) 表示 x 的结束时间。对 E(x), x 可以是奶牛,也可
以是畜栏。畜栏的结束时间,就是正在其里面挤奶的奶牛的结束时间。同一个畜栏的结束时间是
不断在变的。
1) 把所有奶牛按开始时间从小到大排序。
2) 为第一头奶牛分配一个畜栏。
3) 依次处理后面每头奶牛 i 。处理 i 时,考虑已分配畜栏中,结束时间最早的畜栏 x .
若 E(x) < S(i) , 则不用分配新畜栏,i 可进入 x , 并修改 E(x) 为 E(i)
若 E(x) >= S(i) , 则分配新畜栏 y ,记 E(y) = E(i)
直到所有奶牛结束
需要用优先队列存放已经分配的畜栏,并使得结束时间最早的畜栏始终位于队列头部。
复杂度 O(nlogn)
程序如下,
#include <stdlib.h>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
struct Cow{
int startT, endT; // 挤奶区间, 开始时间和结束时间
int No; // 编号
// 定义结构体比较大小的方式
bool operator < (const Cow & c) const {
return startT < c.startT;
}
} cows[50100];
int pos[50100]; // pos[i] 表示标号为 i 的奶牛去的畜栏编号
// 畜栏结构体
struct Stall{
int ends; // 结束时间
int No; // 编号
bool operator < (const Stall & s) const {
return ends > s.ends;
}
Stall(int e, int n): ends(e), No(n){ }
};
int main(){
int n;
scanf("%d", & n);
for(int i = 0; i < n; i++){
scanf("%d%d", & cows[i].startT, & cows[i].endT);
cows[i].No = i;
}
sort(cows, cows + n);
int total = 0;
// 在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。
priority_queue <Stall> pq;
for(int i = 0; i < n; i++){
// 队列代表的是畜栏的个数,FIFO
if( pq.empty() ){
total++;
pq.push(Stall(cows[i].endT, total));
pos[cows[i].No] = total; // 某个牛被安排在第 total 的畜栏
}else{
// 返回 结束时间 最大的畜栏
Stall st = pq.top(); // 优先队列能够把最大的放在最上面
if(st.ends < cows[i].startT){
pq.pop();
pos[cows[i].No] = st.No;
pq.push(Stall(cows[i].endT, st.No));
}else{ // st.ends > cows[i].startT
// 开辟新的畜栏
total++;
pq.push(Stall(cows[i].endT, total));
pos[cows[i].No] = total;
}
}
}
printf("Stall num: %d\n", total);
for(int i = 0; i < n; i++){
printf("Cow %d in %d stall.\n", i, pos[i]);
}
return 0;
}
运行结果如下,
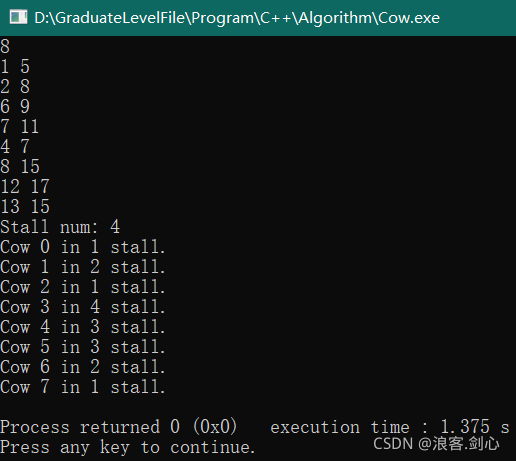
程序分析,
1.
定义两个结构体:
struct Cow 定义了每头牛开始挤奶时间和结束时间,并对牛编号
struct Stall 定义了每个畜栏中编号为 i 的牛结束的时间,并且该牛占用到时间结束
并且两个结构体都对运算符 < 进行了重载,方便比较。
2.
// 注意 Cow 对小于号的重载,是对结束时间进行比较
sort(cows, cows + n); // 使用排序的方法,对牛按照结束时间从小到大排序
3.
// 注意 Stall 对小于号重载,是对结束时间进行比较,所以结束时间最短的在队头
// 注意,是对 < 重载, return ends > s.ends; 返回是大于号,结束时间最短的在队头
priority_queue <Stall> pq; // 使用优先队列,让结束时间最短的在队头。
4.
// 返回 结束时间 最小的畜栏,Stall 对运算符进行了重载
Stall st = pq.top(); // 优先队列能够把优先级最大的放在最上面
// 如果最小的完成了,那新的牛进入队列
if(st.ends < cows[i].startT){
pq.pop();
// 返回已有畜栏的编号
pos[cows[i].No] = st.No;
pq.push(Stall(cows[i].endT, st.No));
}else{ // st.ends > cows[i].startT
// 开辟新的畜栏
total++;
pq.push(Stall(cows[i].endT, total));
pos[cows[i].No] = total;
}
这个程序难点和要点是对优先队列的使用和运算符重载,使用的是贪心算法,这个题还是比较有意思的。
4. 安装雷达
x 轴是海岸线,x 轴上方是海洋。海洋中有 n (1 <= n <= 1000) 个岛屿,可以看作点。
给定每个岛屿的坐标 (x, y) , x, y 都是整数。
当一个雷达 (可以看作点) 到岛屿的距离不超多 d (整数), 则认为该雷达覆盖了该岛屿。
雷达只能放在 x 轴上。问至少需要多少个雷达才可以覆盖全部岛屿。
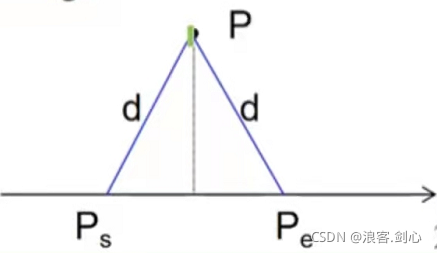
如图,
分析如下,
对于每个岛屿 P , 可以算出,覆盖它的雷达,必须位于 x 轴上的区间 [Ps, Pe].
如果有雷达位于某个 x 轴区间 [a, b], 称该雷达覆盖此区间。问题转换为,至少要在 x 轴
上放几个雷达 (点) , 才能覆盖全部区间 [P1s, P1e], [P2s, P2e] ... [Pns, Pne].
重要结论:
如果可以找到一个雷达同时覆盖多个区间,那么把这多个区间按起点坐标从小到大排序,则最后
一个区间(起点靠右的) k 的起点,就能覆盖所有区间。
所以只用找区间的起点来放置雷达
输出方式
输入:输入包含若干组数据,每组数据的第一行是两个整数 n 和 d (1 <= n <= 1000), 分
别表示小岛的数量和雷达的半径。接下来有 n 行, 每行的两个整数分别表示各个小岛的坐标。
输入以 0 0 结束。
输出:对于每组数据输出一行,为最少的雷达数,如果该组数据无解,则输出 -1 .
输出样例
输入:
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
输出:
case 1: 2
case 2: 1
程序如下
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
#define MAXN 1010
// 雷达在[Psi, Pei] 可以探测到改点
struct Node{
double left, right;
};
int T, n, d;
Node s[MAXN];
// 比较左边节点,找到最后一个满足可以覆盖前面一组的点
bool operator < (const Node & a, const Node & b){
return a.left < b.left;
}
// 求解每个 case
int Solve(){
int ans = 1; // 雷达个数
double now; // 标记能够覆盖的点
// 按左端点排序
sort(s, s + n);
// 若当前线段与目前集合中的线段没有交集,则加入一个新雷达
now = s[0].right;
for(int i = 1; i < n; i++){
if(s[i].left <= now) now = min(now, s[i].right);
else{
ans++;
now = s[i].right;
}
}
return ans;
}
int main(){
int x, y;
bool flag;
T = 0;
while(true){
T++;
// 雷达总数和雷达半径
scanf("%d%d", & n, & d);
if(n == 0 && d == 0) break;
// 读入
flag = true;
for(int i = 0; i < n; i++){
// x, y 是坐标
scanf("%d%d", & x, & y);
if(y > d) flag = false;
else{
// 勾股定理计算该点雷达可以检测两端点
s[i].left = x - sqrt(d * d - y * y);
s[i].right = x + sqrt(d * d - y * y);
}
}
// 若有小岛距离 x 轴大于 d , 则输出 -1
if(flag) printf("Case %d: %d\n", T, Solve());
else printf("Case %d: -1\n", T);
}
return 0;
}
结果如下
这个程序比较好理解,主要是上面分析过程,关于数学逻辑和推导。感觉贪心算法主要是考虑数学逻辑和对问题分析能力。
三、总结
现在程序设计与算法部分一,二,三全部刷完了。现在开始正式入门 C++ ,后面算法会继续刷着,我觉得精彩,难理解的会在博客分享。后面应该记录周期会长一些了。不过依旧会坚持更新,深入深入!