二叉搜索树:红黑树的原理和实现
前言
💭上文我们在遇到问题:二叉搜索树退化到单支导致效率和性能降低时,利用了AVL树解决。但是由于AVL树是一棵绝对平衡的树,每次修改树结构都要保证左右子树高度差的绝对值不超过1,这可能会引发多次旋转。因此,若我们要设计出一棵结构动态变化的二叉搜索树,利用AVL树的效率并不高。基于这个原因,红黑树诞生了。
1. 红黑树的概念
🔴⚫
红黑树(RBTree)是一种二叉搜索树,在每个节点设置一个存储域用于指明该节点的颜色(Red或Black),进而,通过限制任一条从根到叶子节点的路径上的各个节点的着色方式,使得任一条路径的长度都不超过另一条路径,最终达到接近平衡的树结构。
📃红黑树结构示意图:
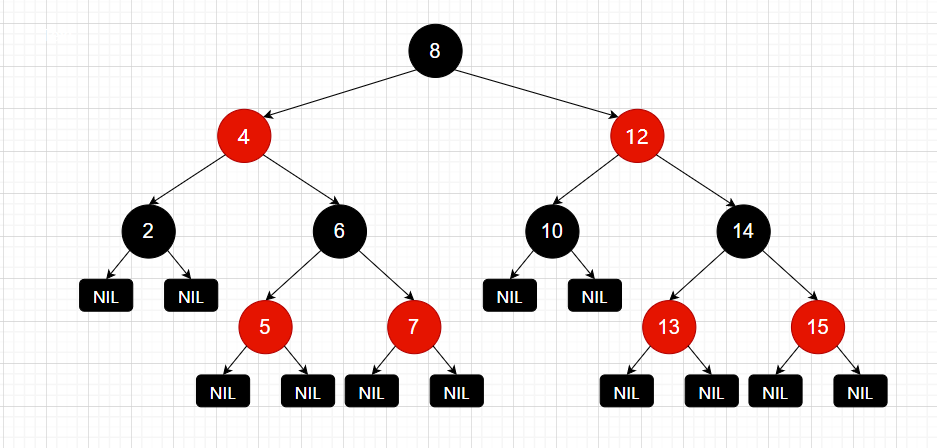
其中,NIL为空节点
2. 红黑树的性质
每一棵红黑树,都满足以下五条性质:
- 每个节点不是黑色就是红色
- 根节点为黑
- 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点
- 不允许有相邻的两个红色节点
- 每个叶节点都为黑(此处的叶节点指
NIL节点)
💡这五条性质,保证了红黑树最长路径长度不超过最短路径长度的二倍。
- 为何要引进 NIL 节点?
保证任意节点都有两个分叉,这样才能使得红黑树接近平衡。不这样做的话,若直接以平时的叶子节点作叶节点,极端情况下,下面这棵树同样满足红黑树的性质,但是其已经退化成链表了,查找效率为O(N)。
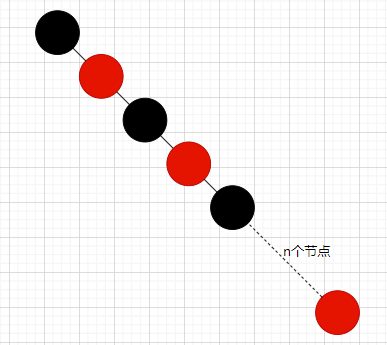
- 如何保证最长路径长度不超过最短路径的二倍?
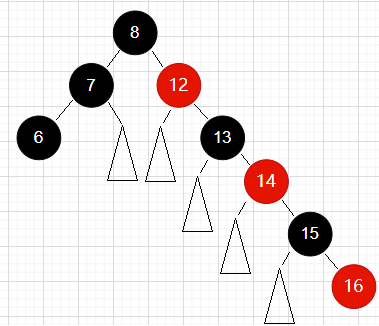
如图所示,我们以8为根节点的红黑树为例(只关注左右两条路径,假设左路径是最短路径,右路径是最长路径,图中三角形是一些能保证整棵树为红黑树的不同情况的子树)
由性质3可得,最短路径中的黑节点必须与最长路径中的黑节点数量相同,又由性质4,最终可得最短路径节点全为黑,且与最长路径中黑节点数量相同。而最长路径中,在与最短路径拥有相同数量黑节点的前提下,穿插了红色节点,使之长度最长的方法是每个黑节点都带一个红节点。这样一来,最长路径的长度就是最短路径的二倍,此时最长路径最后一个节点为红,插入红色节点违反性质4,插入黑色节点违反性质3,因此最长路径长度不超过最短路径长度的二倍。如图中,左边路径长度为3(最短),右边路径长度为6(最长)。
3. 红黑树的定义
// 枚举:红和黑
enum COLOR
{
RED,
BLACK,
};
// RBTree的节点
template <class V>
struct RBTreeNode
{
typedef RBTreeNode<V> Self;
V _v; // 数据域
Self* _left;
Self* _right;
Self* _parent;
COLOR _col; // 颜色域
RBTreeNode(const V& v)
:_v(v)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)
{}
};
// RBTree的大致结构
template <class V>
class RBTree
{
typedef RBTreeNode<V> node;
public:
RBTree()
:_root(nullptr)
{}
private:
node* _root;
};
4. 红黑树的插入操作
💭红黑树的插入,是其区别于AVL树的最大亮点,红黑树的插入减少了一些旋转,使用
变色+旋转的调整方式,提高了插入效率。
💨红黑树的插入操作可分为两步 :
- 按照二叉搜索树的规则,插入新节点
⭕ 插入新节点默认为红。如果默认为黑,则必定违反性质3,需要做的调整更多。而默认为红,有可能会违反性质4,需要做出调整,也可能不违反任何性质,无需调整。因而选择第二种方案,减少插入时的调整次数,提高效率。
template <class V>
class RBTree
{
typedef RBTreeNode<V> node;
public:
//...
bool insert(const V& v)
{
if (_root == nullptr)
{
_root = new node(v);
_root->_col = BLACK;
return true;
}
//插入
node* cur = _root;
node* parent = nullptr;
while (cur)
{
if (v < cur->_v)
{
parent = cur;
cur = cur->_left;
}
else if (v > cur->_v)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new node(v);
if (cur->_v < parent->_v)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
// ...
}
private
node* _root;
};
- 检查插入后是否破坏了红黑树结构,若是则需进行调整
💭因为新节点的默认颜色是红色,所以:
- 如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;
- 如果新插入节点的双亲节点颜色为红色时,就违反了性质3
不允许有相邻的两个红色节点,此时需要对红黑树分情况来讨论,不同情况有不同调整方法:
约定: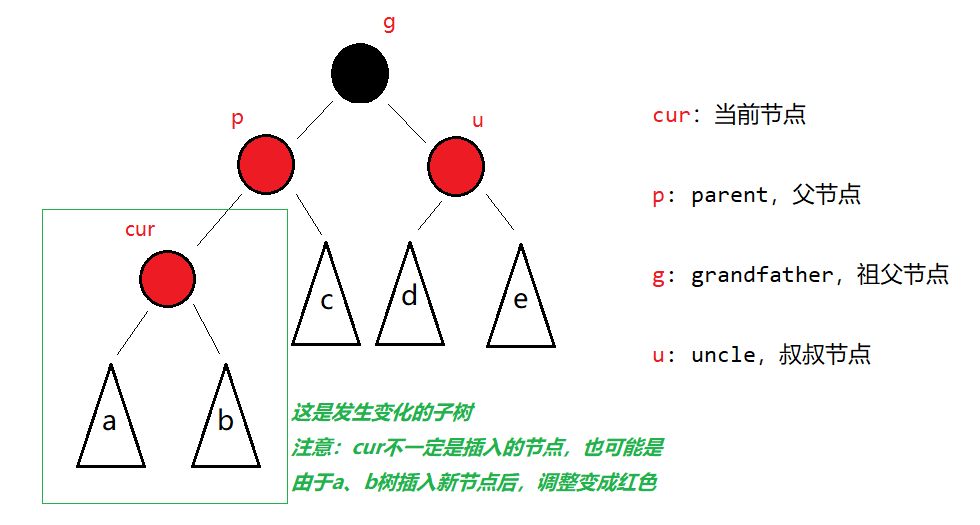
需要调整时,cur为红,p为红,g为黑(否则调整前p、g就已经破坏了红黑树的规则)。因此我们重点看uncle节点的情况,uncle节点的存在与否、着色状态决定了该如何调整。
1️⃣情况1:uncle节点存在且为红
⭕注意,此时看到的树可能是某棵子树,也有可能是整棵树。
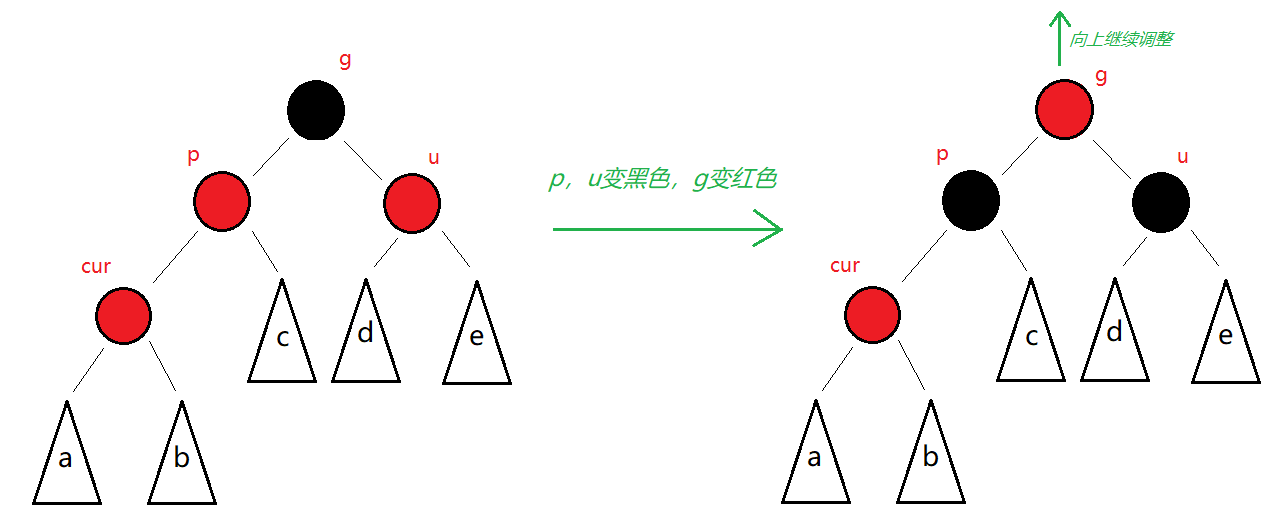
- 📝调整方法:p,u变黑,g变红。这样做不仅解决了相邻两个红节点的问题,还使得以g为根到任意叶子节点的每条路径的黑节点数量不变。但是要注意g还需继续向上调整。
为什么g还需要向上继续调整?
- 当这棵树是某棵子树时,g一定还有双亲节点,若g的双亲节点为红色,则需要继续向上调整。
- 当这棵树是整颗树时,g是根节点,则需要修改g的颜色为黑,否则会破坏性质2(根节点为黑)。
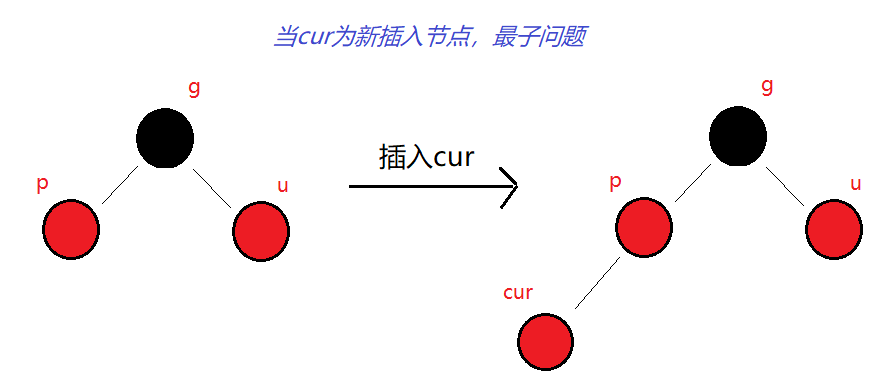
- 🔎综上所述,cur可以是新插入节点,也可以是由a、b子树插入节点调整(情况1)后变成红色。 若cur为新插入的节点,易得a、b为空树。此时c、d、e皆为空树,否则插入前的树并不是红黑树。若cur是调整后得来的红节点,则各个子树又有不同情况。总而言之,插入新节点前该树必须满足红黑树的性质。
- 因为情况1并不涉及旋转,不会调整树的物理结构,所以调整方法与cur的插入位置无关,只要满足条件即可。下面四种情况均属于情况1的调整。
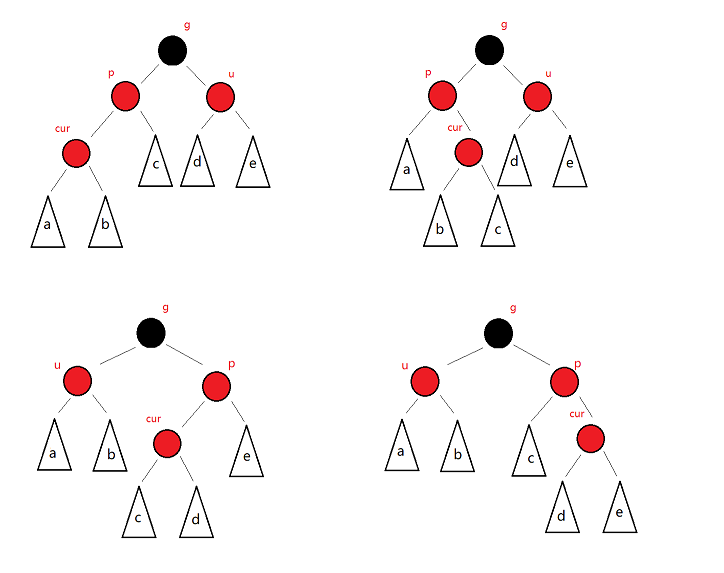
2️⃣情况2:uncle节点不存在/存在且为黑
-
uncle不存在。cur只能是新插入节点的情况(不能是由子树调整而来变红)。abcde子树均不存在,否则插入之前不满足红黑树的性质。
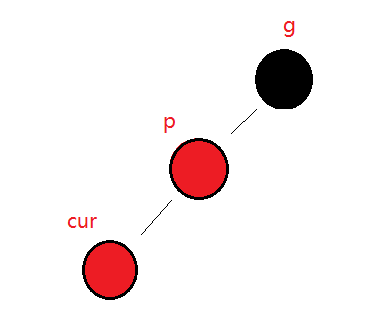
-
uncle存在且为黑。cur只能是由子树调整而来变红 (即情况1变化而来) 的情况(不能是新插入节点),否则调整前不满足红黑树的性质。
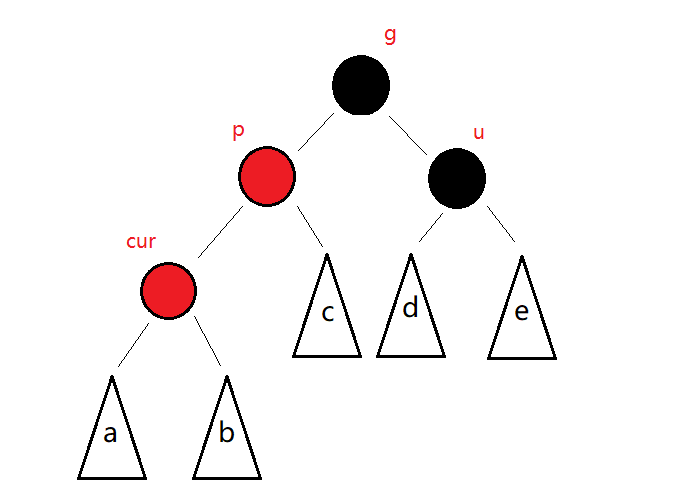
⭕假设cur为新插入节点,则插入前树结构如图所示(暂且不考虑NIL节点),违反性质3。
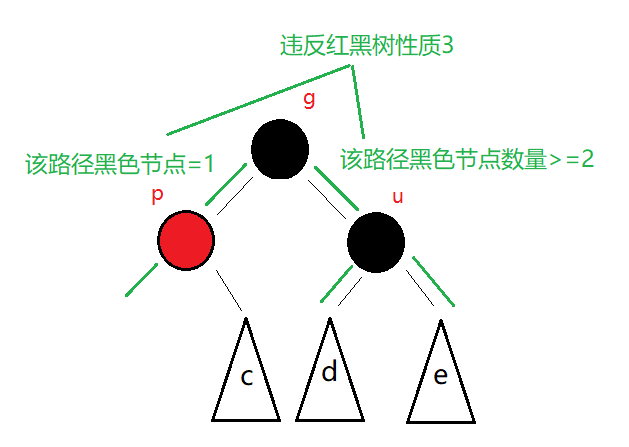
(1)(2)的调整方法都是一样的。不同于情况1,情况二无法单凭节点的变色完成调整,而是要借助旋转+变色。旋转方式与AVL树的旋转大同小异。
-
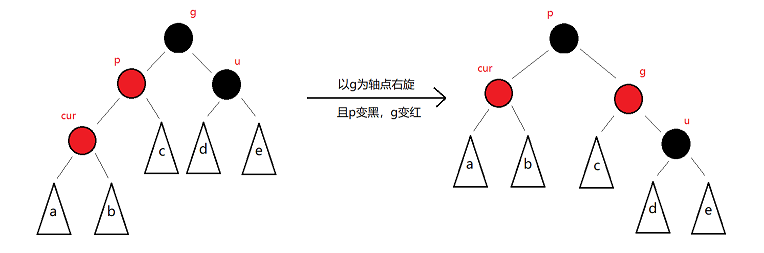
左左——右单旋
-
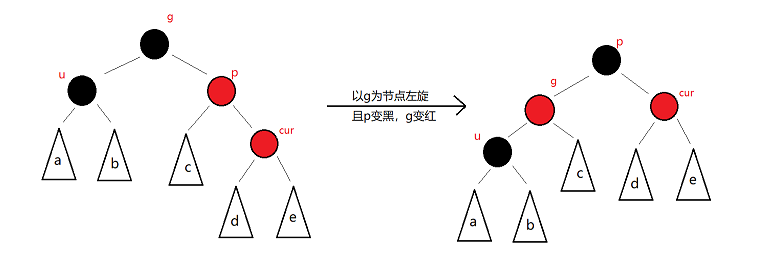
右右——左单旋
-
左右——左右双旋
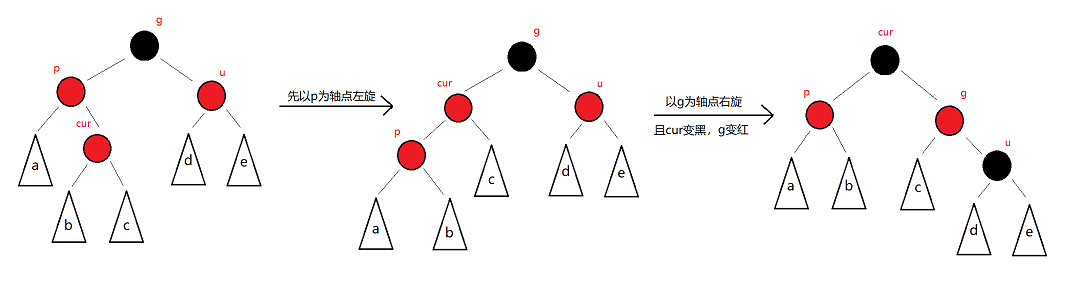
-
右左——右左双旋
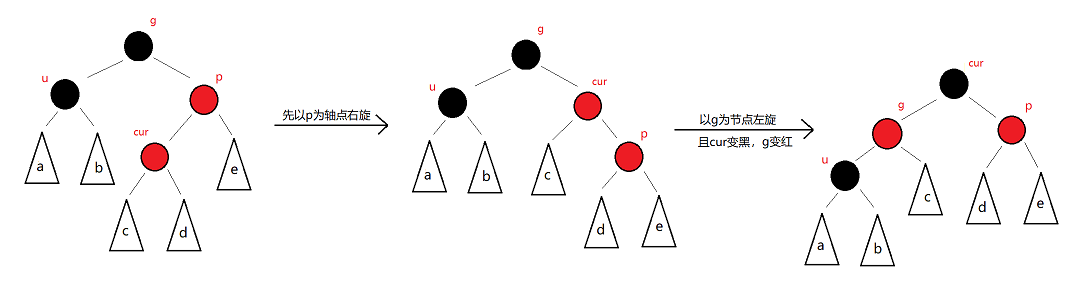
💬代码实现
template <class V>
class RBTree
{
typedef RBTreeNode<V> node;
public:
//...
bool insert(const V& v)
{
if (_root == nullptr)
{
_root = new node(v);
_root->_col = BLACK;
return true;
}
//插入
node* cur = _root;
node* parent = nullptr;
while (cur)
{
if (v < cur->_v)
{
parent = cur;
cur = cur->_left;
}
else if (v > cur->_v)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new node(v);
if (cur->_v < parent->_v)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
// 调整
node* grandfather = nullptr, *uncle = nullptr;
while (parent && parent->_col == RED) // parent存在且为红色时需继续向上调整
{
grandfather = parent->_parent;
if (parent == grandfather->_left)
{
uncle = grandfather->_right;
}
else
{
uncle = grandfather->_left;
}
//情况1:u存在且为红
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续向上更新
cur = grandfather;
parent = cur->_parent;
}
//情况2:u不存在/u存在且为黑
else
{
if (cur == parent->_left && parent == grandfather->_left)
{
// 左左——右单旋
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else if (cur == parent->_right && parent == grandfather->_right)
{
// 右右——左单旋
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else if (cur == parent->_right && parent == grandfather->_left)
{
// 左右——左右双旋
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
else if (cur == parent->_left && parent == grandfather->_right)
{
// 右左——右左双旋
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
// 经过情况2调整后,子树根节点必为黑,因此直接结束更新
break;
}
}
// 最后写定根节点为黑色
_root->_col = BLACK;
return true;
}
private:
// 右单旋
void RotateR(node* pParent)
{
node* subL = pParent->_left;
node* subLR = subL->_right;
node* ppParent = pParent->_parent;
//1.pParent(父)和subLR(子)
pParent->_left = subLR;
if (subLR)
subLR->_parent = pParent;
//2.subL(父)和pParent(子)
subL->_right = pParent;
pParent->_parent = subL;
//3.ppParent(父)和subL(子)
if (pParent == _root)
{
_root = subL;
}
else
{
if (ppParent->_left == pParent)
{
ppParent->_left = subL;
}
else
{
ppParent->_right = subL;
}
}
subL->_parent = ppParent;
}
// 左单旋
void RotateL(node* pParent)
{
node* subR = pParent->_right;
node* subRL = subR->_left;
node* ppParent = pParent->_parent;
pParent->_right = subRL;
if (subRL)
subRL->_parent = pParent;
subR->_left = pParent;
pParent->_parent = subR;
if (pParent == _root)
{
_root = subR;
}
else
{
if (ppParent->_left == pParent)
{
ppParent->_left = subR;
}
else
{
ppParent->_right = subR;
}
}
subR->_parent = ppParent;
}
node* _root;
};
5. 红黑树的验证
💭验证一棵树是否为红黑树,不能像AVL树一样简单粗暴地判断左右子树高度差的绝对值是否小于1,因为红黑树只是接近平衡。红黑树的验证需要验证其五条性质是否都成立。
⭕红黑树的性质
- 每个节点不是黑色就是红色
- 根节点为黑
- 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点
- 不允许有相邻的两个红色节点
- 每个叶节点都为黑(此处的叶节点指
NIL节点)
性质1和性质5无需验证,通过代码就已经保证了。我们需要验证性质2、3、4。
💡思路:
- 验证性质2:直接判断即可
- 验证性质3:先选取任一路径(一般旋转最左或最右路径),计算其黑节点数量,作为参考值,然后再用每一条路径的黑节点数量与参考值比较,只要有一条路径上的黑节点数量与参考值不相等,则不满足红黑树旋转3。
- 验证性质4:判断当前节点与其parent节点是否同时为红即可。(parent节点必存在,孩子节点不一定存在且情况多,所以选取parent与当前节点比较)。
💬代码实现
class RBTree
{
typedef RBTreeNode<V> node;
public:
//...
bool IsRBTree()
{
if (_root == nullptr)
{
return true;
}
// 判断性质2
if (_root->_col == RED)
{
cout << "违反性质2:根节点为黑" << endl;
return false;
}
// 求任意一条路径上的黑色节点数量,让其他路径上的与之对比
// 选取最左路径
node* left = _root;
int ref = 0;
while (left)
{
if (left->_col == BLACK)
{
ref++;
}
left = left->_left;
}
// NIL节点也是黑色
ref++;
// 检查左右子树,需要传入路径到达当前节点的黑节点的数量
return check(_root->_left, 1, ref) && check(_root->_right, 1, ref);
}
private:
bool check(node* cur, int prevBlackCount, const int& refBlackCount)
{
if (cur == nullptr)
{
// 当前路径到达终点
// 黑色节点个数与参照值比较
// 加上NIL节点
prevBlackCount++;
if (prevBlackCount != refBlackCount)
{
cout << "违反性质3:每条路径的黑节点数量应相同" << endl;
return false;
}
else
{
return true;
}
}
// 判断性质4
if (cur->_col == RED && cur->_parent->_col == RED)
{
cout << "违反性质4:不允许有相邻的两个红节点" << endl;
return false;
}
// 计算路径到达当前节点的黑节点的数量
int curBlackCount = cur->_col == BLACK ? prevBlackCount + 1 : prevBlackCount;
return check(cur->_left, curBlackCount, refBlackCount)
&& check(cur->_right, curBlackCount, refBlackCount);
}
node* _root;
};
💬 测试函数
void testRBTree()
{
RBTree<int> rbt;
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
rbt.insert(a[i]);
}
if (rbt.IsRBTree())
{
cout << "The tree is a RBTree!!!" << endl;
}
}
📃 简易的递归图
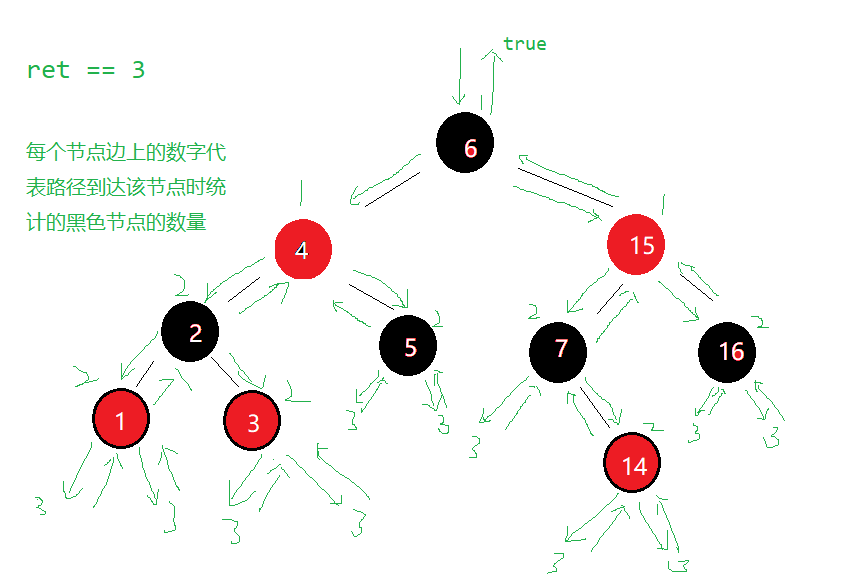
6. 红黑树和AVL树的比较
💭红黑树和AVL树都是常见的自平衡二叉搜索树,它们都能够保证树的高度不会过高,从而保证了树的查询、插入和删除操作的时间复杂度都是O(logN)。但是它们之间有一些不同点。
上面提到,红黑树是近似平衡,而AVL树是绝对平衡,因此,红黑树的查找效率低于AVL树。那么这对使用红黑树的影响大吗?那么需要探讨一下近似平衡的概念。
- 近似平衡
红黑树通过对从根到叶子节点的任一条路径上各个节点的着色方式的限制,以达到近似平衡的效果,即最长路径长度不超过最短路径的二倍。近似平衡,通俗理解,在效率方面,越接近平衡越优,越不平衡越差,若要得到其查找的时间复杂度,就要分近似平衡的最优情况和最差情况讨论。
-
最优情况:每条路径都是全黑,或者每条路径都是一红一黑相间。此时的红黑树是满二叉树,即最平衡的情况,查找的时间复杂度为
O(logN)
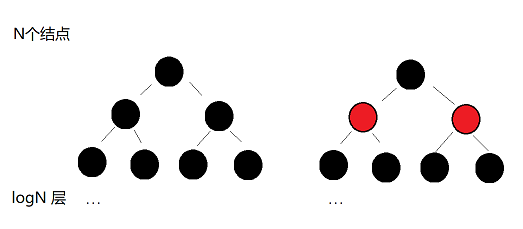
-
最差情况:每个节点的往左右的两条路径,一条全黑,一条一红一黑相间,此时左右两条路径有一条是另一条的两倍,这种情况下为最差情况。抽象示意图如下:
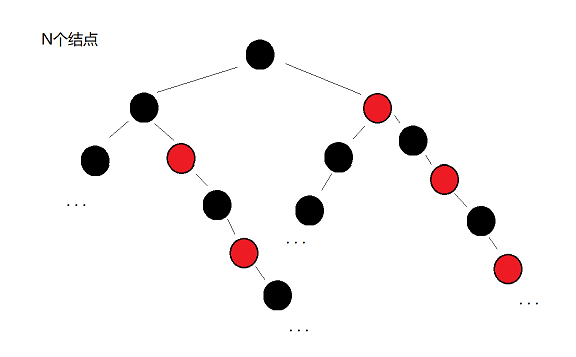
⭕分析:
设全黑路径长度(即最短路径长度):h
-
极端情况下,当N黑很大时,N红相对于N黑很小,可忽略不计
N = N黑 + N红故
N = N黑 -
此时只考虑黑色节点,可以想象成将红色节点都往最底部挪,那么上层是一个由黑色节点组成的满二叉树
故:
N黑 = N = 2^h-1h = logN
因为:全黑路径长度 = 最短路径长度 = h
所以:最长路径长度 = 2×最短路径长度 = 2h = 2logN
🔎红黑树最差情况的查找,就是去找最长路径的最后一个节点,综上推论,大概要找
2logN次。而在AVL树中,由于绝对平衡的结构,查找一个节点只需找logN次。
-
给一个很大的数,比方说10亿。那么,在一棵10亿节点的AVL树中,查找的最坏情况是找30次(log10亿)。而在一棵10亿节点的红黑树中,查找的最坏情况是找60次(2*log10亿)。可见,红黑树的查找效率略低于AVL树,但是二者是同一个量级的,对于计算机来说,这点差别不算什么。所以这点效率区别对红黑树的使用影响并不大。
-
对于树的插入和删除。AVL树在插入或删除节点时,可能会需要更多地通过旋转操作来保持树的平衡,而旋转操作可能会导致更多的旋转,从而导致插入和删除操作的时间复杂度可能会比红黑树更高。而红黑树通过着色和旋转操作来保持平衡,旋转次数比AVL树少。因此红黑树插入和删除操作的效率可能会更高。
💡得出结论:如果需要频繁进行插入和删除操作,且对查询效率要求不是特别高,可以选择红黑树;如果对查询效率有比较高的要求,且能够容忍插入和删除操作的效率稍低,可以选择AVL树。实际应用中,红黑树用的更多。
7. 红黑树的应用
- C++ STL库 – map/set、mutil_map/mutil_set
- Java 库
- linux内核
- 其他一些库
💭下一篇文章将带你了解map和set,并分析如何用红黑树实现它们。
完。