实现Newton方法的最小化函数(pytorch)

首先，我们要明确需求
def newton(theta, f, tol = 1e-8, fscale=1.0, maxit = 100, max_half = 20)
● theta是优化参数的初始值的一个向量。
● f是要最小化的目标函数。该函数应将PyTorch张量作为输入，并返回一个张量。
● tol是收敛容忍度。
● fscale 粗略估计最佳状态下f的大小–用于收敛性测试。
● maxit 在放弃之前尝试的牛顿迭代的最大数量。
● max_half 一个步骤在得出该步骤未能改善目标的结论之前应该被减半的最大次数。
目标。

1.函数需检查初始θ是否有限，并计算目标值f0。然后，使用“torch.autograd.functional”计算f在初始θ处的雅可比和hessian（同时检查它们是否是有限的）。
2.当Hessian不是正定时，使用变量“time” * 10。
3.变量“try_half”确保只输出一个关于达到最大减半次数的警告
4.更重要的是，它使用牛顿步长和方向迭代更新θ，直到达到收敛或最大迭代次数。
5.在每次迭代过程中，函数检查目标或导数在当前或新θ下是否是有限的，以及该步骤是否导向较小的目标。如果步骤未能减少目标，则函数会将步骤大小减半，直到目标减少或达到步骤减半的最大次数。如果达到步骤减半的最大次数，该功能将发出警告。
6.该函数还通过评估梯度向量的范数以及Hessian是否是正定的来检查收敛性。如果梯度向量足够接近零，函数会检查Hessian是否是正定的。如果Hessian不是正定的，函数将单位矩阵的一个小倍数（10^-8）加到Hessian上，然后重试（time*10）。
7.如果在没有收敛的情况下达到最大迭代次数，则函数会发出错误。该函数返回一个dict，其中包含theta的最终值、目标值f0、迭代次数iter_count和f在最终theta处的梯度。

def newton(theta, f, tol=1e-8, fscale=1.0, maxit=100, max_half=20): 
    # check if the initial theta is finite
    if not torch.isfinite(theta).all():
        raise ValueError("The initial theta must be finite.")
    
    # initialize variables
    iter_count = 0
    #theta is a vector of initial values for the optimization parameters
    f0 = f(theta)
    #f is the objective function to minimize， which should take PyTorch tensors as inputs and returns a Tensor
    
    #autograd functionality for the calculation of the jacobian and hessians
    grad = torch.autograd.functional.jacobian(f, theta).squeeze()
    hess = torch.autograd.functional.hessian(f, theta)
    
    # check if the objective or derivatives are not finite at the initial theta
    if not torch.isfinite(f0) or not torch.isfinite(grad).all() or not torch.isfinite(hess).all():
        raise ValueError("The objective or derivatives are not finite at the initial theta.")
    
    #multiplication factor of Hessian is positive definite 
    time = 1
    #trying max_ half step halfings
    try_half=True
    
    # iterate until convergence or maximum number of Newton iterations
    while iter_count < maxit:
        
        # calculate the Newton step and direction
        step = torch.linalg.solve(hess, grad.unsqueeze(-1)).squeeze()
        direction = -step
        
        # initialize variables for step halfing
        halfing_count = 0
        new_theta = theta + direction
        
        # iterate until the objective is reduced or max_half is reached(maximum number of times a step should be halfed before concluding that the step has failed to improve the objective)
        while halfing_count < max_half:
            
            # calculate the objective and derivatives at the new theta
            new_f = f(new_theta)
            new_grad = torch.autograd.functional.jacobian(f, new_theta).squeeze()
            new_hess = torch.autograd.functional.hessian(f, new_theta)
            
            # check if the objective or derivatives are not finite at the new theta
            if not torch.isfinite(new_f) or not torch.isfinite(new_grad).all() or not torch.isfinite(new_hess).all():
                raise ValueError("The objective or derivatives are not finite at the new theta.")
            
            # check if the step leads to a smaller objective
            if new_f < f0:
                theta = new_theta
                f0 = new_f
                grad = new_grad
                hess = new_hess
                break
                
            # if not, half the step size
            else:
                direction /= 2
                new_theta = theta + direction
                halfing_count += 1
                
        # if max_half is reached, step fails to reduce the objective, issue a warning
        if halfing_count == max_half:
            if(try_half):
                print("Warning: Max halfing count reached.")
                try_half = False
                
        # check for convergence(tol), judge whether the gradient vector is close enough to zero
        # The gradient can be judged to be close enough to zero when they are smaller than tol multiplied by the objective value
        if torch.norm(grad) < tol * (torch.abs(f0) + fscale): #add fscale to the objective value before multiplying by tol
            cholesky_hess = None
            # Check if Hessian is positive definite
            try:
                cholesky_hess = torch.linalg.cholesky(hess)
            #Hessian is not positive definite
            except RuntimeError: 
                pass
            #Hessian is still not positive definite
            if cholesky_hess is not None: 
                theta_dict = {"f": f0, "theta": theta, "iter": iter_count, "grad": grad}#return f,theta, iter, grad
                return theta_dict
            else:#If it is not positive definite, add a small multiple of the identity matrix to the Hessian and try again
                #we adding ε(the largest absolute value in your Hessian multiplied by 10^-8)
                epsilon = time * 10 ** -8 * torch.max(torch.abs(hess)).item() 
                hess += torch.eye(hess.shape[0], dtype=hess.dtype) * epsilon
                # keep multiplying ε by 10 until Hessian is positive definite
                time *= 10
                
                
        # update variables for the next iteration
        iter_count += 1
    
    # if maxit is reached without convergence, issue an error
    raise RuntimeError("Max iterations reached without convergence.")

测试案例

对于以上newton()函数，采用以下五个函数测试找到全局最小值验证有效性（使用3个不同的起始值（theta））
$$f(x,y)=x^2-2x+2y^2+y+3$$

$$f(x,y)=100\ast (y-x^2{)}^2+(1-x{)}^2$$

$$f(x_1,\dots ,x_5)=\sum _{i=1}^4\left[100(x_{i+1}-x_i^2{)}^2+(1-x_i{)}^2\right]$$

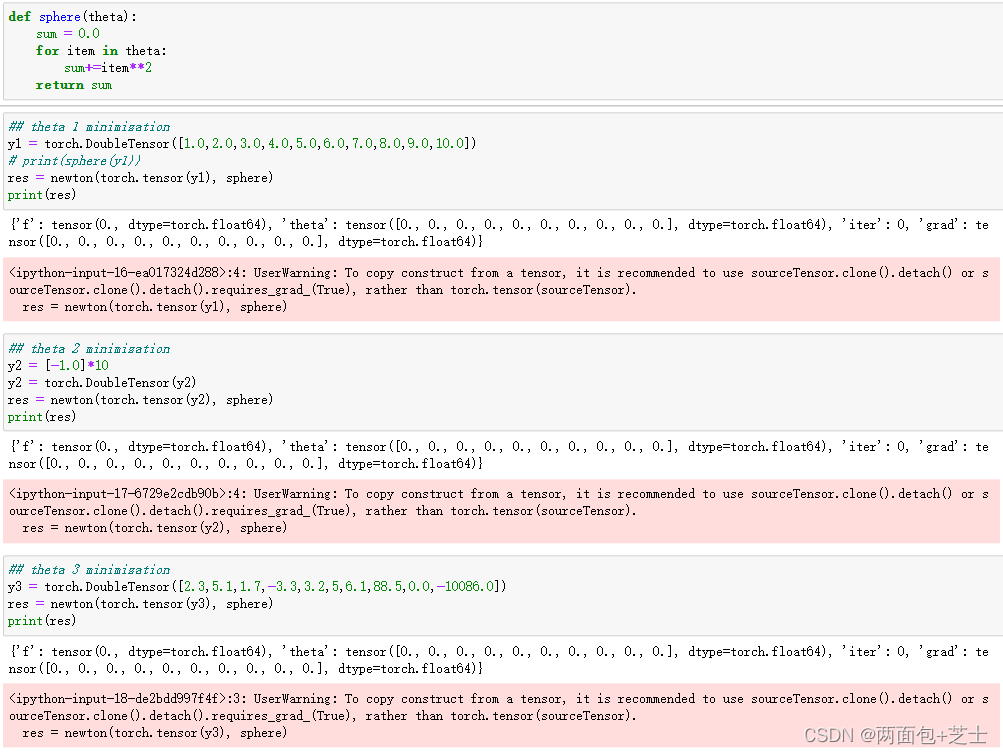
$$f(x_1,\dots ,x_{1}0)=\sum _{i=1}^{10}{x}_i^2$$

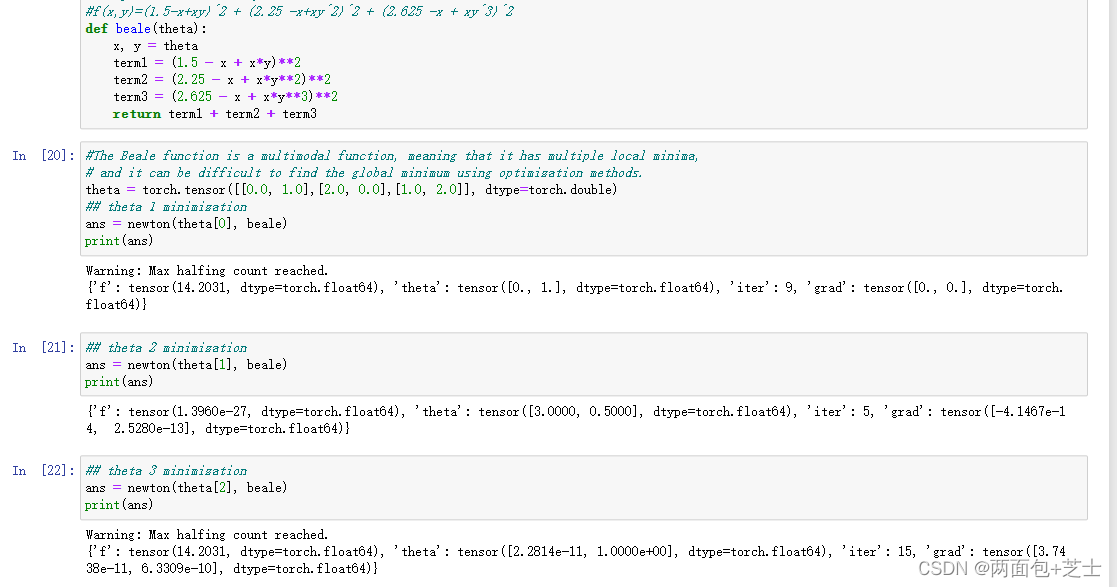
$$f(x,y)=(1.5-x+xy{)}^2+(2.25-x+x{y}^2{)}^2+(2.625-x+x{y}^3{)}^2$$