PyTorch 矩阵乘法总结和运算符重载
1. 二维矩阵乘法 torch.mm()
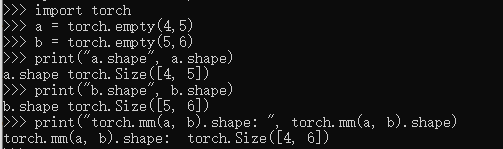
也就是最基本的矩阵乘法,需要满足对应维度的要求,否则报错
torch.mm(mat1, mat2, out=None)
mat1
∈
R
m
×
n
\in \mathbb{R}^{m \times n}
∈Rm×n,mat2
∈
R
n
×
d
\in \mathbb{R}^{n \times d}
∈Rn×d,输出 out
∈
R
m
×
d
\in \mathbb{R}^{m \times d}
∈Rm×d。
2. 三维带batch的矩阵乘法 torch.bmm()
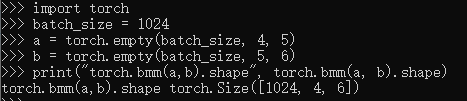
torch.bmm(bmat1, bmat2, out=None)
由于神经网络训练一般采用 mini-batch,经常输入的是三维带 batch 的矩阵。
提供 torch.bmm(bmat1, bmat2, out=None),
其中 bmat1 ∈ R b a t c h × m × n \in \mathbb{R}^{batch \times m \times n} ∈Rbatch×m×n,bmat2 ∈ R b a t c h × n × d \in \mathbb{R}^{batch \times n \times d} ∈Rbatch×n×d,out ∈ R b a t c h × m × d \in \mathbb{R}^{batch \times m \times d} ∈Rbatch×m×d。
3. 多维矩阵乘法 torch.matmul()
torch.matmul(input, other, out=None)
支持broadcast操作,使用起来比较复杂。
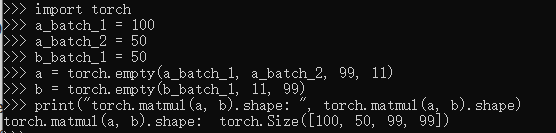
针对多维数据 matmul()乘法,我们可以认为该matmul()乘法使用使用两个参数的后两个维度来计算,其他的维度都可以认为是batch维度。
假设两个输入的维度分别是
input ∈ R 1000 × 500 × 99 × 11 \in \mathbb{R}^{1000 \times 500 \times 99 \times 11} ∈R1000×500×99×11, other ∈ R 500 × 11 × 99 \in \mathbb{R}^{500 \times 11\times 99} ∈R500×11×99
可以认为 torch.matmul(input, other, out=None) 乘法首先是进行后两位矩阵乘法得到(99×11)×(11×99)⇒(99×99),然后分析两个参数的batch size分别是 (1000×500) 和 500 。
可以广播成为 (1000×500), 因此最终输出的维度是 (1000×500×99×99)。
4. 矩阵逐元素(Element-wise)乘法 torch.mul()
torch.mul(mat1, other, out=None)
其中 other 乘数可以是标量,也可以是任意维度的矩阵,只要满足最终相乘是可以 broadcast 的即可

5. 运算符重载
import torch
import numpy as np
a = torch.rand(2,3)
b = torch.rand(3)
# 这里b 使用了 broatcasting 自动进行了维度扩展
print("运算符 + 与 add() 方法运算结果一致:{} ".format(torch.all(torch.eq(torch.add(a,b),a+b))))
print("运算符 - 与 sub() 方法运算结果一致:{} ".format(torch.all(torch.eq(torch.sub(a,b),a-b))))
print("运算符 * 与 mul() 方法运算结果一致:{} ".format(torch.all(torch.eq(torch.mul(a,b),a*b))))
print("运算符 / 与 div() 方法运算结果一致:{} ".format(torch.all(torch.eq(torch.div(a,b),a/b))))
运算符 + 与 add() 方法运算结果一致:True
运算符 - 与 sub() 方法运算结果一致:True
运算符 * 与 mul() 方法运算结果一致:True
运算符 / 与 div() 方法运算结果一致:True
矩阵相乘 torch.matmul(只取最后两维度进行运算), @(是matmul方法的重载) 两种方法
import torch
import numpy as np
a = torch.rand(2,3)
b = torch.rand(3,4)
print("运算符 @ 与 matmul 方法运算结果一致:{} ".format(torch.all(torch.eq(torch.matmul(a,b),a@b))))
print("运算后张量的 shape: {}".format((a@b).shape))
运算符 @ 与 matmul 方法运算结果一致:True
运算后张量的 shape: torch.Size([2, 4])
pow / ** 幂运算
import torch
import numpy as np
a = torch.full([2,2],2)
print("a 的二次方: {}".format(a.pow(2)))
print("a 的三次方: {}".format(a**3))
#平方根
print("a 的平方根: {}".format(torch.sqrt(a.pow(2))))
a 的二次方: tensor([[4., 4.],
[4., 4.]])
a 的三次方: tensor([[8., 8.],
[8., 8.]])
a 的平方根: tensor([[2., 2.],
[2., 2.]])
exp / log
import torch
import numpy as np
a = torch.exp(torch.ones(2,2))
print("e 为: {}".format(a))
print("e 取log : {}".format(torch.log(a)))
e 为: tensor([[2.7183, 2.7183],
[2.7183, 2.7183]])
e 取log : tensor([[1., 1.],
[1., 1.]])
clamp 范围限幅
(min)将低于min的值裁剪为min
(min,max) 将数据低于min 裁剪为min,高于max裁剪为max
import torch
import numpy as np
a = torch.randn(2,3)
print("a 为: {}".format(a))
print("a 裁剪后为 : {}".format(a.clamp(0.1)))
print("a 裁剪后为 : {}".format(a.clamp(0.1,0.3)))
a 为: tensor([[-0.4780, -0.2077, 0.3702],
[-1.5801, -0.0170, 0.6737]])
a 裁剪后为 : tensor([[0.1000, 0.1000, 0.3702],
[0.1000, 0.1000, 0.6737]])
a 裁剪后为 : tensor([[0.1000, 0.1000, 0.3000],
[0.1000, 0.1000, 0.3000]])