总结下研一小白入门pytorch时遇到的基础问题（只求自己能看懂篇）

1.numpy到底是什么？

numpy是python中的一个库，主要用于矩阵和数组的运算。

2.pytorch深度学习框架那么深度学习框架是什么意思？

在其他文章里看到一个很好的解释，对我这种理解力低下的小白很友好。深度学习框架好比是一套积木，每一块小积木就是其中的一个库or包，你想怎么搭建这个积木都可以，总之这套积木里有你需要的所有小积木。

3.张量（tensor）是什么？

这是个困扰我很久并且继续困扰下去的问题。张量就是，在不同参考系下按照某种特定法则进行变换的量。这句话我到现在还是一知半解，关于什么是张量，我已经看到了许多个版本的解释，因为我参不透本质，所以每个版本说的都不一样。但是在知乎上看到一篇帖子解释张量还是比较容易懂的，帖子中大体意思是说：用物理学观点来解释张量，比如Bob认为粒子的能动量是（Ea，Pa），而Andy则认为是（Eb，Pb），Bob和Andy都没有说错，因为（Ea，Pa）和（Eb，Pb）是可以通过一定条件相互转换的，二者只是参考系的不同，Andy和Bob各自的参考系并没有哪一个更优越一说，于是我们干脆都舍弃，这个粒子的能动量就由张量T来表示，所以物理学定义就出来了，张量是一个不随坐标而改变的，物理系统内在的量。而在数学家眼里，张量就类似于线性变换，不依赖与线性空间中基的选取。不管是物理还是数学，张量都是可根据参考系而发生相应变换的量。

4.有关GPU

（1）NVIDIA是什么

NVIDIA，中文名叫英伟达（在很多笔记本电脑的标签上经常可以看到），英伟达是一家人工智能公司，说白了就是一家能生产显卡的厂商，英伟达发明了GPU，彻底改变了并行计算，由此可见，GPU是可以加快程序效率并可以实现并行计算处理的。

（2）CUDA是什么

cuda是显卡厂商NVIDIA推出的运算平台。是一种通用并行计算得架构，可以使GPU能够解决复杂的计算问题。目前cuda只支持linux和win系统，进行cuda开发需要一次安装驱动、toolkit、SDK三个软件，安装cuda是为了使用GPU加速。

（3）GPU

显卡的处理器称为图形处理器（Graphics Processing Unit，GPU）。gpu是专为执行复杂的数学和几何计算而设计的。

5.各种代码细节问题

①/和// :/表示除法；//表示向下取整的除法

②带lib后缀的代码是指library库

③代码中dim的含义，dim即dimension，是指维度，有关dim，我找到一个博主写的非常容易理解且详细，附上链接Python-维度dim的定义及其理解使用_静静喜欢大白的博客-CSDN博客_python中dim

为了保存文字我再复制一遍：

一、dim的定义

TensorFlow对张量的阶、维度、形状有着明确的定义，而在pytorh中对其的定义却模糊不清，仅仅有一个torch.size()的函数来查看张量的大小（我理解的这个大小指的就是TensorFlow对张量的形状描述，也和numpy的.shape类似）。所以，首先要搞清楚如何看一个张量的形状。

import torch
z = torch.ones(2,3,4)
print(z)
print(z.size())
print(z.size(0))
print(z.size(1))
print(z.size(2))

以上代码的控制台输出为：

tensor([[[1., 1., 1., 1.],

[1., 1., 1., 1.],

[1., 1., 1., 1.]],

[[1., 1., 1., 1.],

[1., 1., 1., 1.],

[1., 1., 1., 1.]]])

torch.Size([2, 3, 4])

2

3

4

可见，我们成功创建了一个（2，3，4）大小的张量，那么我们人工应该怎么辨别一个张量的大小呢？为了直观，我把这个张量的中括号调整一个位置：

[

[

[1., 1., 1., 1.],

[1., 1., 1., 1.],

[1., 1., 1., 1.]

],

[

[1., 1., 1., 1.],

[1., 1., 1., 1.],

[1., 1., 1., 1.]

]

]

我们可以看到：

第一层（最外层）中括号里面包含了两个中括号（以逗号进行分割），这就是（2，3，4）中的2
第二层中括号里面包含了三个中括号（以逗号进行分割），这就是（2，3，4）中的3
第三层中括号里面包含了四个数（以逗号进行分割），这就是（2，3，4）中的4

结论：pytorch中的tensor维度可以通过第一个数前面的中括号数量来判断，有几个中括号维度就是多少。拿到一个维度很高的向量，将最外层的中括号去掉，数最外层逗号的个数，逗号个数加一就是最高维度的维数，如此循环，直到全部解析完毕。

我们还看到：

z.size(0) = 2，z.size(1) = 3，z.size(2) = 4

第0维度为2，第1维度为3，第2维度为4，即维度的标号是以0开始的。

dim = 0，列不变（按列-将当前列所有行数据-计算），指定的是行，那就是行变，理解成：针对每一列中，所有行之间的数据比较或者求和等操作，是每一行的比较，因为行是可变的。
dim = 1，行不变（按行-将当前行所有列数据-计算），指定的是列，那就是列变，理解成：针对每一行中，所有列之间的数据比较或者求和等操作，是每一行的比较，因为行是可变的。

原博客还有图解，在此不做copy。

对于dim分别等于0,1，-1，2的情况，另一位博主写的可能略有不同：

原贴链接附上：pytorch中tf.nn.functional.softmax(x,dim = -1)对参数dim的理解_Will_Ye的博客-CSDN博客_dim

在此复制一遍：

一般会有设置成dim=0,1,2,-1的情况

准备工作：先随机生成一个（2,2,3）的矩阵，两个维度的（2,3）矩阵。

import torch
import torch.nn.functional as F
input = torch.randn(2,2,3))
print(input)

    1
    2
    3
    4

输出为：

tensor([[[-3.9332,  0.7909,  0.8927],
         [-1.7991,  0.2505,  0.7695]],

        [[ 0.1946,  0.1878,  1.2713],
         [ 0.9536,  1.0525, -0.7081]]])

    1
    2
    3
    4
    5

要注意的是当dim=0时，是对每一维度相同位置的数值进行softmax运算，举个栗子：

m = F.softmax(input,dim=0)
print(m)

    1
    2

输出为：

tensor([[[0.0159, 0.6464, 0.4065],
         [0.0599, 0.3096, 0.8142]],

        [[0.9841, 0.3536, 0.5935],
         [0.9401, 0.6904, 0.1858]]])

    1
    2
    3
    4
    5

从输出结果可以看出，一共2个维度
每一个维度（2,3）对应的数值相加为1，例如：

[0][0][0]+[1][0][0]=0.0159+0.9841=1
[0][0][1]+[1][0][1]=0.6464+0.3536=1

要注意的是当dim=1时，是对某一维度的列进行softmax运算：

m = F.softmax(input,dim=1)
print(m)

    1
    2

输出为：

tensor([[[0.1058, 0.6319, 0.5308],
         [0.8942, 0.3681, 0.4692]],

        [[0.3189, 0.2964, 0.8786],
         [0.6811, 0.7036, 0.1214]]])

    1
    2
    3
    4
    5

从输出结果可以看出，计算的是某一维度中的列，例如：
在第1维度中：
[0][0][0]+[0][1][0]=0.1058+0.8942=1
在第2维度中：
[1][0][0]+[1][1][0]=0.3189+0.6811=1

要注意的是当dim=2时，是对某一维度的行进行softmax运算：

m = F.softmax(input,dim=2)
print(m)

    1
    2

输出为：

tensor([[[0.0042, 0.4726, 0.5232],
         [0.0458, 0.3560, 0.5982]],

        [[0.2029, 0.2015, 0.5955],
         [0.4360, 0.4813, 0.0828]]])

    1
    2
    3
    4
    5
    6

从输出结果可以看出，计算的是某一维度中的行，例如：
在第1维度中：
[0][0][0]+[0][0][1]+[0][0][2]=0.0042+0.4726+0.5232=1
在第2维度中：
[1][0][0]+[1][0][1]+[1][0][2]=0.2029+0.2015+0.5955=0.9999=1（是等于1的，只是后面还有很多位小数省略了）

要注意的是当dim=-1时，是对某一维度的行进行softmax运算：

m = F.softmax(input,dim=-1)
print(m)

    1
    2

输出为：

tensor([[[0.0042, 0.4726, 0.5232],
         [0.0458, 0.3560, 0.5982]],

        [[0.2029, 0.2015, 0.5955],
         [0.4360, 0.4813, 0.0828]]])

    1
    2
    3
    4
    5

从这里可以发现，dim=-1和dim=2的结果是一样的。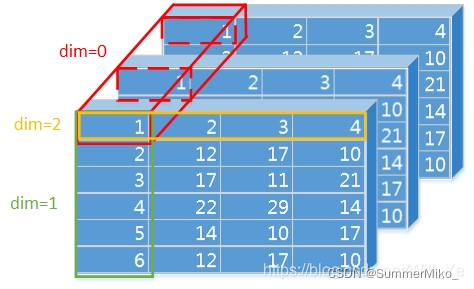

我个人采用了第二位博主的理解方式。关于维度可以用一句话总结，0表示张量的最高维度，1表示张张量的次高维度，2表示张量的次次高维度，以此类推。-1表示张量维度的最低维度，-2表示倒数第二维度，-3表示倒数第三维度。文中，张量就三个维度，所以dim=-1和dim=2的相同