二维图形是将平面坐标上的数据点连接起来的平面图形。可以采用不同的坐标系,除直角坐标系外,还可以采用对数坐标、极坐标。数据点可以用向量或矩阵形式给出,类型可以是实型或复型。二维曲形的绘制无疑是其他绘图操作的基础。 在 MATLAB 中,基本的绘图函数是 plot 函数,利用它可以绘制出不同的二维曲线。 plot 函数用于绘制
x
y
xy
x y
x
x
x
y
y
y
x
x
x
y
y
y plot 函数的基本调用格式如下: plot ( x, y)
其中,
x
x
x
y
y
y
x
x
x
y
y
y 例如,在
0
≤
x
≤
2
π
0\le x\le2\pi
0 ≤ x ≤ 2 π
y
=
2
e
−
0.5
x
sin
(
2
π
x
)
y=2e^{-0.5x}\sin(2\pi x)
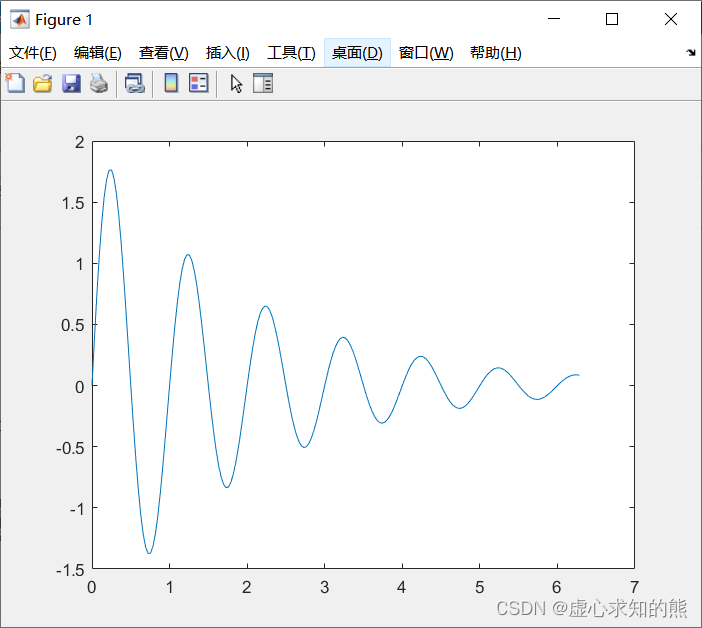
y = 2 e − 0.5 x sin ( 2 π x ) 程序如下: x= 0 : pi/ 100 : 2 * pi;
y= 2 * exp ( - 0.5 * x) . * sin ( 2 * pi* x) ;
plot ( x, y)
程序运行后,打开一个图像窗口,在其中绘制函数曲线。
这里需要注意的是,求
y
y
y
x
x
x
y
y
y
y
(
i
)
y(i)
y ( i )
x
(
i
)
x(i)
x ( i ) 例如,我们绘制曲线:
{
x
=
t
cos
3
t
y
=
t
sin
2
t
−
π
≤
t
≤
π
\left\{\begin{matrix}x=t\cos 3t \\y=t\sin^{2} t \end{matrix}\right. \begin{matrix} -\pi \le t\le \pi \end{matrix}
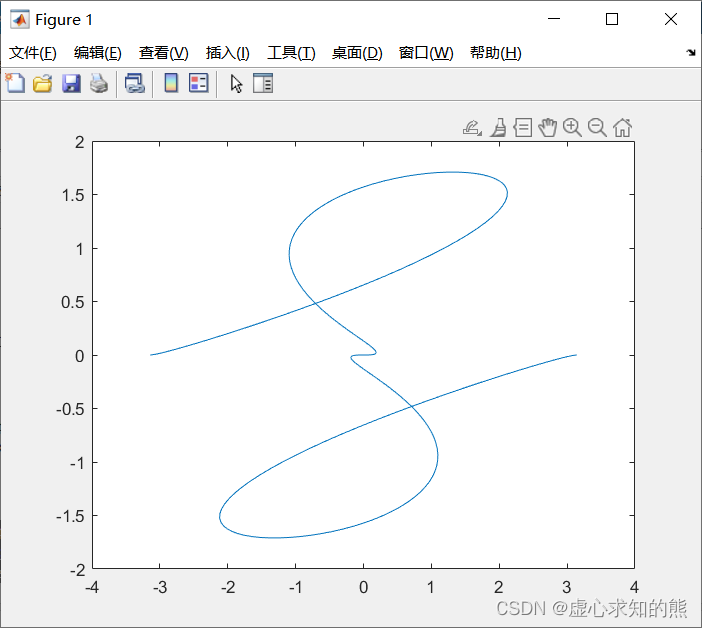
{ x = t cos 3 t y = t sin 2 t − π ≤ t ≤ π 这是以参数方程形式给出的二维曲线,只要给定参数向量,再分别求出
x
、
y
x、y
x 、 y t= - pi: pi/ 100 : pi;
x= t. * cos ( 3 * t) ;
y= t. * sin ( t) . * sin ( t) ;
plot ( x, y)
以上提高 plot 函数的自变量
x
、
y
x、y
x 、 y (1) 当
x
x
x
y
y
y
x
x
x
y
y
y 如果
x
x
x
y
y
y
x
x
x
y
y
y
y
y
y 如果
x
x
x
y
y
y
x
x
x
y
y
y
y
y
y 如果
y
y
y
x
x
x
y
y
y
x
x
x
y
y
y x= linspace ( 0 , 2 * pi, 100 ) ;
y= [ sin ( x) , cos ( x) ] ;
plot ( x, y)
程序首先产生一个行向量
x
x
x
x
x
x
x
x
x
y
y
y 当
x
x
x
y
y
y
x
x
x (2) 当
x
、
y
x、y
x 、 y
x
、
y
x、y
x 、 y t= linspace ( 0 , 2 * pi, 100 ) ;
x= [ t; t] ';
y= [ sin ( t) ; cos ( t) ] ';
plot ( x, y)
(3) plot 函数最简单的调用格式是只包含一个输入参数,即 plot(x)。 在这种情况下,当
x
x
x 当
x
x
x t= 0 : 0.01 : 2 * pi;
x= exp ( i* t) ; % x是一个复数向量
plot ( x)
这里需要注意的是,程序中的 i 是虚数单位,这样
x
x
x 当
x
x
x
x
x
x t= 0 : 0.01 : 2 * pi;
x= exp ( i* t) ;
y= [ x; 2 * x; 3 * x] ';
plot ( y)
plot 函数可以包含若干组向量对,每一向量对可以绘制出一条曲线。相应的调用格式如下:plot ( x1, y1, x2, y2, . . . , xn, yn)
(1) 当输入参数都为向量时,
x
1
x1
x 1
y
1
,
x
2
y1,x2
y 1 , x 2
y
2
,
…
,
x
n
y2,…,xn
y 2 , … , x n
y
n
yn
y n x= linspace ( 0 , 2 * pi, 100 ) ;
plot ( x, sin ( x) , x, 2 * sin ( x) , x, 3 * sin ( x) )
(2) 当输入参数有矩阵形式时,配对的
x
、
y
x、y
x 、 y x= linspace ( 0 , 2 * pi, 100 ) ;
y1= sin ( x) ;
y2= 2 * sin ( x) ;
y3= 3 * sin ( x) ;
x= [ x; x; x] ';
y= [ y1; y2; y3] ';
plot ( x, y, x, cos ( x) )
x
x
x
y
y
y
x
x
x
x
x
x MATLAB 提供了一些绘图选项, 用于确定所绘曲线的线型、颜色和数据点标记符号。这些选项可以组合使用。例如,b- . 表示蓝色点画线,y:d 表示黄色虚线并用菱形符标记数据点。 当选项省略时,MATLAB 规定,线型一律用实线,自动循环使用当前坐标轴的 ColorOrder 属性指定的颜色(默认有 7 种颜色),无数据点标记符号。 线型选项如下表所示。 选项 线型 选项 线型 - 实现(默认值) -. 点画线 : 虚线 – 双画线
序号 选项 颜色 序号 选项 颜色 1 b(blue) 蓝色 5 m(magenta) 品红色 2 g(green) 绿色 6 y(yellow) 黄色 3 r(red) 红色 7 k(black) 黑色 4 c(cyan) 青色 8 w(white) 白色
选项 标记符号 选项 标记符号 . 点 v(字母) 朝下三角符号 o(字母) 圆圈 ^ 朝上三角符号 x(字母) 叉号 < 朝左三角符号 + 加号 > 朝右三角符号 * 星号 p(pentagram) 五角星符 s(square) 方块符 h(hexagram) 六角星符 d(diamond) 菱形符
要设置曲线样式可以在 plot 函数中加绘图选项,其调用格式如下: plot ( x1, y1, 选项1 , x2, y2, 选项2 , . . . , xn, yn, 选项n)
例如,用不同线刑和颜色在同一坐标内绘制曲线
y
=
2
e
−
0.5
x
sin
(
2
π
x
)
y=2e^{-0.5x}\sin(2\pi x)
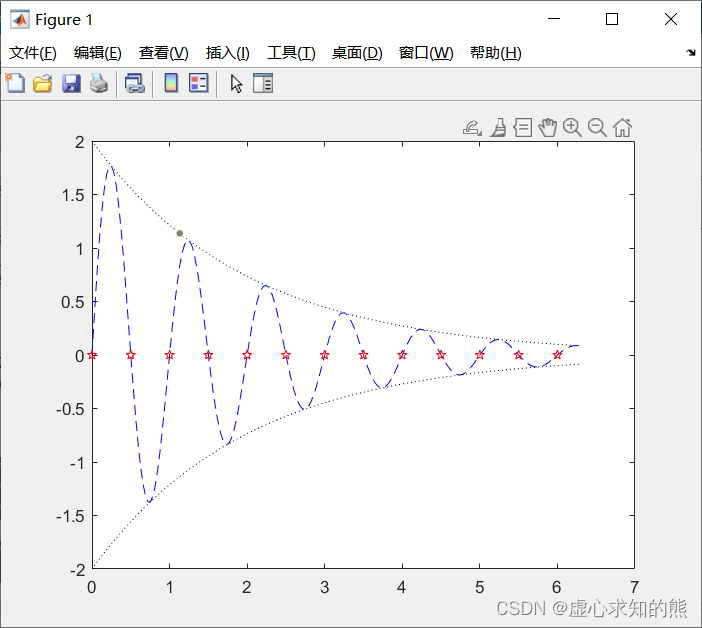
y = 2 e − 0.5 x sin ( 2 π x ) 程序如下: x= ( 0 : pi/ 100 : 2 * pi) ';
y1= 2 * exp ( - 0.5 * x) * [ 1 , - 1 ] ;
y2= 2 * exp ( - 0.5 * x) . * sin ( 2 * pi* x) ;
x1= ( 0 : 12 ) / 2 ;
y3= 2 * exp ( - 0.5 * x1) . * sin ( 2 * pi* x1) ;
plot ( x, y1, 'k:' , x, y2, 'b--' , x1, y3, 'rp' ) ;
程序运行结果如下所示。plot 函数中包含 3 组绘图参数,第一组用黑色虚线绘出两根包络线,第二组用蓝色双画线绘出曲线
y
y
y
在MATLAB中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy函数, plotyy ( x1, y1, x2, y2)
其中,
x
1
,
y
1
x1,y1
x 1 , y 1
x
2
,
y
2
x2,y2
x 2 , y 2
x
1
,
y
1
x1,y1
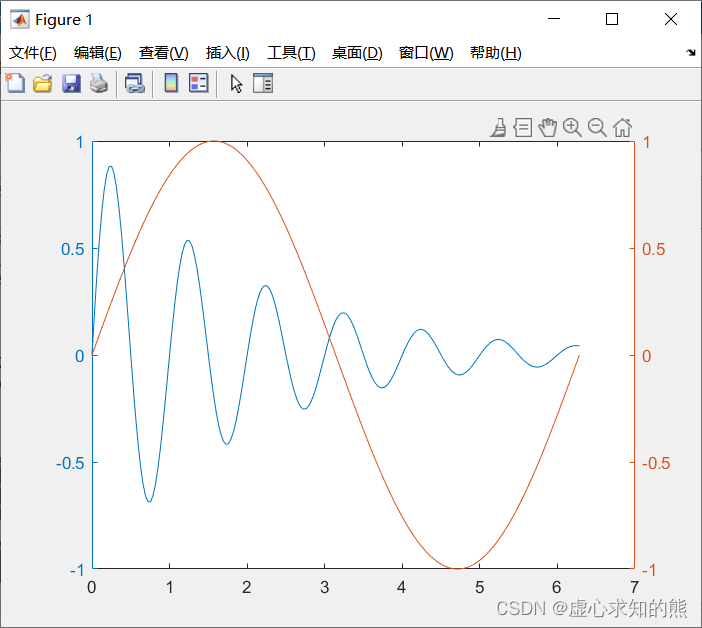
x 1 , y 1 双纵坐标图形能把函数值具有不同量纲、不同数量级的两个函数绘制在同-一坐标中,有利于图形数据的对比分析。 例如,用不同标度在同一坐标内绘制曲线
y
=
2
e
−
0.5
x
sin
(
2
π
x
)
y=2e^{-0.5x}\sin(2\pi x)
y = 2 e − 0.5 x sin ( 2 π x )
y
=
s
i
n
x
y=sinx
y = s in x 程序如下: x= 0 : pi/ 100 : 2 * pi;
y1= exp ( - 0.5 * x) . * sin ( 2 * pi* x) ;
y2= sin ( x) ;
plotyy ( x, y1, x, y2) ;
绘制完图形后,可能还需要对图形进行一些辅助操作,以使图形意义更加明确,可读性更强。 在绘制图形的同时,可以对图形加上一些说明,如图形名称、坐标轴说明以及图形某一部分的含义等,这些操作称为添加图形标注。有关图形标注函数的调用格式如下: title ( 图形名称)
xlabel ( x轴说明)
ylabel ( y轴说明)
text ( x, y, 图形说明)
legend ( 图例1 , 图例2 , …)
title 和 xlabel、ylabel 函数分别用于说明图形和坐标轴的名称。text 函数是在 (x, y) 坐标处添加图形说明。gtext 可以用来添加文本说明,执行该命令时,十字坐标光标自动跟随鼠标移动,单击鼠标即可将文本放置在十字光标处。例如,使用 gtext('cos(x)) 可放置字符串 cos(x)。legend 函数用于绘制曲线所用线型、颜色或数据点标记图例,图例放置在图形空白处,用户还可以通,过鼠标移动图例,将其放到所希望的位置。除 legend 函数外,其他函数同样适用于三维图形,需要注意的是,z 坐标轴说明用 zlabel 函数。 上述函数中的说明文字,除使用标准的 ASCII 字符外,还可以使用 LaTeX(LaTeX 是一种十分流行的数学排版软件)格式的控制字符,这样就可以在图形上添加希腊字母、数学符号及公式等内容。 在 MATLAB 支持的 LaTeX 字符中,用 \bf、 \it、\rm 控制字符分别定义黑体、斜体和正体字符,受 LaTeX 字符控制部分要加大括号 {} 括起来。例如,text(0.3,0.5,‘The useful {\bf MATLAB}’) 将使得 MATLAB 一词黑体显示。 一些常用的 LaTeX 字符如下表所示,其中的各个字符既可以单独使用,又可以和其他字符及命令联合使用。例如,text(1,1,'sin({\omega}t+ {beta})) 将得到标注效果 sin(
ω
\omega
ω
β
\beta
β 标识符 符号 标识符 符号 标识符 符号 \alpha
α
\alpha
α \upsilon
υ
\upsilon
υ \sim
∼
\sim
∼ \beta
β
\beta
β \phi
ϕ
\phi
ϕ \leq
≤
\leq
≤ \gamma
γ
\gamma
γ \chi
χ
\chi
χ \infty
∞
\infty
∞ \delta
δ
\delta
δ \psi
ψ
\psi
ψ \clubsuit
♣
\clubsuit
♣ \epsilon
ϵ
\epsilon
ϵ \omega
ω
\omega
ω \diamondsuit
♢
\diamondsuit
♢ \zeta
ζ
\zeta
ζ \Gamma
Γ
\Gamma
Γ \heartsuit
♡
\heartsuit
♡ \eta
η
\eta
η \Delta
Δ
\Delta
Δ \spadesuit
♠
\spadesuit
♠ \theta
θ
\theta
θ \Theta
Θ
\Theta
Θ \leftrightarrow
↔
\leftrightarrow
↔ \vartheta
ϑ
\vartheta
ϑ \Lambda
Λ
\Lambda
Λ \leftarrow
←
\leftarrow
← \iota
ι
\iota
ι \Xi
Ξ
\Xi
Ξ \uparrow
↑
\uparrow
↑ \kappa
κ
\kappa
κ \Pi
Π
\Pi
Π \rightarrow
→
\rightarrow
→ \lambda
λ
\lambda
λ \Sigma
Σ
\Sigma
Σ \downarrow
↓
\downarrow
↓ \mu
μ
\mu
μ \Upsilon
Υ
\Upsilon
Υ \circ
∘
\circ
∘ \nu
ν
\nu
ν \Phi
Φ
\Phi
Φ \pm
±
\pm
± \xi
ξ
\xi
ξ \Psi
Ψ
\Psi
Ψ \geq
≥
\geq
≥ \pi
π
\pi
π \Omega
Ω
\Omega
Ω \propto
∝
\propto
∝ \rho
ρ
\rho
ρ \forall
∀
\forall
∀ \partial
∂
\partial
∂ \sigma
σ
\sigma
σ \exists
∃
\exists
∃ \bullet
∙
\bullet
∙ \varsigma
ς
\varsigma
ς \ni
∋
\ni
∋ \div
÷
\div
÷ \tau
τ
\tau
τ \cong
≅
\cong
≅ \neq
≠
\neq
= \equiv
≡
\equiv
≡ \approx
≈
\approx
≈ \aleph
ℵ
\aleph
ℵ \Im
ℑ
\Im
ℑ \Re
ℜ
\Re
ℜ \wp
℘
\wp
℘ \otimes
⊗
\otimes
⊗ \oplus
⊕
\oplus
⊕ \oslash
⊘
\oslash
⊘ \cap
∩
\cap
∩ \cup
∪
\cup
∪ \supseteq
⊇
\supseteq
⊇ \supset
⊃
\supset
⊃ \subseteq
⊆
\subseteq
⊆ \subset
⊂
\subset
⊂ \int
∫
\int
∫ \in
∈
\in
∈ \nabla
∇
\nabla
∇ \rfloor
⌋
\rfloor
⌋ \lceil
⌈
\lceil
⌈ \ldots
…
\ldots
… \lfloor
⌊
\lfloor
⌊ \cdot
⋅
\cdot
⋅ \prime
′
\prime
′ \perp
⊥
\perp
⊥ \neg
¬
\neg
¬ \mid
∣
\mid
∣ \wedge
∧
\wedge
∧ \times
×
\times
× \copyright
©
\copyright
c ◯ \rceil
⌉
\rceil
⌉ \surd
√
\surd
√ \varpi
ϖ
\varpi
ϖ \vee
∨
\vee
∨ \langle
⟨
\langle
⟨ \rangle
⟩
\rangle
⟩
除了上表中给出的字符定义以外,还可以通过标准的 LaTeX 命令来定义上标和下标,这样可以使得图形标注更加丰富多彩。如果想在某个字符后面添加上标,则可以在该字符后面跟一个由 A 字符引导的字符串。 若想把多个字符作为指数,则应该使用大括号。例如,e^{axt} 对应的标注效果为
e
a
x
t
e^{axt}
e a x t
e
a
x
t
e^{a}xt
e a x t
X
12
X_{12}
X 12 在绘制图形时,MATLAB 可以自动根据要绘制曲线数据的范围选择合适的坐标刻度,使得曲线能够尽可能清晰地显示出来。所以,在一般情况下用户不必选择坐标轴的刻度范围。但是,如果用户对坐标系不满意,可利用 axis 函数对其重新设定。该函数的调用格式如下: axis ( [ xmin, xmax, ymin, ymax, zmin, zmax] )
如果只给出前 4 个参数,则 MATLAB 按照给出的
x
、
y
x、y
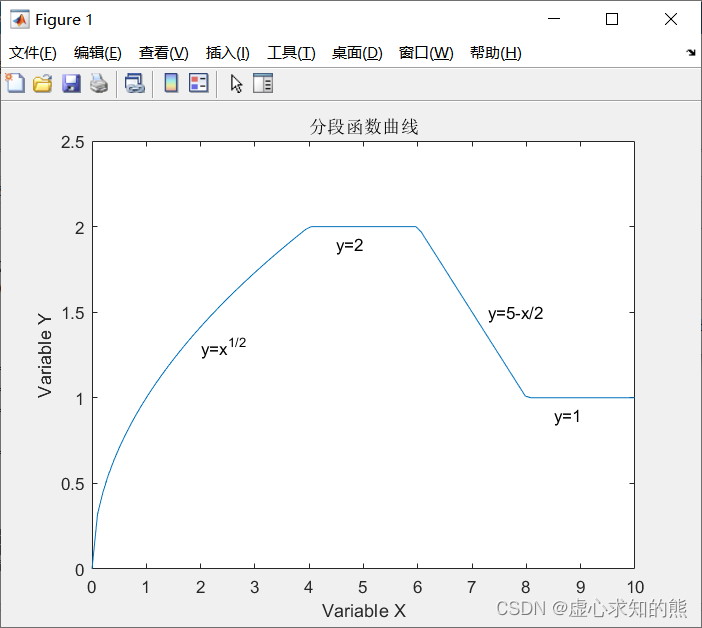
x 、 y 如果给出了全部参数,则系统按照给出的 3 个坐标轴的最小值和最大值选择坐标系范围,以便绘制出合适的三维图形。 axis 函数功能丰富,常用的用法还有以下几种。(1) axis equal 表示纵、横坐标轴采用等长刻度。 (2) axis square 表示产生正方形坐标系(默认为矩形)。 (3) axis auto 表示使用默认设置。 (4) axis off 表示取消坐标轴。 (5) axis on 表示显示坐标轴。 给坐标加网格线可以用 grid 命令来控制。grid on/off 命令控制是画还是不画网格线,不带参数的 grid 命令在两种状态之间进行切换。 给坐标加边框用 box 命令来控制。box on/off 命令控制是加还是不加边框线,不带参数的 box 命令在两种状态之间进行切换。 例如,我们绘制分段函数曲线并添加图形标注。
f
(
x
)
=
{
x
,
2
,
5
−
x
/
2
,
1
,
0
≤
x
<
4
4
≤
x
<
6
6
≤
x
<
8
x
≥
8
f(x)=\left\{\begin{matrix}\sqrt{x} , \\2, \\5-x/2, \\1,\end{matrix}\right. \begin{matrix}0\le x< 4 \\4\le x< 6 \\6\le x< 8 \\x\ge 8 \end{matrix}
f ( x ) = ⎩
⎨
⎧ x
, 2 , 5 − x /2 , 1 , 0 ≤ x < 4 4 ≤ x < 6 6 ≤ x < 8 x ≥ 8 整体程序如下: x= linspace ( 0 , 10 , 100 ) ; % 产生自变量向量x
y= [ ] ; % y的初始值为空
for x0= x
if x0>= 8
y= [ y, 1 ] ; % 将函数值追加到向量y
elseif x0>= 6
y= [ y, 5 - x0/ 2 ] ;
elseif x0>= 4
y= [ y, 2 ] ;
elseif x0>= 0
y= [ y, sqrt ( x0) ] ;
end
end
plot ( x, y)
axis ( [ 0 , 10 , 0 , 2.5 ] ) % 设置坐标轴
title ( '分段函数曲线' ) ; % 加图形标题
xlabel ( 'Variable X' ) ; % 加X轴说明
ylabel ( 'Variable Y' ) ; % 加Y轴说明
text ( 2 , 1.3 , 'y=x^{1/2}' ) ; % 在指定位置添加图形说明
text ( 4.5 , 1.9 , 'y=2' ) ;
text ( 7.3 , 1.5 , 'y=5-x/2' ) ;
text ( 8.5 , 0.9 , 'y=1' ) ;
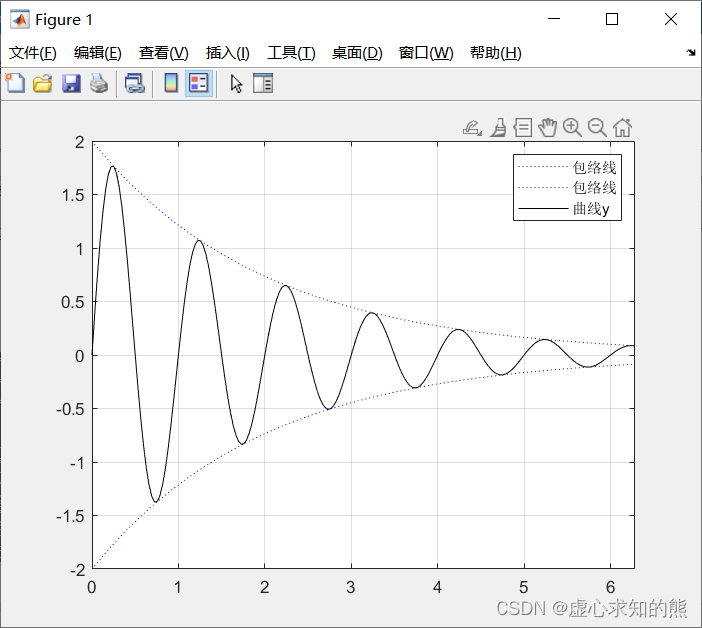
一般情况下,每执行一次绘图命令就刷新一次当前图形窗口,图形窗口原有图形将不复存在。 若希望在已存在的图形上再继续添加新的图形,可使用图形保持命令 hold。 hold on/off 命令控制是保持原有图形还是刷新原有图形,不带参数的 hold 命令在两种状态之间进行切换。例如,我们使用图形保持功能在同一坐标内绘制曲线
y
=
2
e
−
0.5
x
sin
(
2
π
x
)
y=2e^{-0.5x}\sin(2\pi x)
y = 2 e − 0.5 x sin ( 2 π x ) 程序如下: x= ( 0 : pi/ 100 : 2 * pi) ';
y1= 2 * exp ( - 0.5 * x) * [ 1 , - 1 ] ;
y2= 2 * exp ( - 0.5 * x) . * sin ( 2 * pi* x) ;
plot ( x, y1, 'b:' ) ; % 绘制两根包络线
axis ( [ 0 , 2 * pi, - 2 , 2 ] ) ; % 设置坐标
hold on; % 设置图形保持状态
plot ( x, y2, 'k' ) ; % 绘制曲线
legend ( '包络线' , '包络线' , '曲线y' ) ; % 加图例
hold off; % 关闭图形保持
grid % 网格线控制
在实际应用中,经常需要在一个图形窗口内绘制若干个独立的图形,这就需要对图形进行分割。分割后的图形窗口由若干个绘图区组成,每一个绘图区可以建立独立的坐标系制图形。同一图形窗口中的不同图形称为子图。 MATLAB 系统提供了 subplot 函数,用来将当前图形窗口分割成若干个绘图区。每个区域代表一个独立的子图,也是一个独立的坐标系,可以通过 subplot 函数激活某一区,该区为活动区,所发出的绘图命令都是作用于活动区域。 subplot 函数的调用格式如下:subplot ( m, n, p)
该函数将当前图形窗口分成
m
×
n
m×n
m × n
m
m
m
n
n
n
p
p
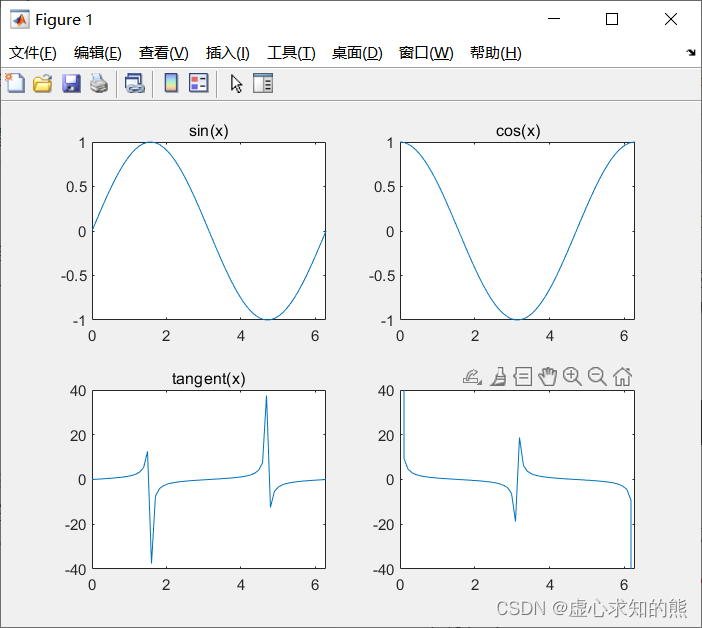
p 例如,我们在一个图形窗口中以子图形式同时绘制正弦、余弦、正切、余切曲线。 程序如下: x= linspace ( 0 , 2 * pi, 60 ) ;
y= sin ( x) ;
z= cos ( x) ;
t= sin ( x) . / ( cos ( x) + eps) ;
ct= cos ( x) . / ( sin ( x) + eps) ;
subplot ( 2 , 2 , 1 ) ; % 选择2 x2个区中的1 号区
plot ( x, y) ;
title ( 'sin(x)' ) ;
axis ( [ 0 , 2 * pi, - 1 , 1 ] ) ;
subplot ( 2 , 2 , 2 ) ; % 选择2 x2个区中的2 号区
plot ( x, z) ;
title ( 'cos(x)' ) ;
axis ( [ 0 , 2 * pi, - 1 , 1 ] ) ;
subplot ( 2 , 2 , 3 ) ; % 选择2 x2个区中的3 号区
plot ( x, t) ;
title ( 'tangent(x)' ) ;
axis ( [ 0 , 2 * pi, - 40 , 40 ] ) ;
subplot ( 2 , 2 , 4 ) ; % 选择2 x2个区中的4 号区
plot ( x, ct) ;
title ( 'cotangent(x)' ) ;
axis ( [ 0 , 2 * pi, - 40 , 40 ] ) ;
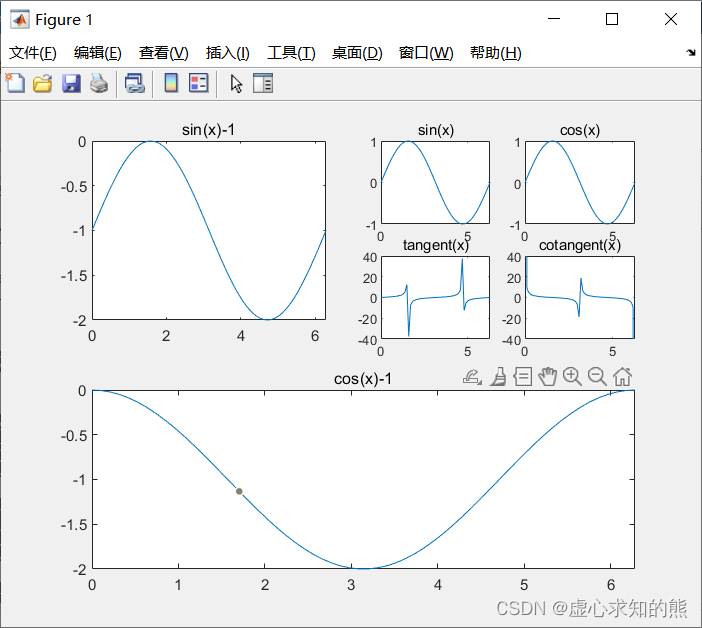
上例中将图形窗口分割成 2×2 个绘图区,编号从 1 到 4,各区分别绘制一幅图形,这是最规则的情况。但实际上,还可以进行更为灵活的分割,详见下面的程序(需要注意的是,图片的布局是以行为主,其次只需要数清每一个图的具体位置,大图小图不可以互相重叠)。 x= linspace ( 0 , 2 * pi, 60 ) ;
y= sin ( x) ;
z= cos ( x) ;
t= sin ( x) . / ( cos ( x) + eps) ;
ct= cos ( x) . / ( sin ( x) + eps) ;
subplot ( 2 , 2 , 1 ) ; % 选择2 x2个区中的1 号区
plot ( x, y- 1 ) ;
title ( 'sin(x)-1' ) ;
axis ( [ 0 , 2 * pi, - 2 , 0 ] ) ;
subplot ( 2 , 1 , 2 ) ; % 选择2 x2个区中的2 号区
plot ( x, z- 1 ) ;
title ( 'cos(x)-1' ) ;
axis ( [ 0 , 2 * pi, - 2 , 0 ] ) ;
subplot ( 4 , 4 , 3 ) ; % 选择4 x4个区中的3 号区
plot ( x, y) ;
title ( 'sin(x)' ) ;
axis ( [ 0 , 2 * pi, - 1 , 1 ] ) ;
subplot ( 4 , 4 , 4 ) ; % 选择4 x4个区中的4 号区
plot ( x, y) ;
title ( 'cos(x)' ) ;
axis ( [ 0 , 2 * pi, - 1 , 1 ] ) ;
subplot ( 4 , 4 , 7 ) ; % 选择4 x4个区中的7 号区
plot ( x, t) ;
title ( 'tangent(x)' ) ;
axis ( [ 0 , 2 * pi, - 40 , 40 ] ) ;
subplot ( 4 , 4 , 8 ) ; % 选择4 x4个区中的8 号区
plot ( x, ct) ;
title ( 'cotangent(x)' ) ;
axis ( [ 0 , 2 * pi, - 40 , 40 ] ) ;