快速傅里叶变换FFT在MATLAB中的实现
一、FFT的由来
首先,为什么要进行傅里叶变换?将时域的信号变换到频域的正弦信号,正弦比原信号更简单,且正弦函数很早就被充分地研究,处理正弦信号比处理原信号更简单。正弦信号的频率保持性:输入为正弦信号,输出仍是正弦信号,幅度和相位可能发生变化,但频率与原信号保持一致,只有正弦信号才拥有这样的性质。
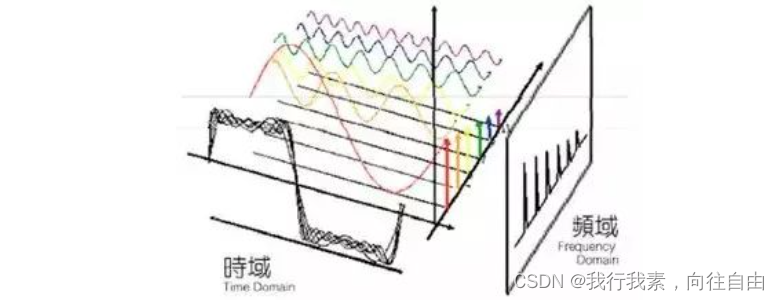
对于傅里叶变换的类型:非周期连续信号采用傅里叶变化;周期连续信号采用傅里叶级数;非周期连续离散信号采用离散时间傅里叶变换;周期离散信号采用离散傅里叶级数。
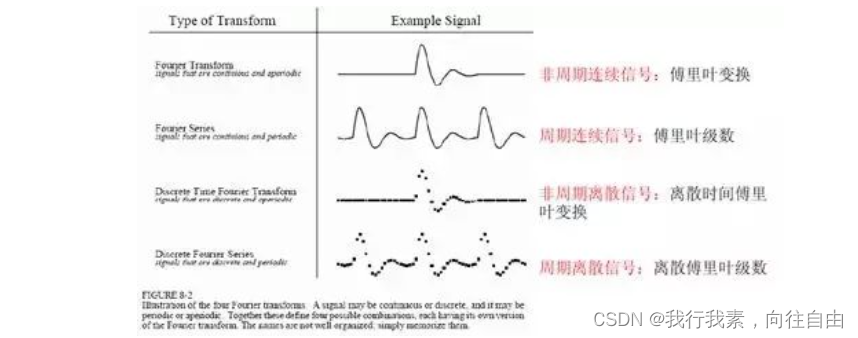
四种信号均为 (‐∞,+∞) 上的无穷信号,而计算机只能处理离散的、有限长度的信号。四种傅里叶变换总结如下表所示。
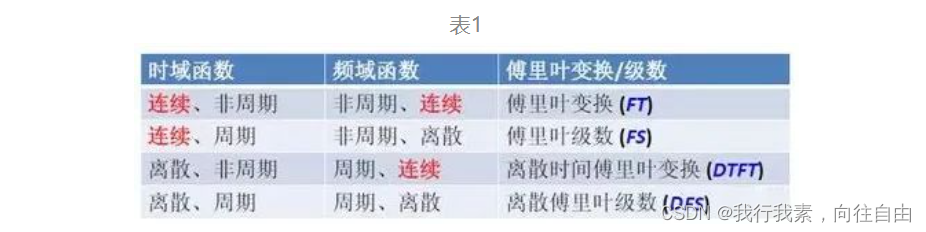
FT、FS、DTFT,至少都有一个域不是离散的,计算机无法处理;DFS满足时域和频率离散的要求,但其时域为无穷长的周期序列;通过对DFS的推导,得到适合计算机计算的离散傅里叶变换 (DFT)。
从离散傅里叶级数 (DFS) 到离散傅里叶变换 (DFT),周期序列虽为无穷长序列,但是只要知道一个周期的内容,便可知其全貌。因此,周期序列实际上只有N个样值有信息,通过推导可得到DFT、时域和频域 (DFT) 上的有限长序列,可以用来“代表”周期序列,DFT在时域和频域上均离散,且为有限长序列,可以用计算机进行处理。
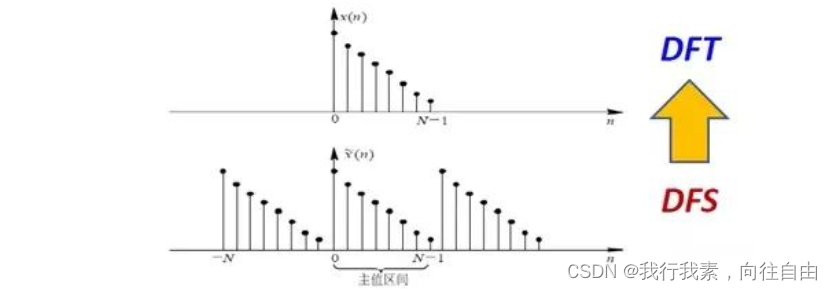
DFT虽好,但是其计算的次数太多,不利于大数据量的计算。FFT是DFT的快速算法可以节省大量的计算时间,其本质仍然是DFT。
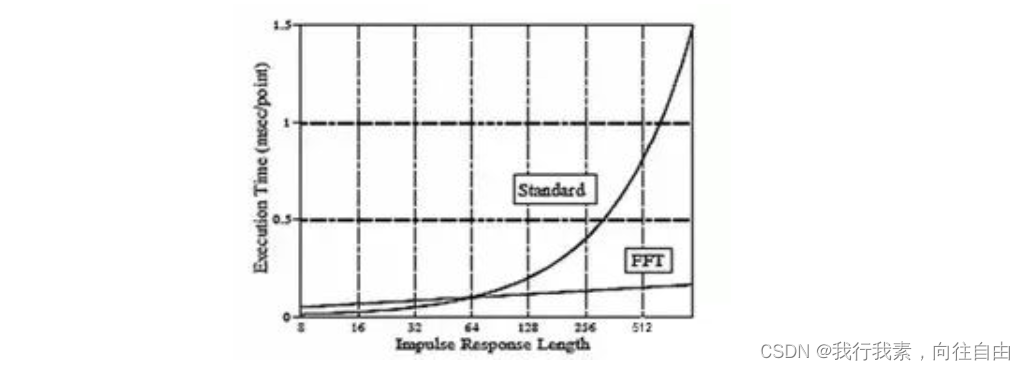
二、MATLAB中实现FFT 的计算
MATLAB傅里叶命令有两种:
-
Y= fft(x) ,其中,x 为一个序列(向量),存放采集信号的数据;
-
另外一种Y= fft(x,n),x 的定义同上,n 定义计算数据的个数,如果n 大于x 的长度,在x 的末尾添加0,使得x 的长度等于n。如果n小于x的长度,截取x 中的前n 个数来进行计算。Y 返回fft 的结果,为一个复数序列(向量),建议采用上一种格式的用法,并且保证 x 的个数为偶数。
FFT结果的数据长度:时域N 个点,频域为N/2+1个点;x 轴频率点的设置:采样频率为Fs 时,频谱图的最高频率为Fs/2(参照采样定理)。综合上述两点,x 轴的频率点为 (0:1:N/2)*Fs/N。


现对某一时域数据为例进行MATLAB傅里叶变换:
1. 绘制时域信号
lear;clc;closeall
a=textread('C:\Users\Administrator\Desktop\matlab\FFT\TIME_X.txt'); %读取时域数据
y=a(:,2); %读取时域数据
Fs=6400; %采集频率
T=1/Fs; %采集时间间隔
N=length(y); %采集信号的长度
t=(0:1:N-1)*T; %定义整个采集时间点
t=t'; %转置成列向量
figure
plot(t,y)
xlabel('时间')
ylabel('信号值')
title('时域信号')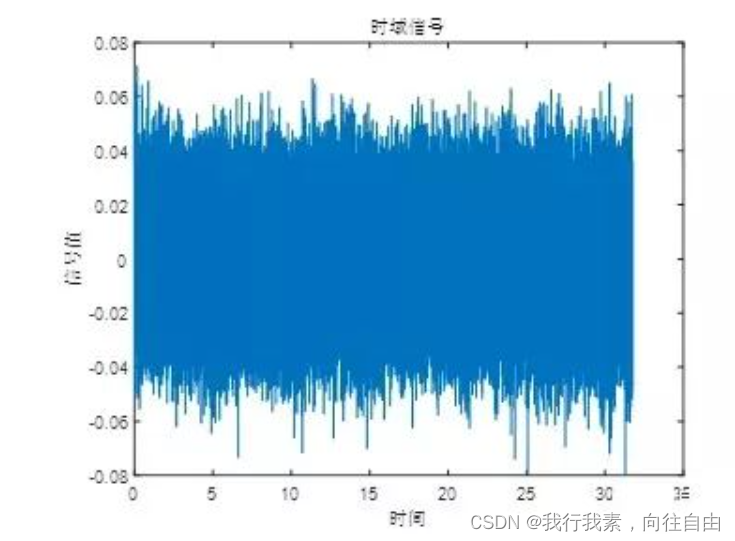
2. fft变换
Y=fft(y); %Y为fft变换结果,复数向量
Y=Y(1:N/2+1); %只看变换结果的一半即可
A=abs(Y); %复数的幅值(模)
f=(0:1:N/2)*Fs/N; %生成频率范围
f=f'; %转置成列向量3. 幅值修正
A_adj=zeros(N/2+1,1);
A_adj(1)=A(1)/N; %频率为0的位置
A_adj(end)=A(end)/N; %频率为Fs/2的位置
A_adj(2:end-1)=2*A(2:end-1)/N;4. 绘制频率幅值图和频谱相位图
figure
subplot(2,1,1)
plot(f,A_adj)
xlabel('频率(Hz)')
ylabel('幅值(修正后)')
title('FFT变换幅值图')
gridon
subplot(2,1,2)
phase_angle=angle(Y); %angle函数的返回结果为弧度
phase_angle=rad2deg(phase_angle);
plot(f,phase_angle)
xlabel('频率(Hz)')
ylabel('相位角(degree)')
title('FFT变换相位图')
grid on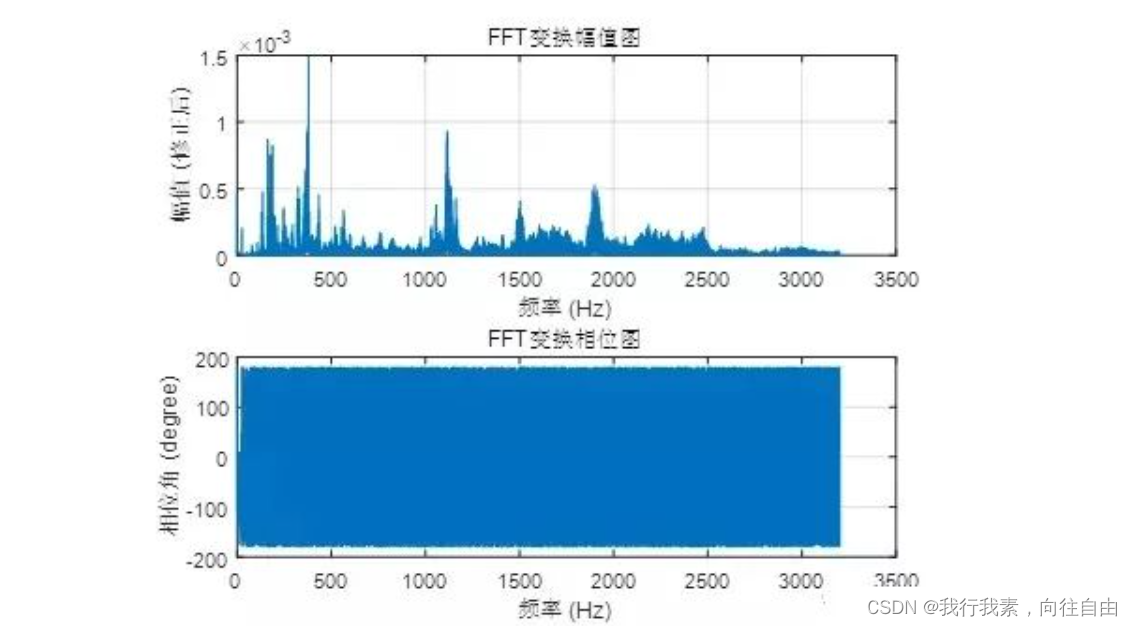
三、MATLAB中FFT计算和商业软件LMS Test.lab中FFT计算对比
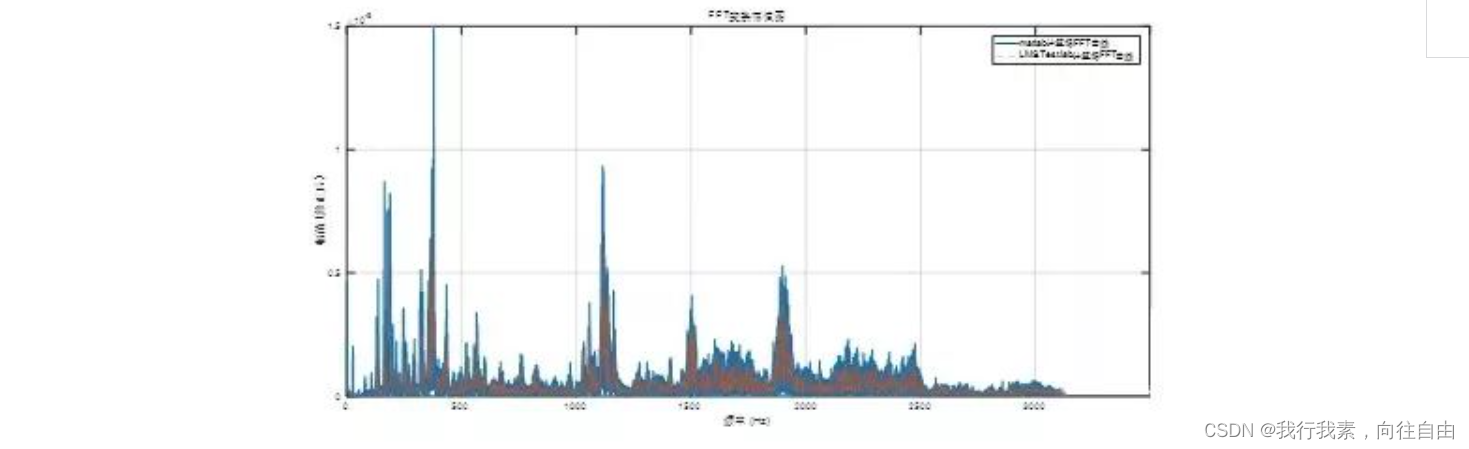
相同的时域数据,利用商业软件LMS Test.lab进行FFT计算,计算结果如下图所示。
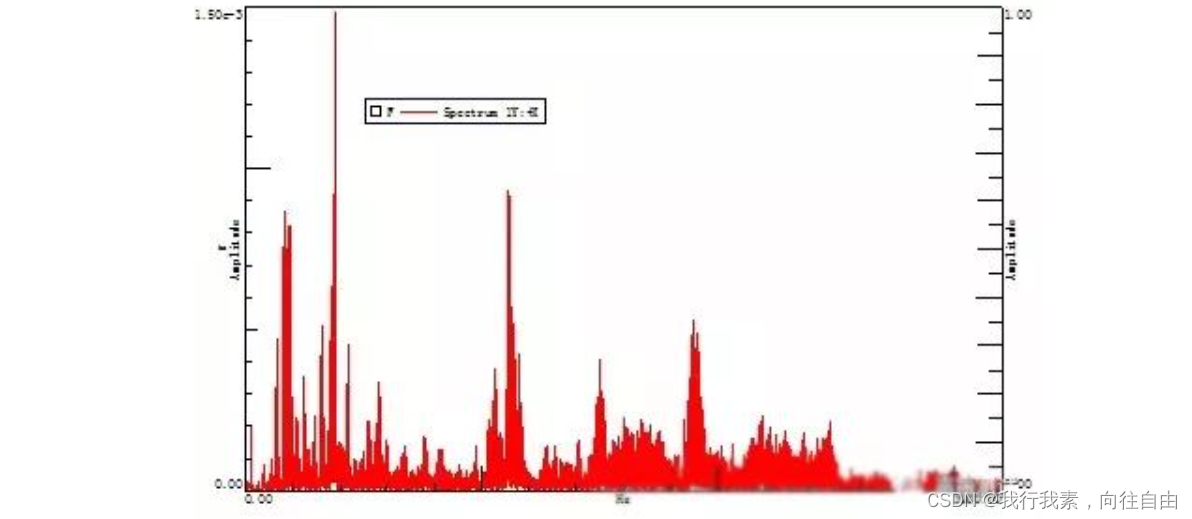
将matlab计算得频谱曲线和LMSTest.lab计算得频谱曲线放在同一图中对比,如下图所示。两种计算方式几乎完全重合,互相验证了计算方式的准确性。