弗洛伊德Floyd算法:代码详解及运行过程图解
#弗洛伊德算法:找到任意所有顶点到所有顶点的最短路径 #其实我觉得就是把迪杰斯特拉算法执行了n次,然后抽象出来,直接对图的邻接矩阵进行操作最终得到从所有结点到所有结点的最短路径
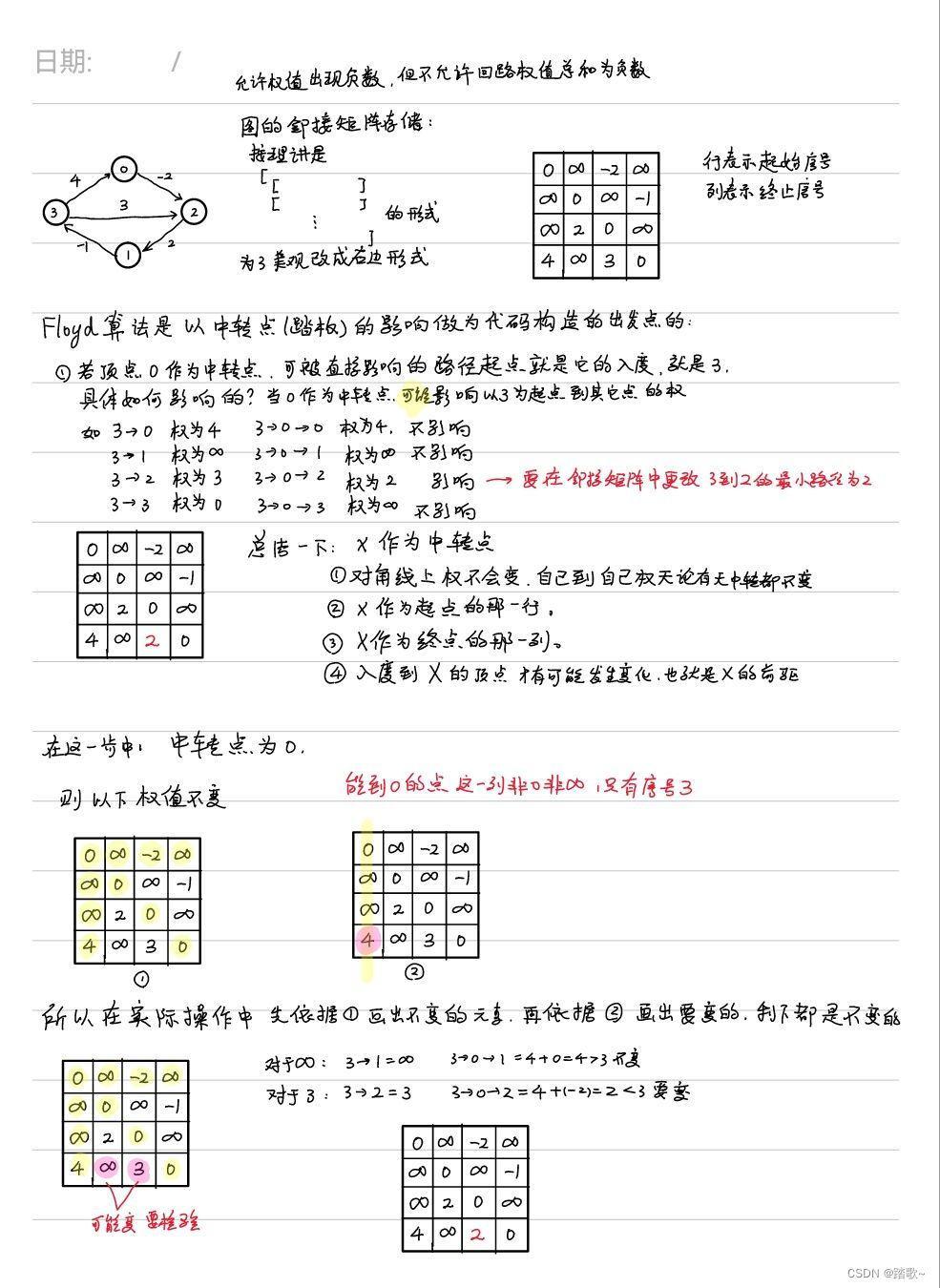
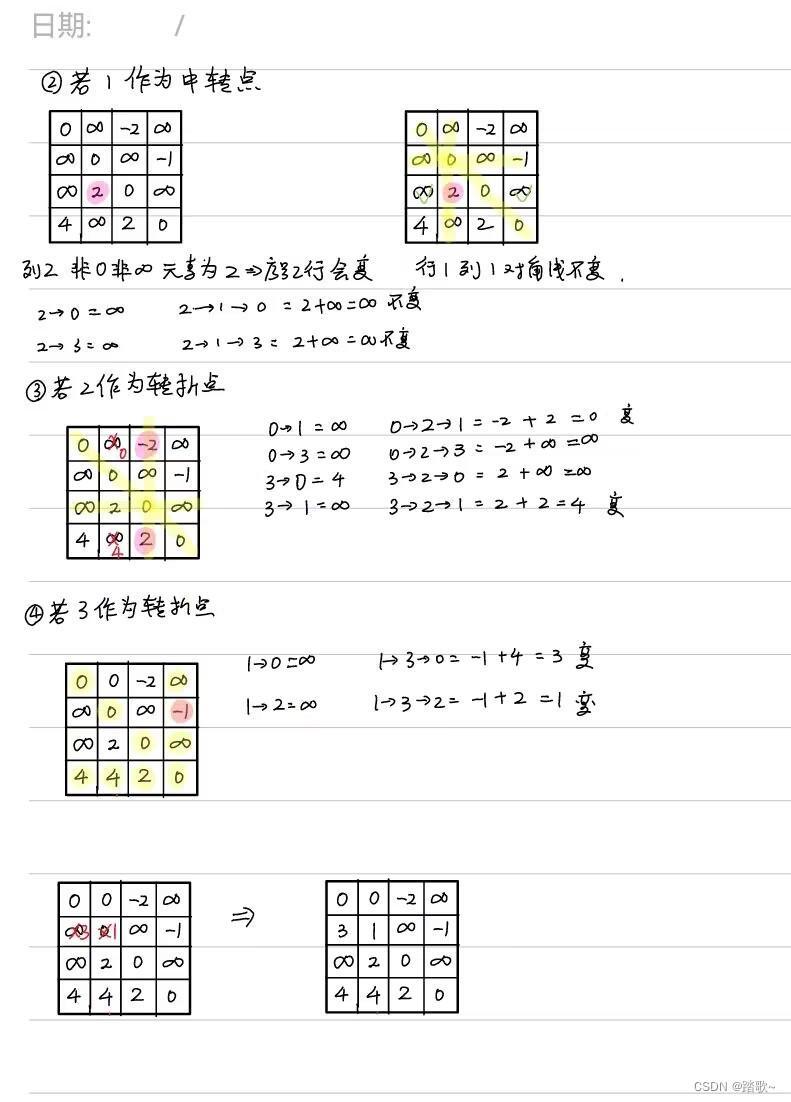
#弗洛伊德算法:找到任意所有顶点到所有顶点的最短路径
#其实我觉得就是把迪杰斯特拉算法执行了n次,然后抽象出来,直接对图的邻接矩阵进行操作最终得到从所有结点到所有结点的最短路径
def Floyd(g):
A=[[0]*MAXV for i in range(MAXV)]#用A存放之后的最短路径的邻接矩阵
path=[[0]*MAXV for i in range(MAXV)]
for i in range(g.n):
for j in range(g.n):
A[i][j]=g.edges[i][j]
if i !=j and g.edges[i][j]<INF:
path[i][j]=i#path仍然是到这个结点最短路径的前一个结点
else:
path[i][j]=-1
#k作为中转顶点去遍历每一个顶点,所以时间复杂度是n*n*n
for k in range(g.n):
for i in range(g.n):
for j in range(g.n):
if A[i][j]>A[i][k]+A[k][j]:#这一步得看图才能理解
A[i][j]=A[i][k]+A[k][j]
path[i][j]=path[k][j]
Dispath(A,path,g)
def Dispath(A,path,g):
for i in range(g.n):
for j in range(g.n):
if A[i][j]!=INF and i!=j:
print("顶点%d到%d的最短路径长度:%d \t路径:"%(i,j,A[i][j]),end='')
k=path[i][j]
apath=[j]
while k!=-1 and k!=i:
apath.append(k)
k=path[i][k]
apath.append(i)
apath.reverse()
print(apath)