minHash
寻找文本相似度Outline
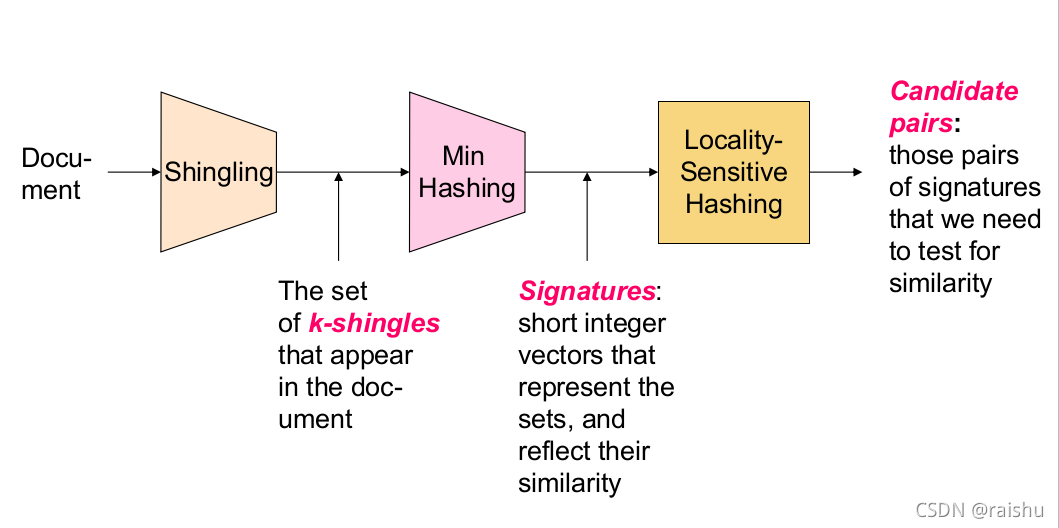
Shingling : 将文档转化成集合;
Minhashing : 将集合转化成较短签名,并保留集合间相似度;
Locality-sensitive hashing : 计算两两签名向量间的相似度。
Jaccard distance/similarity
Jaccard(A, B)= |A ∩ B| / |A ∪ B|
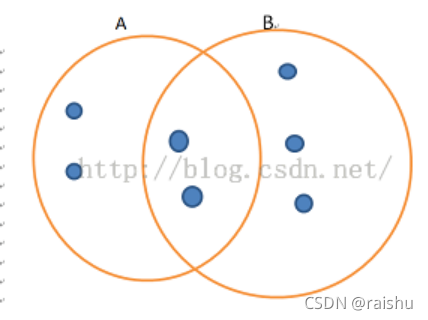
在上述例子中,sim(A,B)=2/7。
Shingling
A k-shingle (or k-gram) for a document is a sequence of k tokens that appears in the doc
(Tokens can be characters, words or something else, depending on the application)
直接举例子说明:
k=2,D1=abcab,那么2-shingles set:S(D1)={ab, bc, ca}
对于较长的shingle,可以将其hash.
For instance,to map 9-shingles to a bucket number of bucket in the range of 0-2^32-1
比如得到:h(D1)={1,5,7},
Next,两个文本的相似性可以用sim{set1,set2}表示
min-Hash
Shingles-Set的矩阵表示
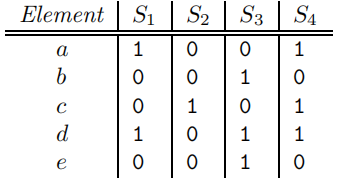
- Rows:一个元素在所有集合中的存在情况;
- Columns:集合;
- 当行e和列S为1时,表明元素e存在于集合S中;
- 两个集合的列相似度即Jaccard相似度就是两列的row为1的概率;
- 一般意义上,上述矩阵是稀疏的。所以存储这样的一个矩阵会浪费很多存储,因此我们需要将每列C哈希成较小的签名Sig{C},可以实现:
- Sig{C}足够小,可以把全部集合的签名放到内存;
- Sim(C1, C2)与Sim(Sig(C1), Sig(C2))近似。
minHash
minHash:将一个很大的集合进行哈希处理的过程其实是由很多小的哈希过程组成。而这些最小的哈希过程就被称为是最小哈希。最小哈希的具体内容就是把一个集合映射到一个编号上
比如对于集合U={a,b,c,d,e}, S1={a,d}, S2={c}, S3={b,d,e}, S4={a,c,d},我们用一个矩阵形式来表示的话就是:

那么,对他进行一次最小哈希就是在经过随机的行排列之后,对于每个集合,从上到下取第一个数值为1的那一行的行号。
比如对上面的矩阵进行随机行排列后变成:
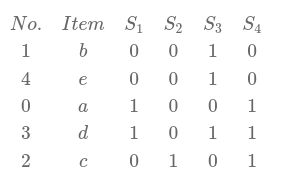
那么每个集合的minhash结果就应该是h(S1)=0, h(S2)=2, h(S3)=1,h(S4)=0。
这就是minhash的基本方法。
minHash signatures
在最小哈希的基础上,最小哈希签名也就很简单了。在最小哈希中,需要对每行进行随机行排列,如果是真随机排列的话显然计算消耗会特别大。因此实际上我们采用了一个替代方法,就是再用一个哈希函数,将行号进行哈希变换。比如当n=5时,对0,1,2,3,4这5个数,可以用h(x) = 3x+1的方法进行映射,得到1,4,2,0,3。当然,随便找的h(x)=ax+b这种哈希函数显然可能会冲突,不过只要n和a互素,那么生成的一定是一个排列,这一点用同余类的知识很好证明。
不过显然,一次最小哈希的结果不能全面的表现出集合的特征。因此最小哈希签名采用了k个不同的哈希函数h1,h2,h3…hk; 对于集合S,分别调用这些函数作为最小哈希的排列函数,构建出集合S的最小哈希签名[h1(S),h2(S),h2(S)…,hk(S)]
显然,这个签名所占的空间要远远小于用朴素的方法保存集合所需的空间。
保留相似度的Hash
但是,我们为什么可以这样做?为什么MinHash保留了相似性呢?因为两列的最小hash值就是这两列的Jaccard相似度的一个估计,换句话说,两列最小hash值同等的概率与其相似度相等,即P(h(Si)=h(Sj)) = sim(Si,Sj),证明如下:
对于任意i, j两列,他们可能:
都是1——有A行
既有1,又有0——有B行
对于i, j的Jaccard similarity:
sim = A/B
那么对于MinHash来说, 随机排列后:
从上往下数同时为1的行比一个为1一个为0的行先出现的概率就是A/B
所以,算出了MinHash,并得到signature,原先的相似性也保留在了signature当中
为什么我们需要MinHashing Signature呢?因为中心极限定理。一次hash只是偶然,多次hash才能接近概率。这也是为什么我们用了h1,h2,h3三个hash函数。在实际应用中,会使用更多的hash函数
可以发现,原先一个可能非常大的文章,被我们摘要成了一个签名矩阵,同时不同文章之间的相似性却保留下来了。
Locality Sensitive Hashing(LSH)
通过上面的方法处理过后,一篇文档可以用一个很小的签名矩阵来表示,节省下很多内存空间;但是,还有一个问题没有解决,那就是如果有很多篇文档,那么如果要找出相似度很高的文档,其中一种办法就是先计算出所有文档的签名矩阵,然后依次两两比较签名矩阵的两两;这样做的缺点是当文档数量很多时,要比较的次数会非常大。那么我们可不可以只比较那些相似度可能会很高的文档,而直接忽略过那些相似度很低的文档。接下来我们就讨论这个问题的解决方法。
首先,我们可以通过上面的方法得到一个签名矩阵,然后把这个矩阵划分成b个行条(band),每个行条由r行组成。对于每个行条,存在一个哈希函数能够将行条中的每r个整数组成的列向量(行条中的每一列)映射到某个桶中。可以对所有行条使用相同的哈希函数,但是对于每个行条我们都使用一个独立的桶数组,因此即便是不同行条中的相同列向量,也不会被哈希到同一个桶中。这样,只要两个集合在某个行条中有落在相同桶的两列,这两个集合就被认为可能相似度比较高,作为后续计算的候选对;
下面直接看一个例子:
例如,现在有一个12行签名矩阵,把这个矩阵分为4个行条,每个行条有3行;为了方便,这里只写出行条1的内容。
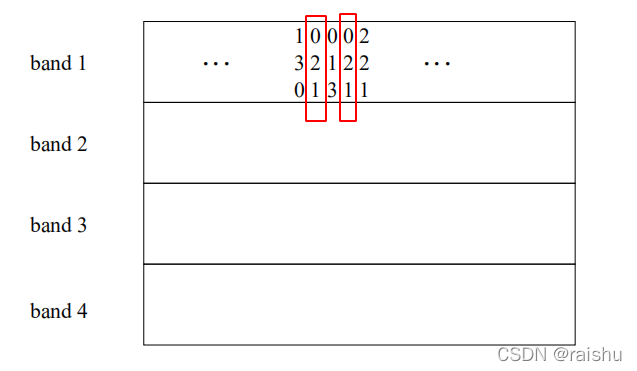
可以看出,band 1中第2列和第4列的内容都为[0,2,1],所以这两列会落在band 1下的相同桶中,因此不过在剩下的3个行条中这两列是否有落在相同桶中,这两个集合都会成为候选对。在band 1中不相等的两列还有另外的3次机会成为候选对,因为他们只需在剩下的3个band中有一次相等即可。
经过上面的处理后,我们就找出了相似度可能会很高的一些候选对,接下来我们只需对这些候选队进行比较就可以了,而直接忽略那些不是候选对的集合