leetcode练习笔记2022年9月

C语言常用函数库：

快速排序

<stdlib>: qsort

补充使用简介：
https://blog.csdn.net/ZDDWLIG/article/details/120209948

具体如下

• 普通数组
• 二维数组
• 二维指针数组

#include <stdio.h>
#include <stdlib.h>


int cmp1(const void*a, const void*b)
{
	return (*((int*)a) - *((int*)b));
}

int cmp2(const void*a, const void*b)
{
	int *ax = (int*)a;
	int *bx = (int*)b;
	if(ax[0] != bx[0]) {
		return (ax[0] - bx[0]);
	}
	return (ax[1] - bx[1]);
}

int cmp3(const void*a, const void*b)
{
	int *ax = *(int**)a;
	int *bx = *(int**)b;
	if(ax[0] != bx[0]) {
		return (ax[0] - bx[0]);
	}
	return (ax[1] - bx[1]);
}

int main()
{
	printf("一维数组\n");

	int a[3] = { 3, 1 , 2};
    qsort(a, sizeof(a)/sizeof(int), sizeof(int), cmp1);
	for(int i = 0; i < 3; i++) {
        printf("%d\n", a[i]);
	}

    printf("二维数组\n");
	int b[3][2] = { {3, 1} , {2, 2}, {2, 1}};
    qsort(b, sizeof(b)/sizeof(b[0]), sizeof(b[0]), cmp2);
	for(int i = 0; i < 3; i++) {
        printf("%d %d\n", b[i][0], b[i][1]);
	}

	printf("二维数组指针\n");
	int c[3][2] = { {3, 1} , {2, 2}, {2, 1}};
	int *d[3] = { c[0], c[1], c[2]};

    qsort(d, sizeof(d)/sizeof(d[0]), sizeof(d[0]), cmp3);
	for(int i = 0; i < 3; i++) {
        printf("%d %d\n", d[i][0], d[i][1]);
	}

	return (0);
}

---

求最大最小值

<math.h>: fmax/fmin

---

需要重点学习的算法

周赛题目练习中遇到的经典算法记录：

参考：https://leetcode.cn/problems/divide-intervals-into-minimum-number-of-groups/solution/by-lfool-iri7/

「贪心 + 堆」「线段树」「差分数组」

差分数组：

参考博客《基础算法：差分讲解》

1.差分的基本概念：

如果有一数列 a[1],a[2],.…a[n]且令 b[i]=a[i]-a[i-1],b[1]=a[1]

那么就有

• a[i]=b[1]+b[2]+.…+b[i] = a[1]+a[2]-a[1]+a[3]-a[2]+.…+a[i]-a[i-1]
  此时b数组称作a数组的差分数组

• 换句话来说a数组就是b数组的前缀和数组 例：
  原始数组a：9 3 6 2 6 8
  差分数组b：9 -6 3 -4 4 2
  可以看到a数组是b的前缀和

• 现在需求：将[l,r]区间中的数组元素a[i]均加上常数C，如果使用原始算法，则要扫描一下数组a，时间复杂度为O(n)；如果使用差分算法则时间复杂度仅为O(1)。具体步骤如下：
  a.b[l] + C：当b[l] + C时，a[l]、a[l+1]、…、a[n]均会加C，原因是a[i] = b[1] + b[2] + … + b[i]
  b.b[r + 1] - C：由于需求是将数组a中[l,r]区间中的元素均加C，因此需要将b数组中a[r+1, n]区间中的元素都减去C。这样做才能够抵消b[l] + C步骤中将数组a中[r + 1, n]区间中的元素多加的C给抵消掉，实现真正将[l,r]区间中的数组元素a[i]均加上常数C. 引用

2. 差分数组应用练习题

例题1：有n个数，m个操作,每一次操作，将x~y区间的所有数增加z；
最后有q个询问，每一次询问求出x~y的区间和。

分析：首先我们得到一个原数组a，然后
设d[i]=a[i]-a[i-1] (1<i≤n,d[1]=a[1])；//差分数组
设f[i]=f[i-1]+d[i] (1<i≤n,f[1]=d[1]=a[1])；
设sum[i]=sum[i-1]+f[i] (1<i≤n,sum[1]=f[1]=d[1]=a[1])。//区间求和

例题2： 同样利用差分数组对某一区间的值进行修改，sum数组保存的就是前n项的和
只对区间两端的值进行修改，是因为每次的 f[i] 数组都包含着 f[i-1]+d[i],即如果在修改区间[left,right]内的话，从区间left开始以后的每一项都加上了修改值z，然后到最后一项right+1时就把z减掉

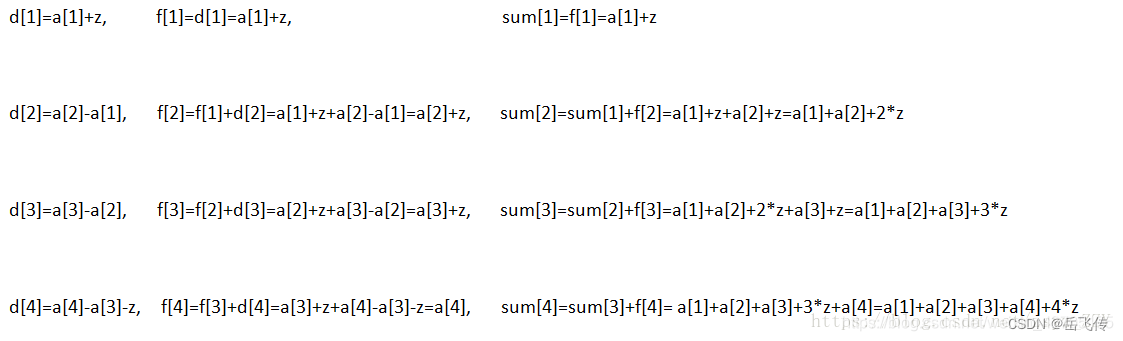
具体代码如下：

#include <stdio.h>
#include <stdlib.h>

#define N 10


int main()
{
	int a[N] = {1,2,3,4,5,6,7,8,9,0};
	int b[N] = {0};
	int f[N] = {0};
	int sum[N] = {0};
	int m = 3;
	int q = 2;
	b[0] = a[0];

    for (size_t i = 1; i < N; i++) {
		b[i] = a[i] - a[i-1];//差分数组
	}
	for(int i = 0, x, y, k; i < m; i++) {
        scanf("%d %d %d", &x, &y, &k);//区间x~y m个操作加k
		b[x] += k;
		b[y+1] -= k;
	}
    for (size_t i = 1; i < N; i++) {
		f[i] = f[i-1] + b[i]; //相当于原始数组a
		sum[i] = sum[i-1] + f[i];//求a[i]的前缀和
	}

	for (int i = 0, x, y; i < q; i++) {
		scanf("%d %d", &x, &y);
		printf("询问：%d ~ %d 之间的和是 %d", x, y, sum[y] - sum[x-1]);
	}
	
	return (0);
}

---