初步了解TensorFlow如何实现正则化

为了避免过拟合问题，一个非常常用的方法是正则化（regularization），正则化的思想就是在损失函数中加入刻画模型复杂程度的指标。

假设用于刻画模型在训练数据上表现的损失函数为J(θ)，那么在优化时不是直接优化J(θ)，而是优化J(θ) + λR(w)，其中R(w)刻画的是模型的复杂程度，而λ表示模型复杂损失在总损失中的比例，需要注意的是，这里的θ表示的是一个神经网络中所有的参数，它包括边上的权重w和偏置项b，但一般来说模型复杂度只由权重w决定。

常用的刻画模型复杂度的函数R(w)有两种，一种是L1正则化，计算公式是：

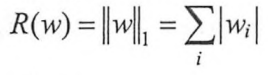
另一种是L2正则化，计算公式是：

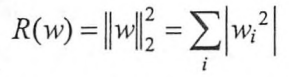
TensorFlow可以优化任意形式的损失函数，所以TensorFlow自然也可以优化带正则化的损失函数。

L1正则化和L2正则化，在TensorFlow中分别以不同的函数实现它们，以下列代码为示例：

#含有L1正则化的损失函数：
loss = tf.reduce_mean(tf.square(y_ - y)) + tf.contrib.layers.l1_regularizer(λ)(w)

#含有L2正则化的损失函数：
loss = tf.reduce_mean(tf.square(y_ - y)) + tf.contrib.layers.l2_regularizer(λ)(w)

1. loss为定义的损失函数，它由两个部分组成，第一个部分是均方误差损失函数，它刻画了模型在训练数据上的表现，第二个部分就是正则化，它防止模型过度模拟训练数据中的随机噪音；

2. λ表示了正则化项的权重，w为需要计算正则化损失的参数。

TensorFlow提供了tf.contrib.layers.l1_regularizer函数和tf.contrib.layers.l2_regularizer函数用来计算L1正则化和L2正则化，通过以下代码给出使用两个函数的样例：

import tensorflow as tf

weights = tf.constant([[1.0, -2.0], [-3.0, 4.0]])

with tf.Session() as sess:
    #计算结果为5.0
    print(sess.run(tf.contrib.layers.l1_regularizer(0.5)(weights)))
    #计算结果为15 * 1/2 = 7.5，L2正则化乘以1/2可以方便求导
    print(sess.run(tf.contrib.layers.l2_regularizer(0.5)(weights)))

在简单的神经网络中，这样的方式就可以很好地计算带正则化的损失函数了，但当神经网络的参数增多之后，这样的方式首先可能导致损失函数loss的定义很长，可读性差且容易出错，更主要的是，当网络结构复杂之后定义网络结构的部分和计算损失函数的部分可能不在同一个函数中，这样通过变量这种方式计算损失函数就不方便了。

为了解决这个问题，可以使用TensorFlow中提供的集合（collection）来维护需要计算的正则化损失，以下列代码为示例给出通过集合计算一个5层神经网络带L2正则化的损失函数的计算方法：

import tensorflow as tf

#获取一层神经网络边上的权重，并将这个权重的L2正则化损失加入名称为losses的集合中
def get_weight(shape, r):
    #生成一个变量
    var = tf.Variable(tf.random_normal(shape, stddev=1, seed=1), dtype=tf.float32)
    '''add_to_collection函数将这个新生成变量的L2正则化损失项加入集合
    这个函数的第一个参数losses是集合的名字，第二个参数是要加入这个集合的内容'''
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(r)(var))
    return var

x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

#定义了每一层网络中节点的个数
layer_dimension = [2, 10, 10, 10, 1]
#神经网络的层数
n_layers = len(layer_dimension)

#这个变量维护前向传播时最深层的节点，开始的时候就是输入层
cur_layer = x
#in_dimension为当前层的节点个数
in_dimension = layer_dimension[0]

#通过一个循环来生成5层全连接的神经网络结构
for i in range(1, n_layers):
    #out_dimension为下一层的节点个数
    out_dimension = layer_dimension[i]
    #生成当前层中权重的变量，并将这个变量的L2正则化损失加入losses集合
    weight = get_weight([in_dimension, out_dimension], 0.001)
    bias = tf.Variable(tf.fill([1, out_dimension], 0.1))
    #使用ReLU激活函数
    cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias)
    #进入下一层之前将下一层的节点个数更新为当前层节点个数
    in_dimension = out_dimension

'''在定义神经网络前向传播的同时已经将所有的L2正则化损失加入了losses集合
这里只需要计算刻画模型在训练数据上表现的损矣函数。'''
mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))

#将均方误差损失函数加入损失集合
tf.add_to_collection('losses', mse_loss)

'''get_collection返回一个列表，这个列表包含所有这个集合中的元素
在这个样例中这些元素就是损失函数的不同部分，将它们加起来就可以得到最终的损失函数。'''
loss = tf.add_n(tf.get_collection('losses'))