随机梯度下降算法学习笔记

梯度下降的常用领域：

 

线性回归：

 

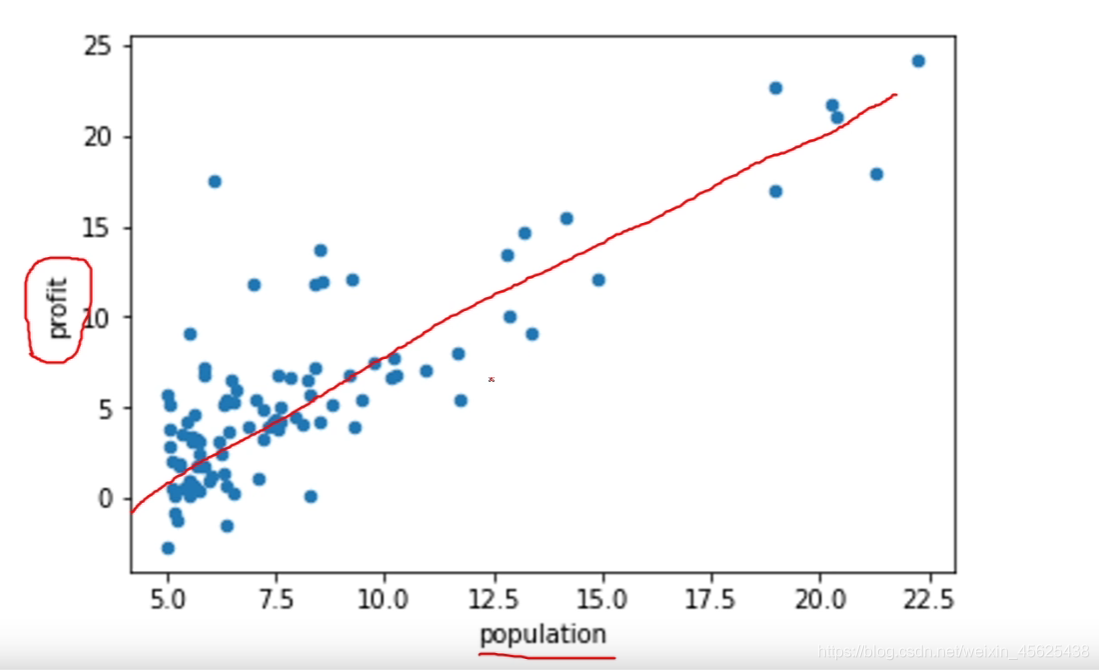
例如：利用线性回归预测不同人口数量的城市下开饭馆的利润趋势。

损失函数

 

梯度

 

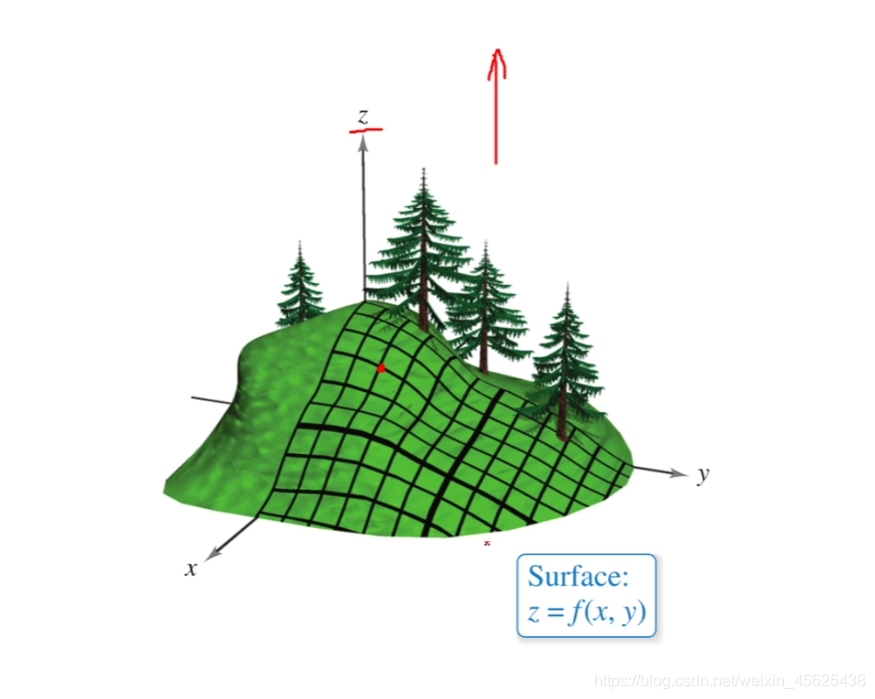
Z轴越大，损失越大，也就是我们要从山顶下到山脚。

可以将梯度理解为下山的方向（损失函数的偏导），当红点到山脚时，得到算法的最优结果。

 

梯度下降算法思路：

while 循环：

梯度=gradient（θ0，θ1）

（θ0，θ1）=（θ0，θ1）- 梯度*学习率    //  用减法表示下坡。

学习率可以理解为下山时步伐的大小，在编程时需要不断调试学习率的大小，太大或者太小都不好。

太大容易反复横跳；太小步伐太小，计算次数太多。

 

最后附上代码：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

path = 'C:\\Users\\Administrator\\Desktop\\data.txt'
data = pd.read_csv(path, header=None)
plt.scatter(data[:][0], data[:][1], marker='+')
data = np.array(data)
m = data.shape[0]
theta = np.array([0, 0])
data = np.hstack([np.ones([m, 1]), data])
y = data[:, 2]
data = data[:, :2]


def cost_function(data, theta, y):
    cost = np.sum((data.dot(theta) - y) ** 2)
    return cost / (2 * m)


def gradient(data, theta, y):
    grad = np.empty(len(theta))
    grad[0] = np.sum(data.dot(theta) - y)
    for i in range(1, len(theta)):
        grad[i] = (data.dot(theta) - y).dot(data[:, i])
    return grad


def gradient_descent(data, theta, y, eta):
    while True:
        last_theta = theta
        grad = gradient(data, theta, y)
        theta = theta - eta * grad
        print(theta)
        if abs(cost_function(data, last_theta, y) - cost_function(data, theta, y)) < 1e-15:
            break
    return theta


res = gradient_descent(data, theta, y, 0.0001)
X = np.arange(3, 25)
Y = res[0] + res[1] * X
plt.plot(X, Y, color='r')
plt.show()

该代码需要导入原始数据，最终会得到如上图所示的线性回归图