【L2】深蓝学院-高飞老师 移动机器人规划笔记 基于搜索的路径规划

相关概念

配置（Configuration）

对机器人上面所有的点的位置的描述

自由度（degree of freedom，DOF）

用最少的坐标的数量去表示机器人存在的配置

配置空间（Configuration Space）

有n个维度的空间中，包含了所有的机器人可能存在的位姿。

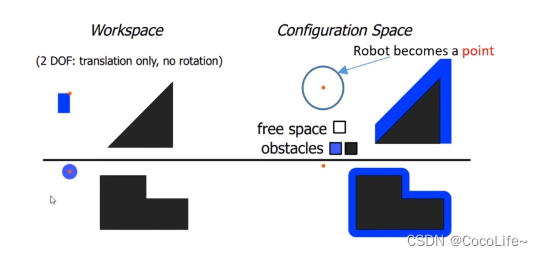
在配置空间中做规划

在配置空间中做规划要比在朴素的空间中做优化要容易，因此需要将障碍物转换到配置空间中，成为c-obstacles，简单来讲，一般都是把有形状的机器人转换为点，然后把障碍物去做对应尺寸的膨胀，问题就变成了点的规划，就不用考虑机器人的尺寸了。

图搜索的概念

图的概念与图神经网络里面的图是一样的，之前搞过就没有记~

图的构成方式

如果是基于搜索的方法，本身的每一个格子都和其他相邻格子有物理概念上的连接，因此本身就是一种图。基于采样的方法，其中就没有这样物理概念上的连接，往往需要人为的利用采样生成的节点构图。

图搜索

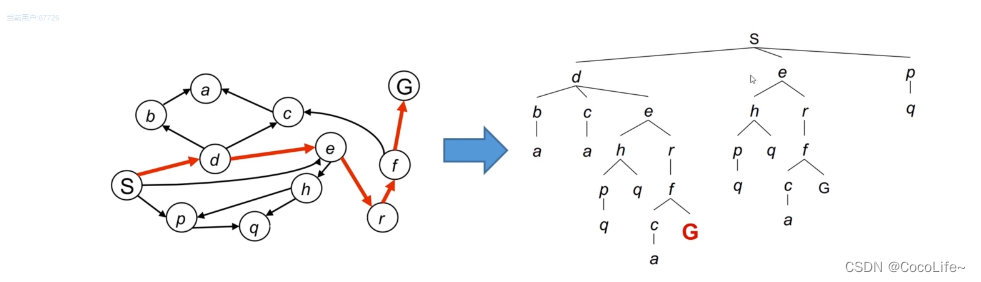
图搜索总是从一个起始状态开始，会产生一个搜索树，如下图所示。回推整个搜索的过程也就得到了一个所谓的路径，当然在机器人规划时，完整的搜索是很费力的，那如何尽可能快地完成最优搜索也就是后续需要研究的重点。

图搜索方法的整体框架

总是维护一个容器：这个容器装载了将来有可能或打算访问的所有节点。值得注意的是，该容器一开始是空的，第一个放入的就是设定的起始节点。随后进入循环：

1. 进入循环：在容器里，根据实现给定的指标或目的，弹出一个节点（访问一个节点）；
2. 扩展：发现其所有存在的邻居节点；
3. 把扩展的新的节点放入容器中，直到完成目标或其他指标后终止循环。

那么这其中涉及到一些其他问题，比如：

• 什么时候循环停止呢？
  一个比较直观的答案是当容器中没有节点时就停止。
• 那如果存在整个图是一个循环的结构的呢？
  这时为了避免图搜索陷入死循环，往往还会维护另外一个新的容器（close list 闭集），这个容器装载着被访问过的节点，保证不会被再次访问。
• 按照什么规则去访问节点去尽可能快地到达目标节点呢？
  这个就涉及到后续介绍的算法啦！

图遍历的方法（Graph traversal）

这里是后面算法的基础~包含最经典的广度优先搜索算法和深度优先搜索算法。如下图：

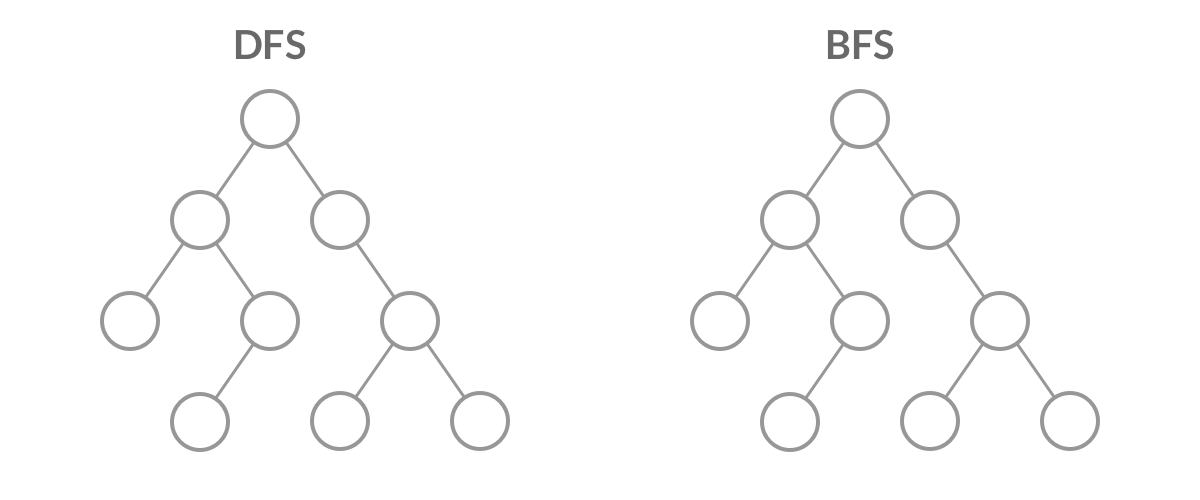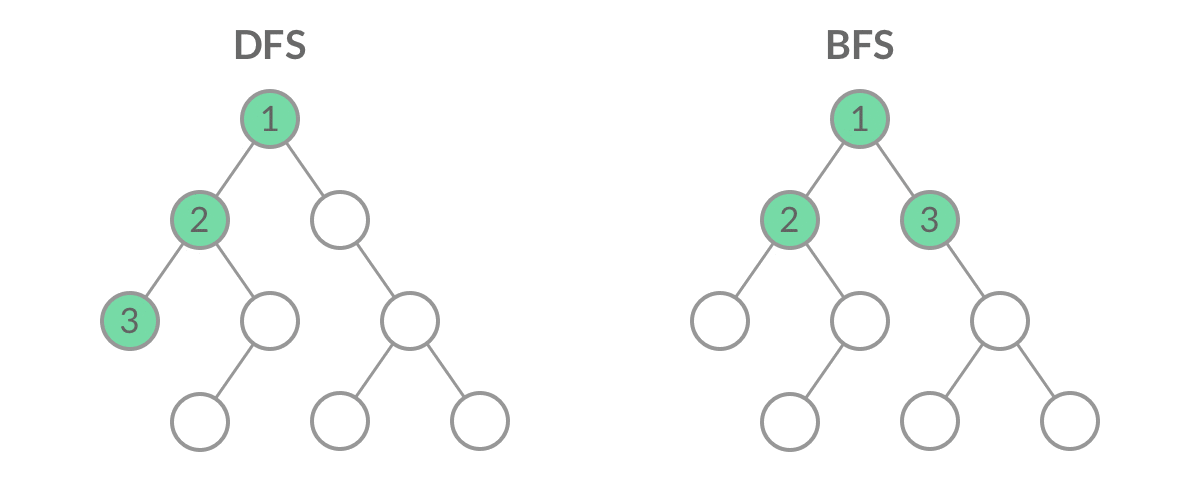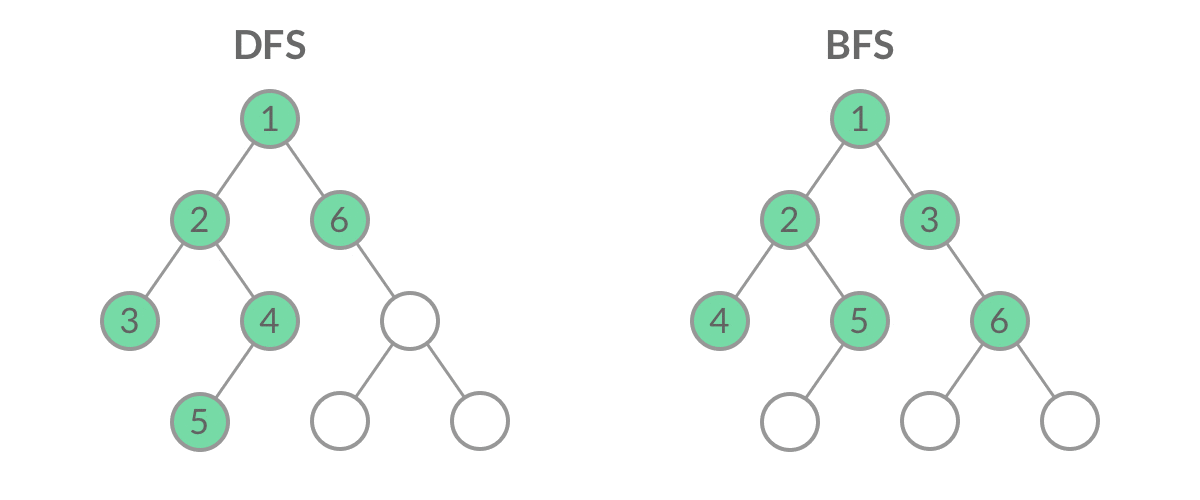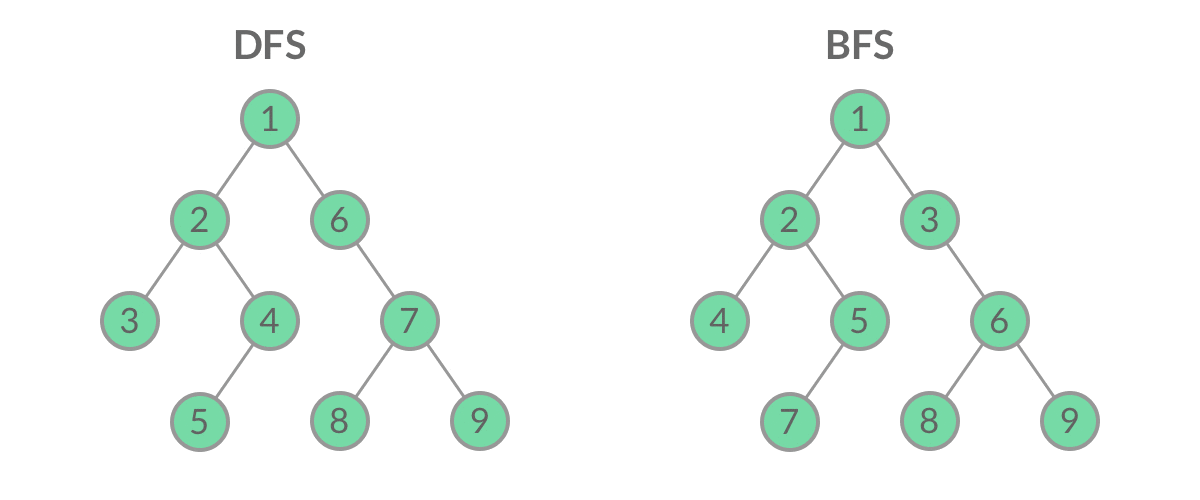
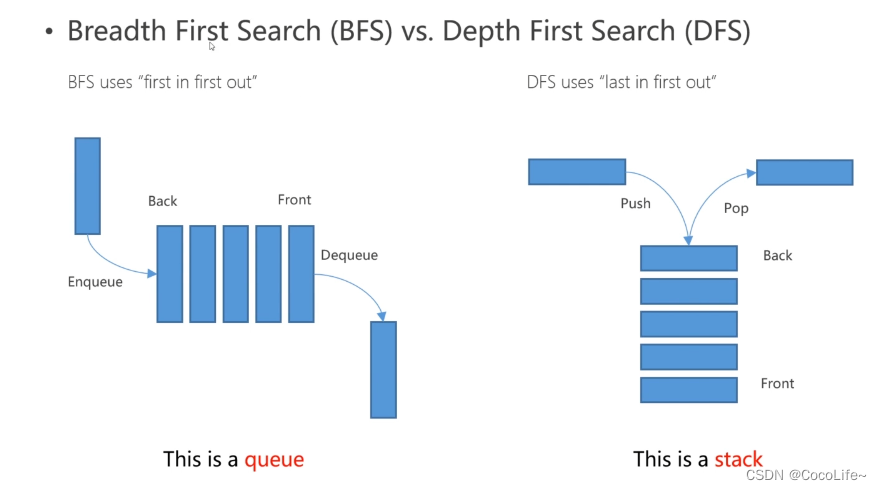
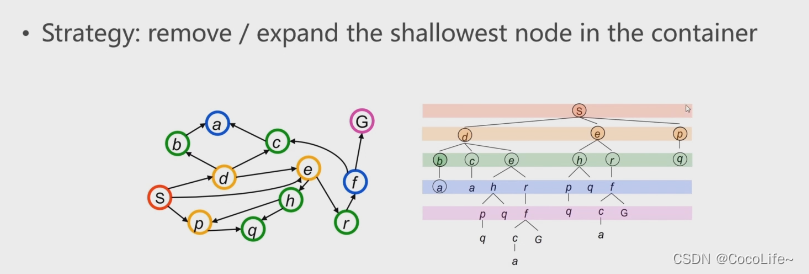
• 广度优先搜索（Breadth First Search，BFS）：遵从先进先出原则，是一个队列（容器）。从下图可以理解到，容器优先遍历完最浅的一层的节点后才回去访问更深层的节点。
  
  

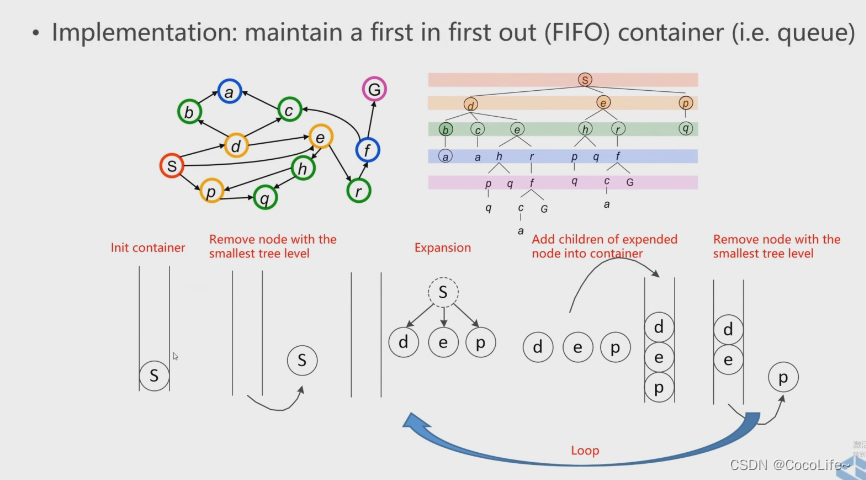
• 深度优先搜索（Depth First Search，DFS）：遵从后进先出原则，是一个堆栈（容器）。从下图可以理解到，容器先弹出已有节点中最深层级的节点，也就是优先把一条路径走到底。
  
  

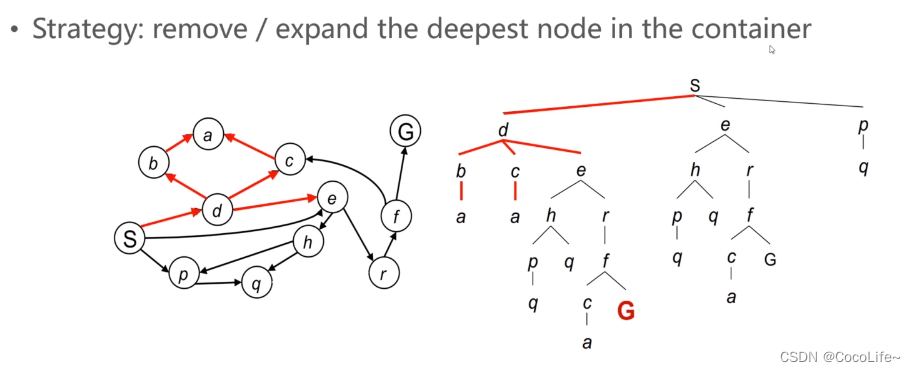
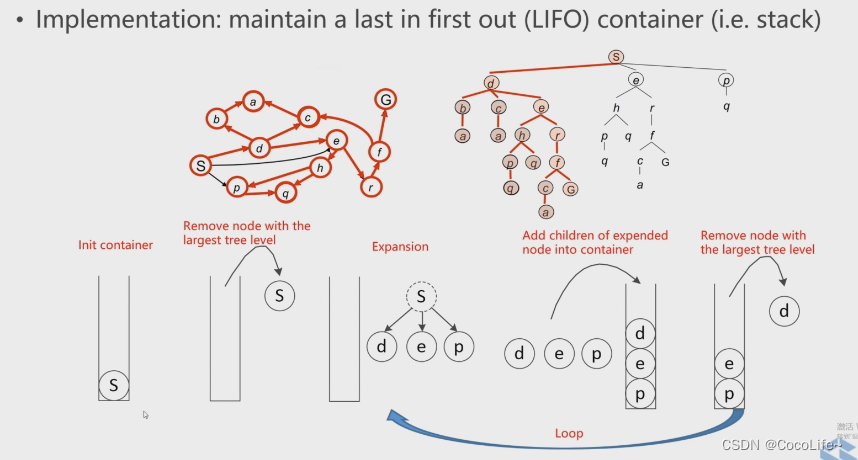
上述两种方法对比来看，对于选择最优化路径这个任务而言，目前可以更多关注广度优先搜索算法，原因可以从下图看出，BFS虽然搜索的可能会比较慢，但是搜索到目标终点后回溯一定是可以得到较好的路径的，但是DFS是一条路走到黑的搜索方式，得到的路径结果就不一定符合我们的预期了。

启发式的搜索算法（heuristic search）

这里主要介绍了贪心算法。区别于BFS的先进先出和DFS的后进先出，贪心算法的弹出策略是人为去规定的，heuristic是一个对于目前与终点之间距离的猜测（忽视障碍物的欧氏距离或x、y轴分别距离和的曼哈顿距离等），因此可以启发路径搜索通往较优的方向。
然而，贪心算法并不一定会比BFS搜索方法要好，看起来在无障碍地情况下，贪心算法搜索确实有着明显的优势，即更快的找到与BFS搜索得到的同样最优的路径，但是在有障碍物的情况下，heuristic的指引也有可能使算法陷入路径上的局部最优解。

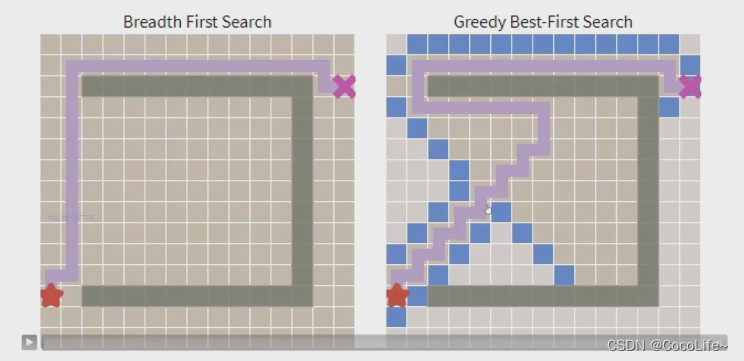
上述搜索方法的缺陷

上述的DFS，BFS，贪心算法能够正确搜索到路径的前提是没有考虑建成的图之中各个边所代表的不同权重，也就是所谓的路径的cost，但是在实际的工程情况中，不同的边的飞行代价是不一样的，可能涉及到长度、飞行时长、能量消耗等考虑因素，因此需要设计更普适的找到最小代价路线的搜索算法。

Dijkstra 算法

• 弹出原则是：每次弹出的节点具备最小的cost g（n），g（n）表示的是，从起点出发到当前节点积累的cost。
• 会更新n节点的所有未被扩展的邻居节点m，如果从n到m这个走向的g（m）比原来的cost小的话，就会做一个cost的更新。
• 最优性的保证：每一个被扩展过的节点的g（n）都能保证是起始节点到当前n节点的最小代价的路径。

上图算法流程中的priority queue即优先级队列，这个队列中的排序方式是通过g（n）也就是cost的大小来进行排序的。

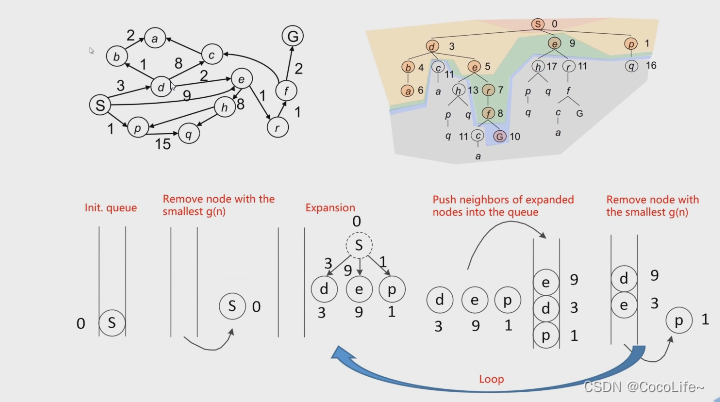
• pros：解是完备的且最优的（如果存在这样的解的话，dijkstra算法一定可以找到并且是最优解）
• cons：找解的时候是全方向均匀扩散的，类似BFS，因为没有终点相关的信息。

A*算法 （Dijkstra with a heuristic）

dijkstra算法的缺点是类似与BFS，没有终点相关的信息，所以是盲目地全向进行搜索的，而上文我们讨论过启发式搜索这样的一个思路，即贪心算法，那是否可以将贪心算法的搜索思路与dijkstra算法具备完备最优解的特性进行结合呢？这个思路也就引出了A算法。
基于以上的思路，A算法的弹出节点的判断方式转换为最小的f（n）=g（n）+h（n），即累计cost和与终点猜测值的和。


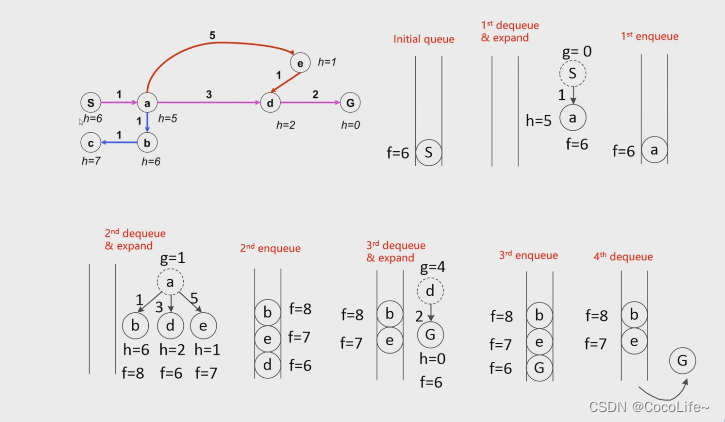
当然，如果不对h（n）这一项进行约束的话，错误的启发式距离的猜测会导致整个算法出问题，如下图中情况，

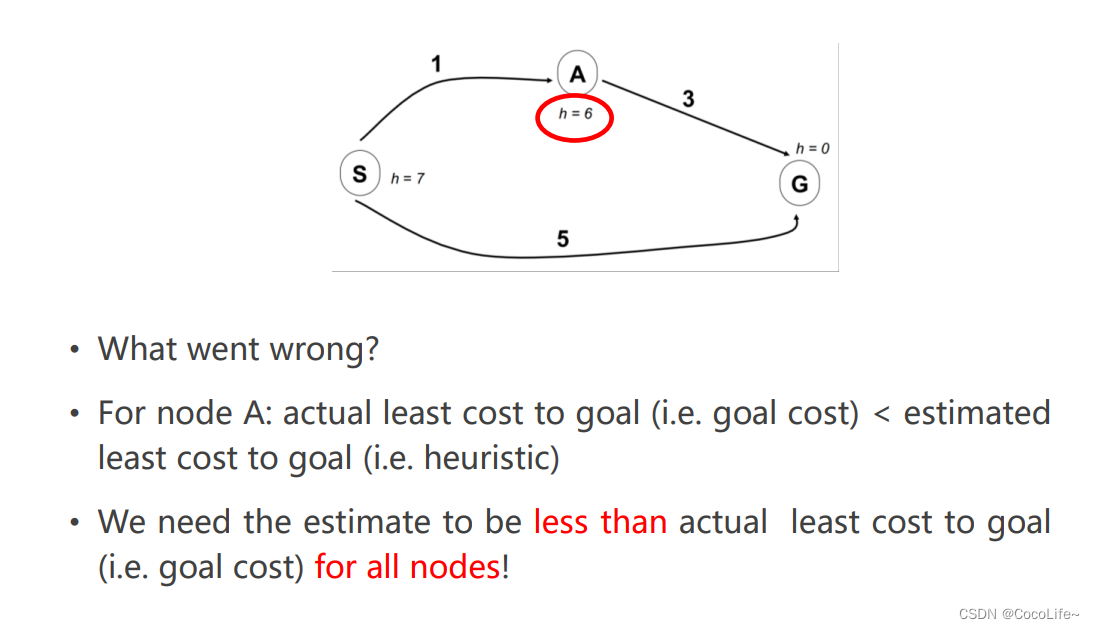
在这张图中，从上面路径走的话，在A节点的f（n）=1+6=7，在下面路径走的话，f（n）=5+0=5，显然，优先级队列会先弹出下方S->G的路径，而G是终点，整个程序就结束了，但是从图中很明显可以看到，上方S->A->G这条路径的cost总和是较小的，因此这种情况下并没有走最优解的路径。
因此，为了保证A*算法的最优性，需要保证每个节点估计出来的h（n）是小于其真实到达最终点的路径长度h的。

A*算法启发式函数的讨论

上文在分析时，为了保证A*算法严格具有最优性，需要保证**每个节点估计出来的h（n）是小于其真实到达最终点的路径长度h的。**那什么样的启发式函数的选择可以保证最优性呢，看下图：

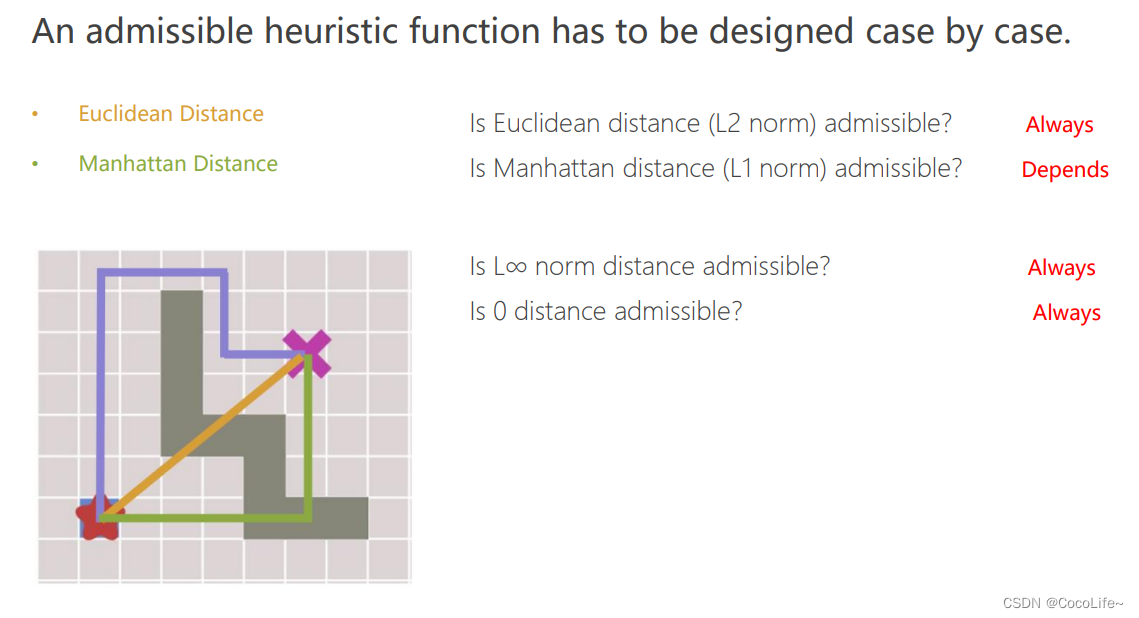
A算法变体-weighted A算法

上面都是在讲怎么保证严格有最优性，那如果就是不要最优性，牺牲最优性会带来什么呢？
答案是算法计算速度的提升。也就是weighted A*所采用的方式，排序依赖的函数变为f = g + εh, ε > 1，ε越大，整个算法越向贪心算法靠拢，ε越小整个算法越向Dijkstra算法靠拢。
cost（次优solution）<= εcost（optimal solution）
对以上方法感兴趣的可以通过路径搜索演示

A*算法在工程上实用的trick

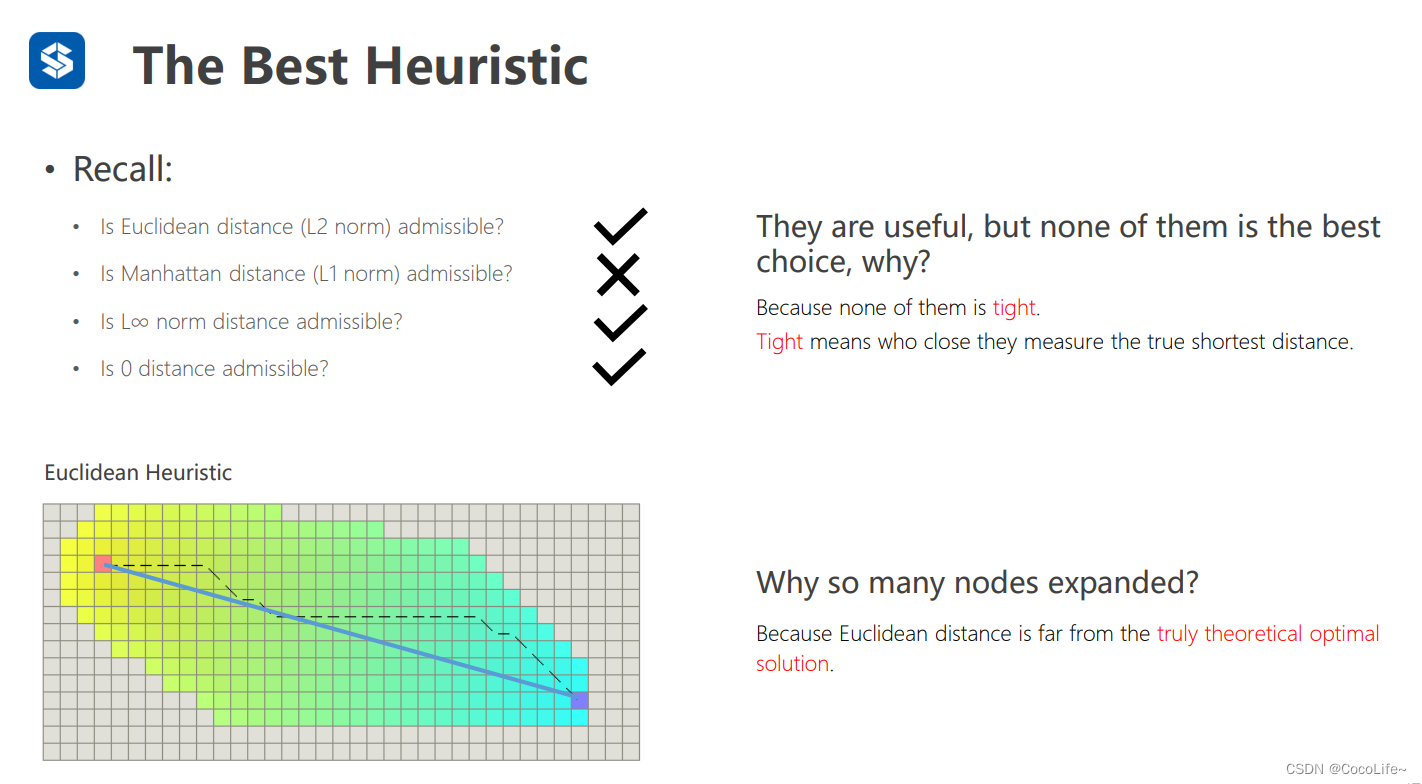
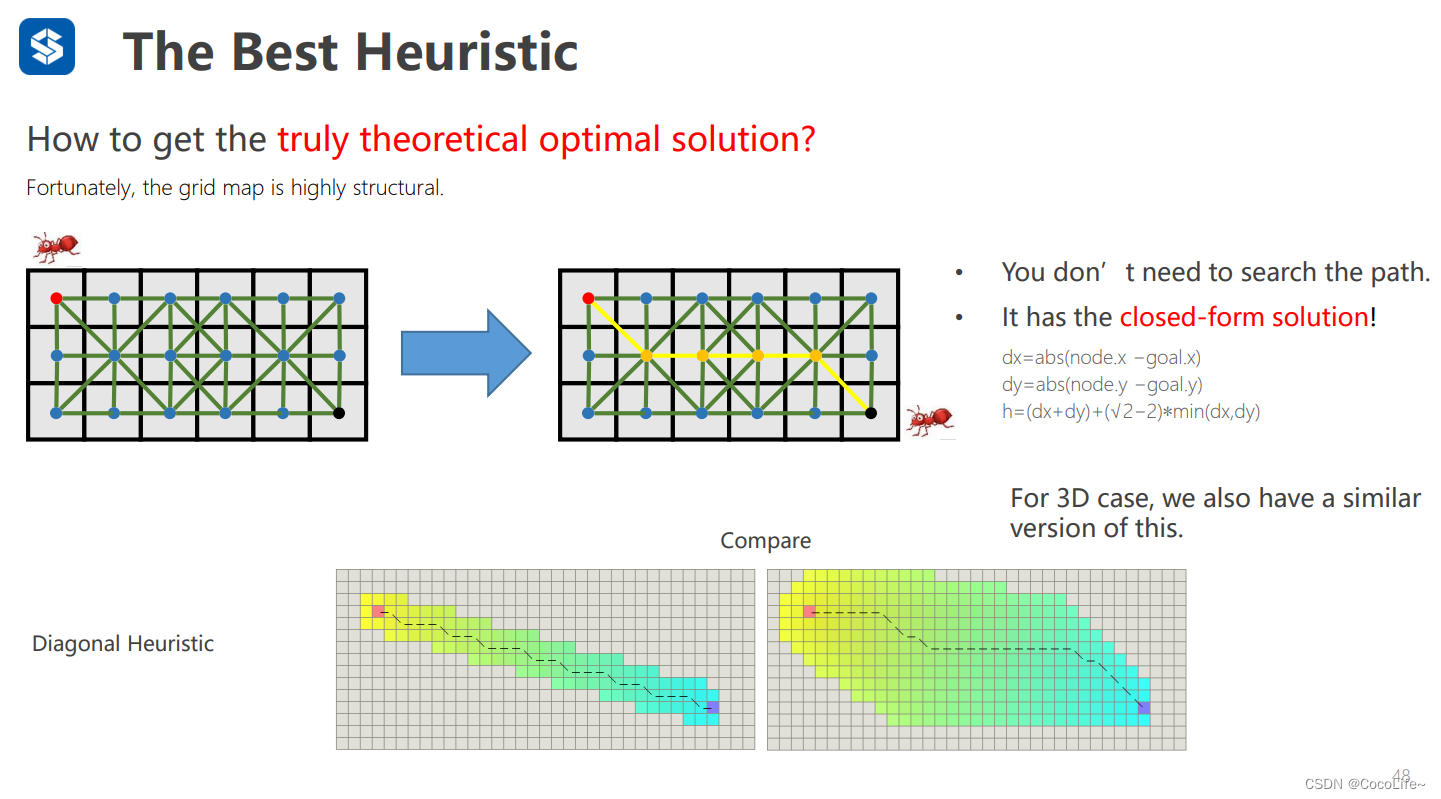
以上的几个启发式函数都不是最好的，因为他们虽然都比较小保证了最优性，但是他们并不是贴紧真实h的，导致了搜索的时候会走很多无用的格子，这个时候可用如下的对角启发式函数来找到最接近真实的h，从而减少无用的探索。

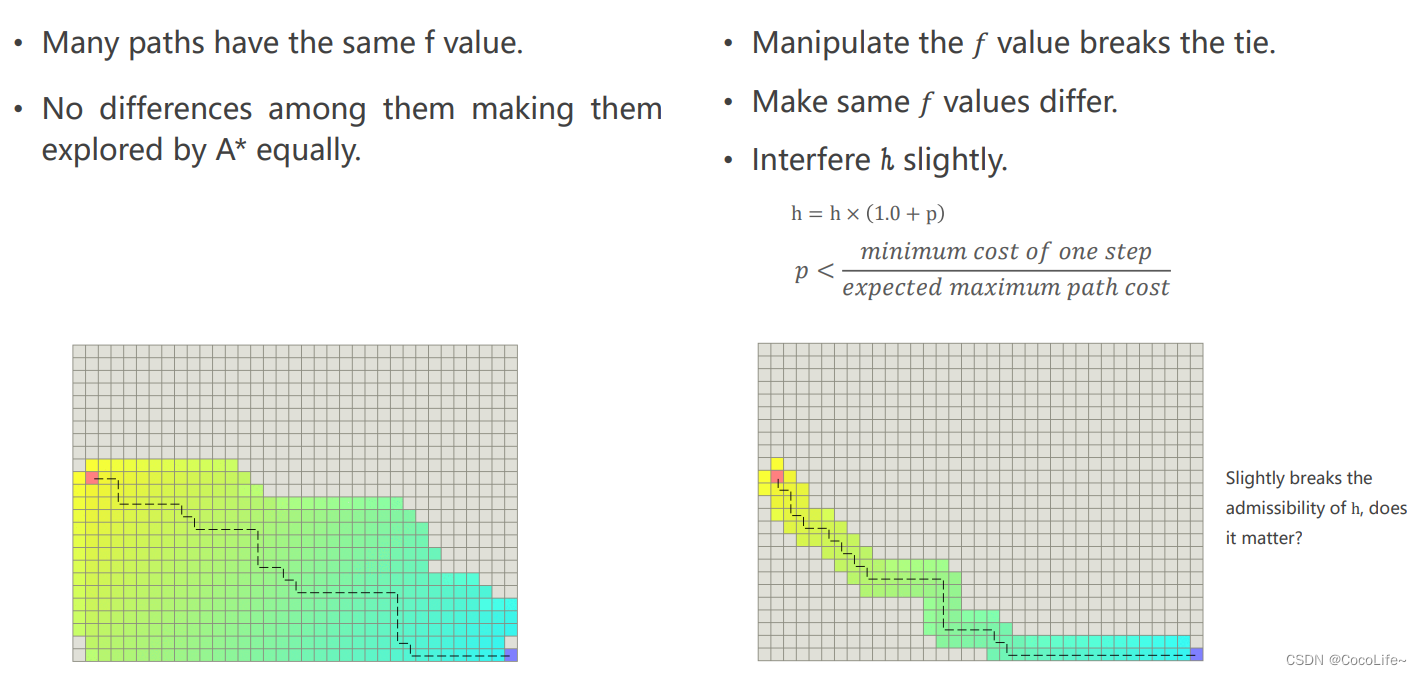
另外一个trick是微调h去影响经过计算具有同样f的两个节点，这样也可以让算法缩小探索的范围，如下图所示，引入一个系数p（一般非常小），一步最小的cost与期待最长的cost的比值，这样会让本来有着相同f的两个节点产生细微差别，从而让模型更具备倾向性。
然而，很直观地可以想到，这样会不会破坏admissible的条件，理论上是会的，但是工程中因为有障碍物的存在，启发式函数算出来的估测值往往小于真实路径的长度。

同样tie breaker（打破对称性）的方式还有：

• 对同样的f的节点，再根据其h进行排序
• 对每一个节点加上一个随机的数值（事先确定好每一个坐标不一样，根据坐标构建哈希表）
• 添加选节点的倾向性（可以人为设定）

Jump Point Search

系统性彻底消除对称性路径的方法。
其核心idea就是找到路径中的对称性，并且打破它。

• look ahead rule：根据父节点来的方向以及障碍物存在的位置，智能判断哪些节点需要扩展哪些不需要扩展
  
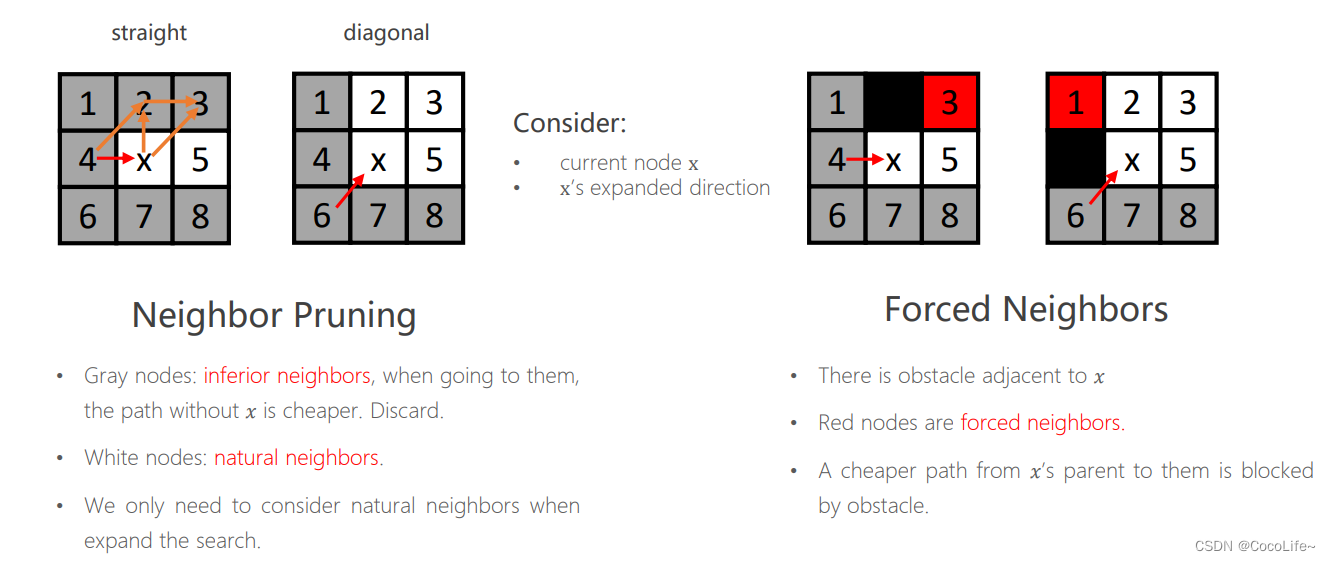
  比如上图左侧的九宫格中，灰色的叫做劣性节点，放弃扩展，因为这些节点“从父节点出发走到该节点的路径会小于等于（straight情况是小于等于、diagonal情况是小于）经过x再到该节点走的路径的长度”，因此就没有必要从父节点经过x节点再到这些劣性节点的位置。特别地，如果存在障碍物，如上图右侧的九宫格中的黑色格子，某些节点（红色，强迫邻居）会因为障碍物变为也需要考虑扩展的节点。
• Jumping rule：其实就是递归地执行上述的look ahead rule，在各个“跳跃点”之间的节点被忽略，跳跃点的判定：
  ①如果点 y 是起点或目标点，则 y 是跳点
  ②如果 y 有邻居且是强迫邻居则 y 是跳点，从上文强迫邻居的定义来看 neighbor 是强迫邻居，current 是跳点，二者的关系是伴生的，-
  ③如果 parent到 y 是对角线移动，并且 y 经过水平或垂直方向移动可以到达跳点，则 y 是跳点。（不会出现折线跳跃）
  
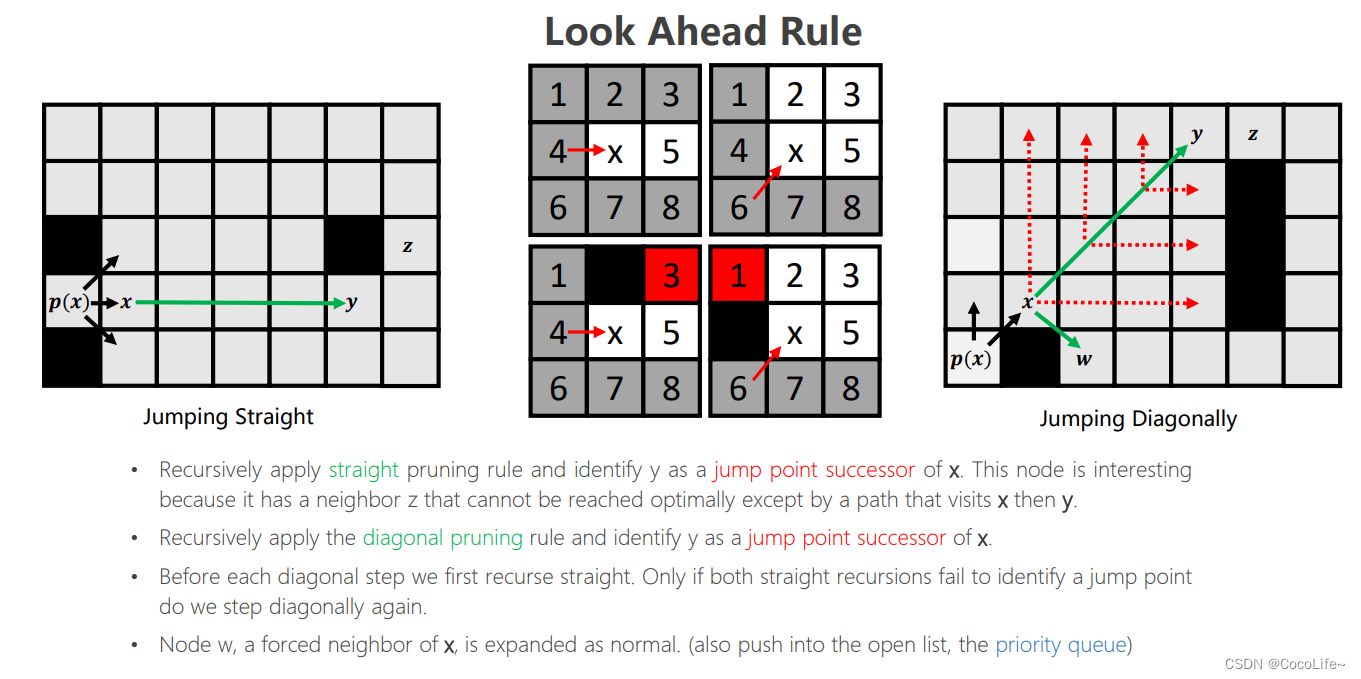
  注意对每一个节点判断时一定是先straight在diagonal，straight如果撞到边界或墙之前没有跳点的话就转而去diagonal jump，如上图最右侧的地图中，从出发点出发，找到x后，出发点弹出，x是第一个跳点，因为有w这个强制邻居（w也是跳点），而后y是跳点（父节点对角线移动到y，y可以水平移动到z，z有强制邻居）。至此，x被弹出，进入close list。
  
  
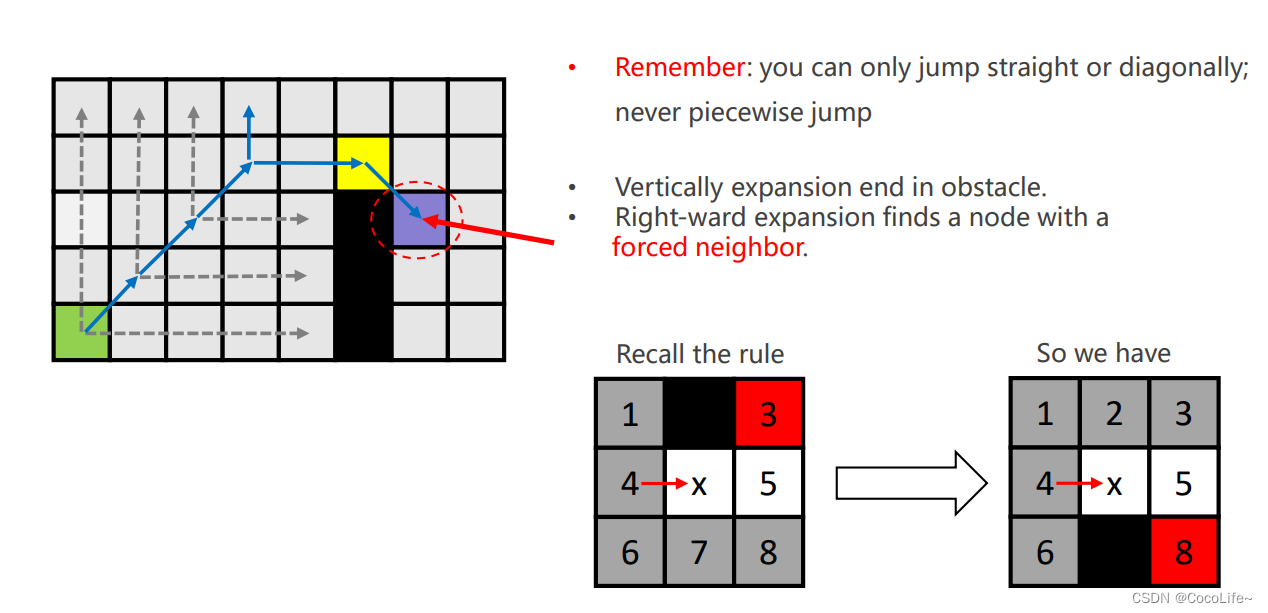
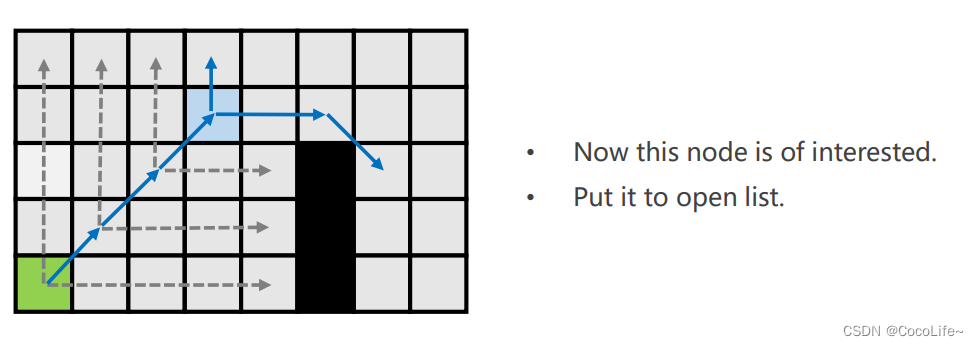
  上方例子，绿色是出发点，沿对角线到蓝色格子，蓝色格子经过水平跳跃后可以到特殊点，所以蓝色格子是跳点，放入open list，绿色点弹出，进入close list。下面是完整的探索过程，所有带颜色的格子都是加入openlist的节点
  

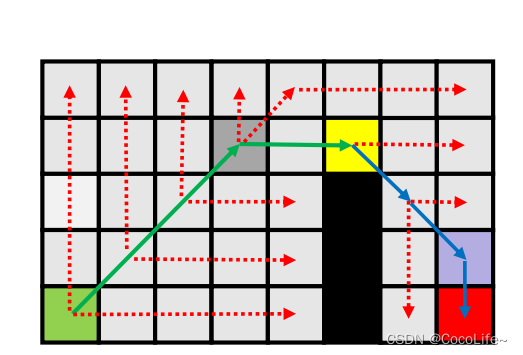
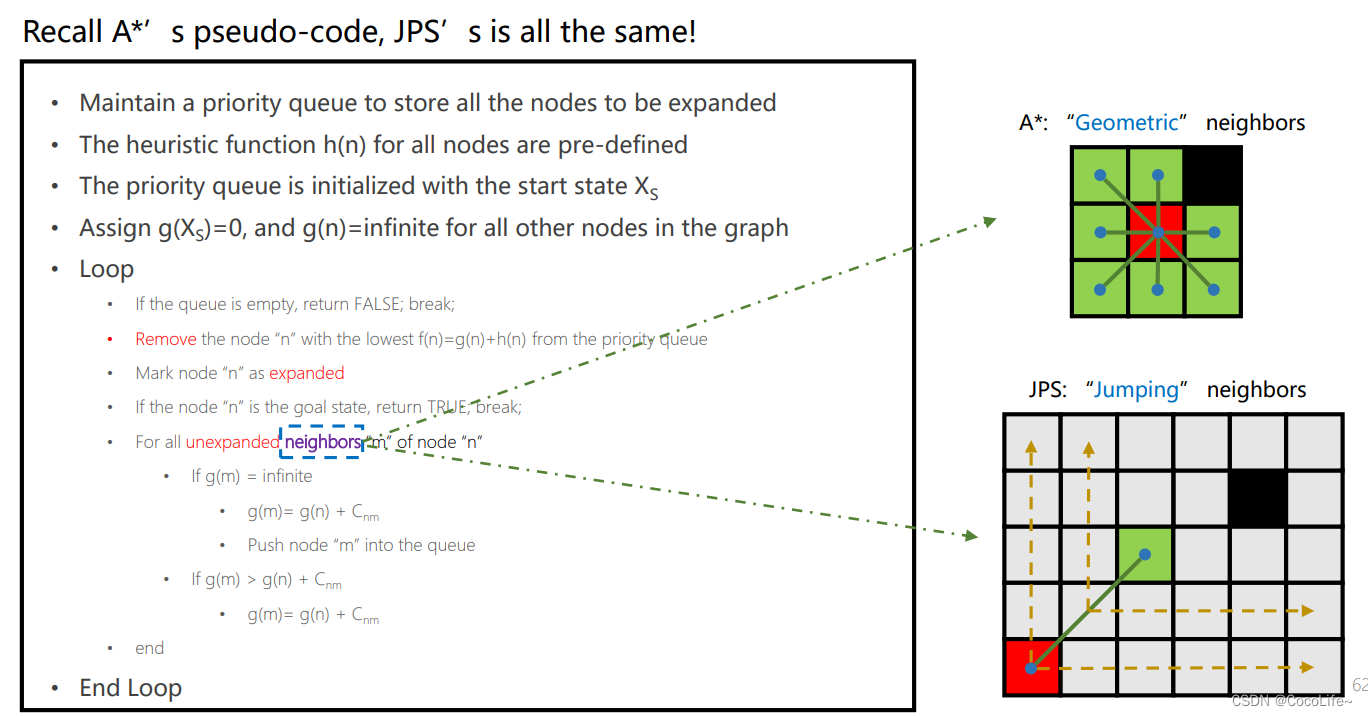
写出来其实和A一样，只不过A找的是几何上的邻居，JPS找的是刚才所讲到的后继跳点。
3D的推广参考论文，原理是一样的，只是进行维度上的扩展，感兴趣的可以去看看源代码

Planning Dynamically Feasible Trajectories for Quadrotors using Safe Flight Corridors in 3-D Complex Environments, Sikang Liu, RAL 2017

JPS算法的缺陷

一般在正常情况下，JPS都会比A要高效一些，因为它省略了两个跳点之间的很多点，不必加入open list。但是，在如下图所示的，很大的地图中很少的障碍物的情况，JPS甚至会比A满很多倍，原因在于，先进行水平、垂直的跳点搜索时，每一个都要判断撞到障碍物或者边界才结束（额外引入status query/collision quert，一般情况较小，比较空旷的场景则有可能很多），而边界又很远。
而且JPS只能用于uniform grid map，也就是这里图所示的这种地图，对于更广义的图来讲，A*是可以的，但是JPS就不行了。

本章作业后续会在同系列更新：）