scikit-learn

1. 优缺点

在大家的日常生活中，无论是工作还是学习，scikit-learn都占有举足轻重的地位！先聊聊它的优缺点，让大家有一个整体的认识！

1.1. 优点

• 简单易用：scikit-learn提供了一种简单而一致的API，使用户能够轻松地训练、评估和部署各种监督学习模型。
• 丰富的文档和示例：详尽的文档和示例，以帮助用户理解算法和如何使用它们，这降低了学习曲线。
• 广泛的算法支持：包括多种监督学习算法，从传统的线性模型到集成方法和深度学习，满足了各种问题的需求。
• 开源社区支持：强大的开源社区，用户可以获得支持、反馈和贡献新功能和改进。
• 性能优化：库中的算法通常经过高度优化，以提供高性能的计算，特别是在大规模数据集上。
• 数据预处理工具：包括数据预处理、特征工程和特征选择工具，有助于准备和处理数据。
• 交叉验证和模型选择：提供了交叉验证和模型选择工具，有助于选择最佳模型参数，避免过拟合。
• 可扩展性：用户可以轻松地扩展库，自定义评估器、转换器和度量。

1.2. 缺点

• 有些算法的性能：尽管scikit-learn包括广泛的算法，但某些特殊问题可能需要更专业的库或深度学习框架来实现最佳性能。
• 深度学习支持限制：虽然scikit-learn包括MLP（多层感知机）等神经网络模型，但对于深度学习任务，深度学习框架如TensorFlow和PyTorch可能更适合。
• 自动特征工程：自动特征工程工具有限，复杂的特征工程任务可能需要其他库或手动处理。
• 处理大规模数据集的能力：对于大规模数据集，scikit-learn的性能和内存管理可能存在挑战。
• 不支持序列数据：对于时序数据或自然语言处理任务，需要额外的库和工具。

有了一个整体的认识之后，专门针对监督学习算法，各个举例，给出大家完整可以抛出结果的代码示例来。

2. 监督学习

线性模型

线性与二次判别分析

核脊回归

支持向量机

随机梯度下降

最近邻

高斯过程

横向分解

朴素贝叶斯

决策树

组合：梯度增强，随机森林，装袋，投票，堆叠

多类与多输出算法

特征选择

半监督学习

等张回归

概率标定

神经网络模型（监督）

2.1. 线性回归

线性回归案例中，包括准备数据、构建模型、训练模型、预测、评估和可视化。

• 导入所需的库，包括NumPy、Matplotlib以及Scikit-Learn的相关模块。
• 加载波士顿房价数据集，选择平均房间数作为特征（这里仅选取了一个特征用于简化示例）。
• 划分数据集为训练集和测试集，这是为了评估模型的性能。
• 创建并训练线性回归模型，使用训练数据进行拟合。
• 使用模型进行预测，预测测试集中的房屋价格。
• 评估模型性能，计算均方误差（MSE）和决定系数（R^2）。
• 最后，通过可视化，绘制了实际数据点和线性回归模型的拟合线，以便直观地了解模型的性能。

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 加载波士顿房价数据集
boston = datasets.load_boston()

# 准备数据
X = boston.data[:, np.newaxis, 5]  # 选取房间数作为特征
y = boston.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 构建线性回归模型
model = LinearRegression()

# 训练模型
model.fit(X_train, y_train)

# 进行预测
y_pred = model.predict(X_test)

# 评估模型
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 可视化结果
plt.scatter(X_test, y_test, color='black', label='实际数据')
plt.plot(X_test, y_pred, color='blue', linewidth=3, label='线性回归拟合')
plt.title('线性回归预测房价')
plt.xlabel('平均房间数')
plt.ylabel('房屋价格')
plt.legend()
plt.show()

print(f"均方误差(Mean Squared Error): {mse:.2f}")
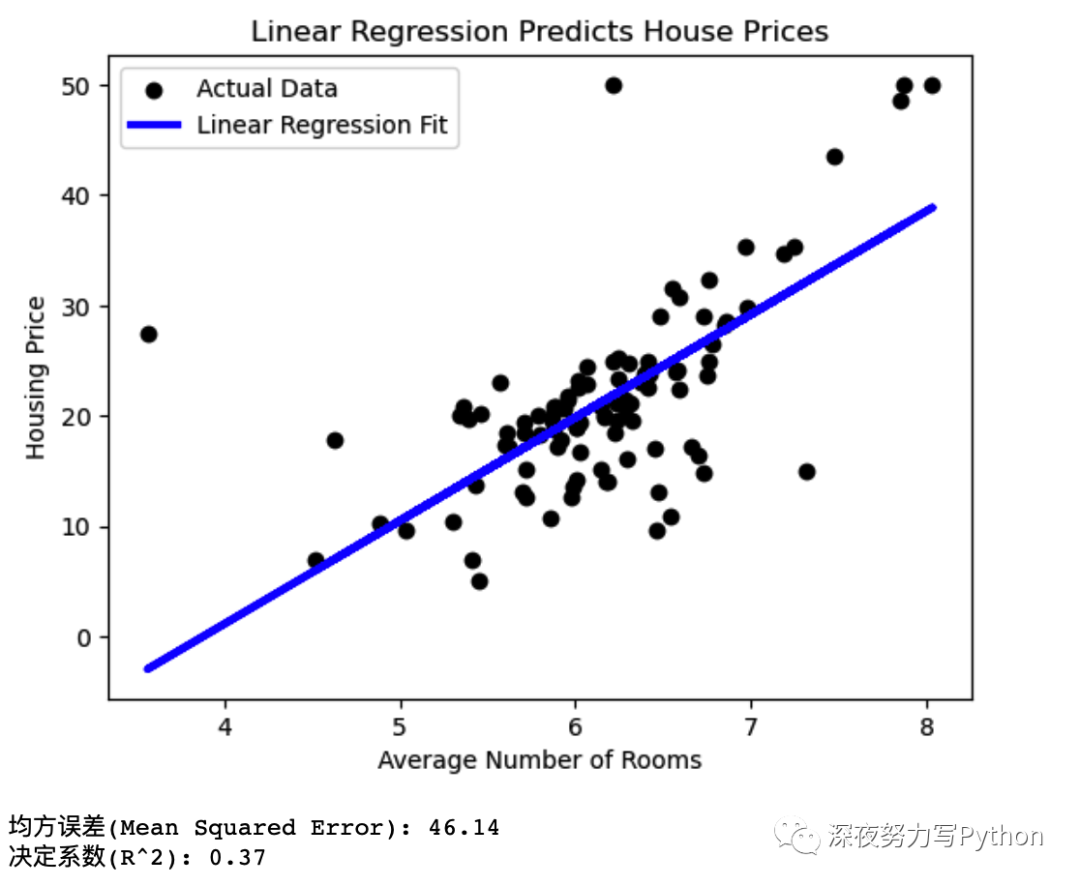
print(f"决定系数(R^2): {r2:.2f}")

线性回归的本质问题是通过最小化实际值和预测值之间的误差来找到一条最佳拟合线，以预测目标变量。

在这个示例中，咱们使用房间数来预测房屋价格，然后通过图形展示了线性回归的拟合效果。

2.2. 逻辑回归

咱们使用Scikit-Learn中的Iris数据集，该数据集包含了三个不同种类的鸢尾花的测量数据，我们将使用逻辑回归来预测其中两个种类之一。

• 导入 NumPy、Matplotlib以及Scikit-Learn的相关模块。
• 加载Iris数据集，选择两个特征（萼片长度和萼片宽度）以便于可视化。将标签转换为二进制分类问题，其中0表示一种鸢尾花，1表示另一种鸢尾花。
• 创建并训练逻辑回归模型。
• 使用模型绘制决策边界图，这个图显示了逻辑回归的分类边界以及数据点的分布。

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import LogisticRegression

# 加载Iris数据集
iris = datasets.load_iris()
X = iris.data[:, :2]  # 仅使用前两个特征，便于可视化
y = (iris.target != 0) * 1  # 将标签转换为二进制分类问题

# 构建逻辑回归模型
model = LogisticRegression(solver='liblinear')

# 训练模型
model.fit(X, y)

# 绘制决策边界图
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k')
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('LogisticRegression')
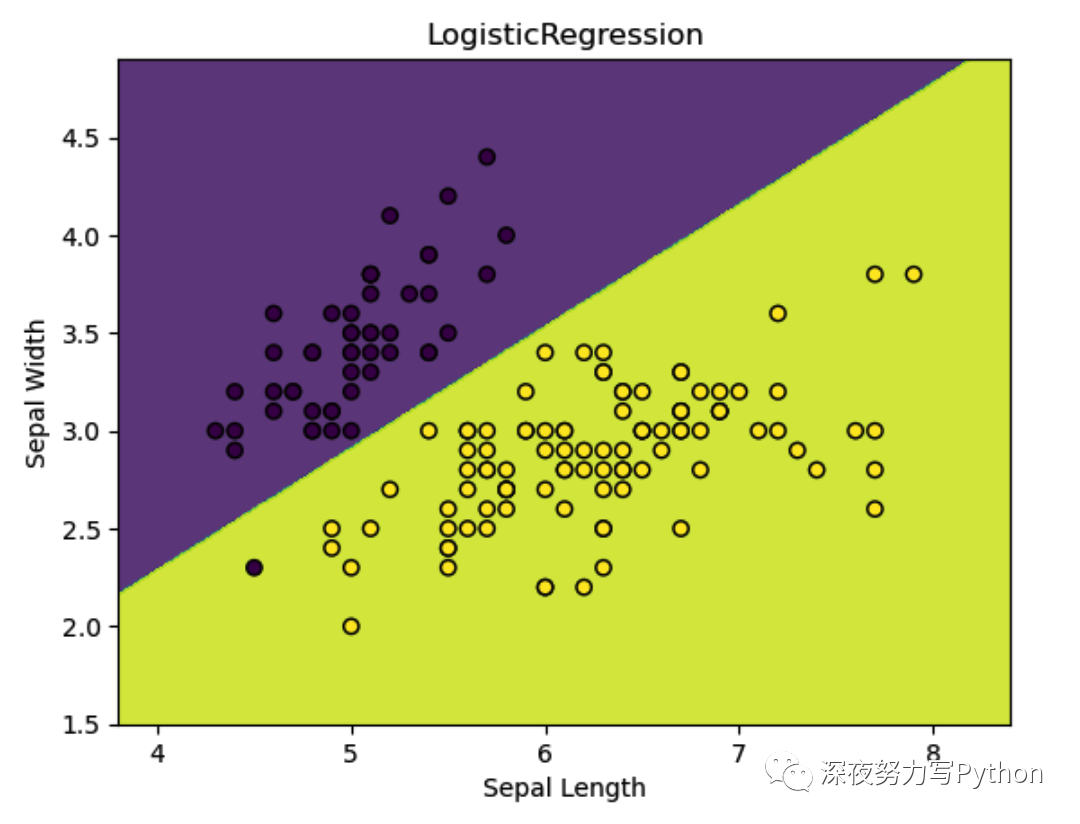
plt.show()

逻辑回归的本质问题是通过找到一个决策边界，将数据点分为两个类别。

示例中，逻辑回归模型找到了一条分隔两种鸢尾花的决策边界。这个图像也展示了逻辑回归如何用于二元分类问题的关键概念。

2.3. 支持向量机

下面案例使用 Scikit-Learn 的SVM模型进行新颖性检测，包括准备数据、构建模型、完整代码以及可视化说明支持向量机的本质问题。

案例中，咱们使用一个具有正常观测和异常观测的合成数据集。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm

# 生成一个合成数据集
np.random.seed(0)
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))

# 构建支持向量机模型
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
clf.fit(X_train)

# 预测结果
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)

# 统计预测错误数量
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

# 绘制图像
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.title("Novelty Detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors="darkred")
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors="palevioletred")

s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c="white", s=s, edgecolors="k")
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c="blueviolet", s=s, edgecolors="k")
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c="gold", s=s, edgecolors="k")
plt.axis("tight")
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend(
    [a.collections[0], b1, b2, c],
    [
        "Learned Frontier",
        "Training Observations",
        "New Regular Observations",
        "New Abnormal Observations",
    ],
    loc="upper left",
    prop=plt.matplotlib.font_manager.FontProperties(size=11),
)
plt.xlabel(
    "Train Errors: %d/200 ; Novel Regular Errors: %d/40 ; Novel Abnormal Errors: %d/40"
    % (n_error_train, n_error_test, n_error_outliers)
)
plt.show()

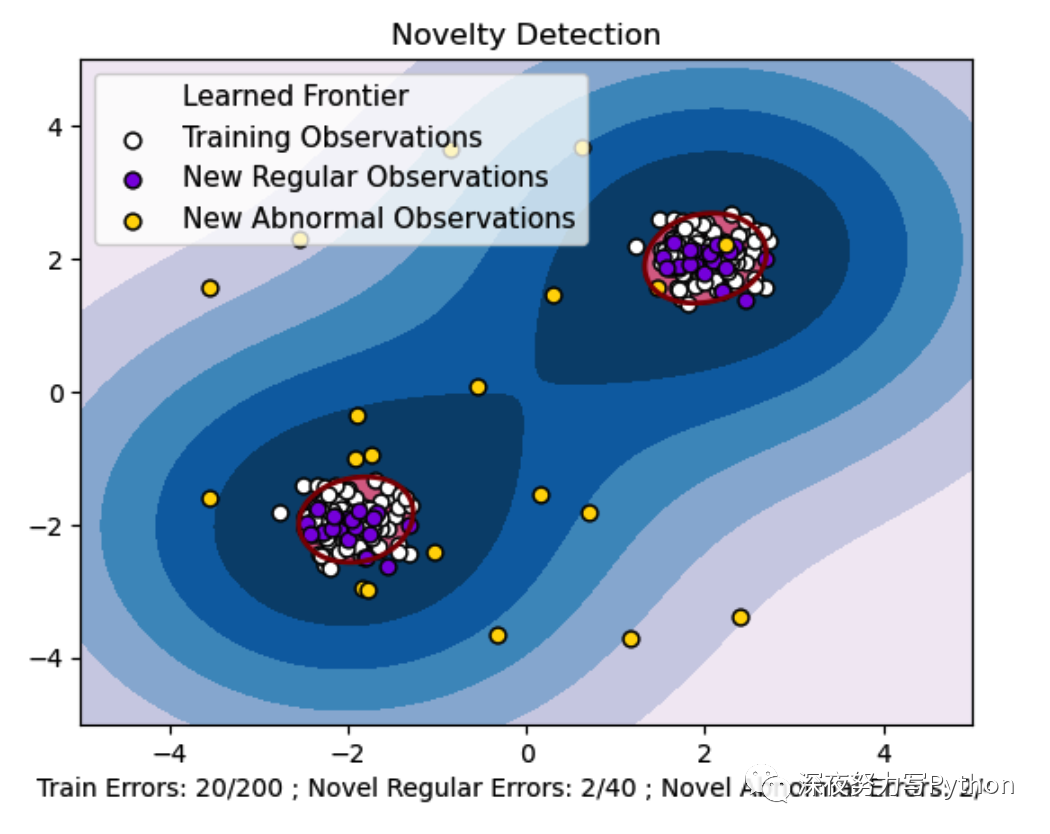
示例中，咱们创建了一个合成数据集，包括正常观测和异常观测。

然后，我们使用One-Class SVM模型进行新颖性检测，找到决策边界，将正常观测和异常观测分开。

通过可视化，我们可以看到支持向量机是如何找到一个学习边界，将正常观测与异常观测分开的。

演示了支持向量机在异常检测问题中的应用。

2.3. 决策树和随机森林

在下面案例中，咱们使用Scikit-Learn的Iris数据集，并训练决策树和随机森林模型以可视化它们的决策边界。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier

# 加载Iris数据集
iris = load_iris()

# Parameters
n_classes = 3
plot_colors = "ryb"
plot_step = 0.02

# 创建一个包含2x2子图的图形
fig, sub = plt.subplots(2, 2)
plt.subplots_adjust(wspace=0.4, hspace=0.4)

# 为不同的特征组合训练和绘制决策树和随机森林的决策边界
for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3], [1, 2]]):
    X = iris.data[:, pair]
    y = iris.target

    # 训练决策树模型
    clf_tree = DecisionTreeClassifier().fit(X, y)

    # 训练随机森林模型
    clf_rf = RandomForestClassifier(n_estimators=100, random_state=42).fit(X, y)

    # 绘制决策边界
    ax = sub[pairidx // 2, pairidx % 2]
    DecisionBoundaryDisplay.from_estimator(
        clf_tree,
        X,
        cmap=plt.cm.RdYlBu,
        response_method="predict",
        ax=ax,
        xlabel=iris.feature_names[pair[0]],
        ylabel=iris.feature_names[pair[1]],
    )
    ax.set_title("Decision Tree")

    DecisionBoundaryDisplay.from_estimator(
        clf_rf,
        X,
        cmap=plt.cm.RdYlBu,
        response_method="predict",
        ax=ax,
        xlabel=iris.feature_names[pair[0]],
        ylabel=iris.feature_names[pair[1]],
    )
    ax.set_title("Random Forest")

    # 绘制训练点
    for i, color in zip(range(n_classes), plot_colors):
        idx = np.where(y == i)
        ax.scatter(
            X[idx, 0],
            X[idx, 1],
            c=color,
            label=iris.target_names[i],
            cmap=plt.cm.RdYlBu,
            edgecolor="black",
            s=15,
        )

# 添加标题和图例
plt.suptitle("Decision Surface of Decision Trees and Random Forest on Pairs of Features")
plt.legend(loc="lower right", borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()

这段代码执行以下步骤：

• 加载Iris数据集，其中包含了花的特征和类别。
• 对于每个不同的特征组合，训练一个决策树模型和一个随机森林模型。
• 使用DecisionBoundaryDisplay可视化模型的决策边界。
• 绘制训练数据点，用不同颜色表示不同的类别。

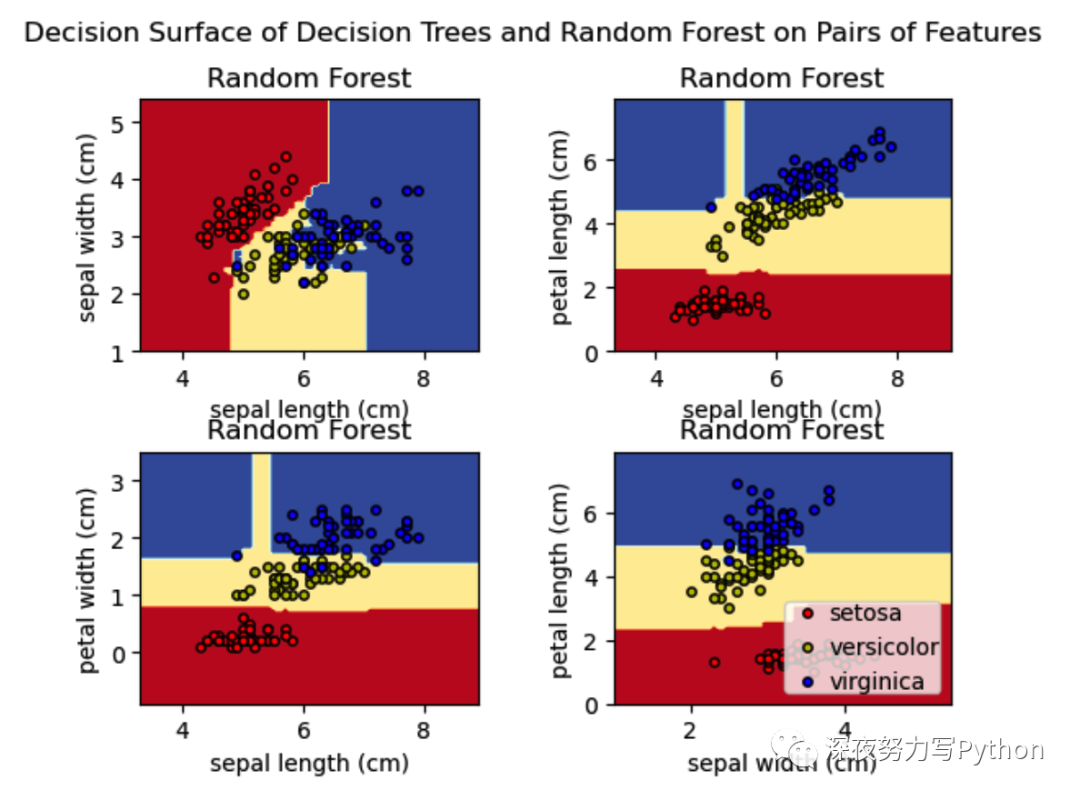
这个图像展示了决策树和随机森林的决策边界，以及它们如何在Iris数据集的不同特征组合下进行分类。这有助于理解这两种模型的本质问题，以及它们如何根据不同特征组合进行分类。

3. 无监督学习

高斯混合模型

流形学习

聚类

双聚类

信号的分量分解(矩阵分解问题)

协方差估计

新颖性与离群点检测

密度估计

神经网络（无监督）

3.1. K-Means

下面案例中，咱们使用Scikit-Learn生成合成数据并应用K-Means聚类。

• 使用make_blobs函数生成一个合成数据集，包括1000个数据点，每个数据点有2个特征，共有4个簇。
• 创建K-Means模型，并指定要分成4个簇。
• 使用生成的数据训练K-Means模型。
• 获取聚类的中心和每个数据点的标签。
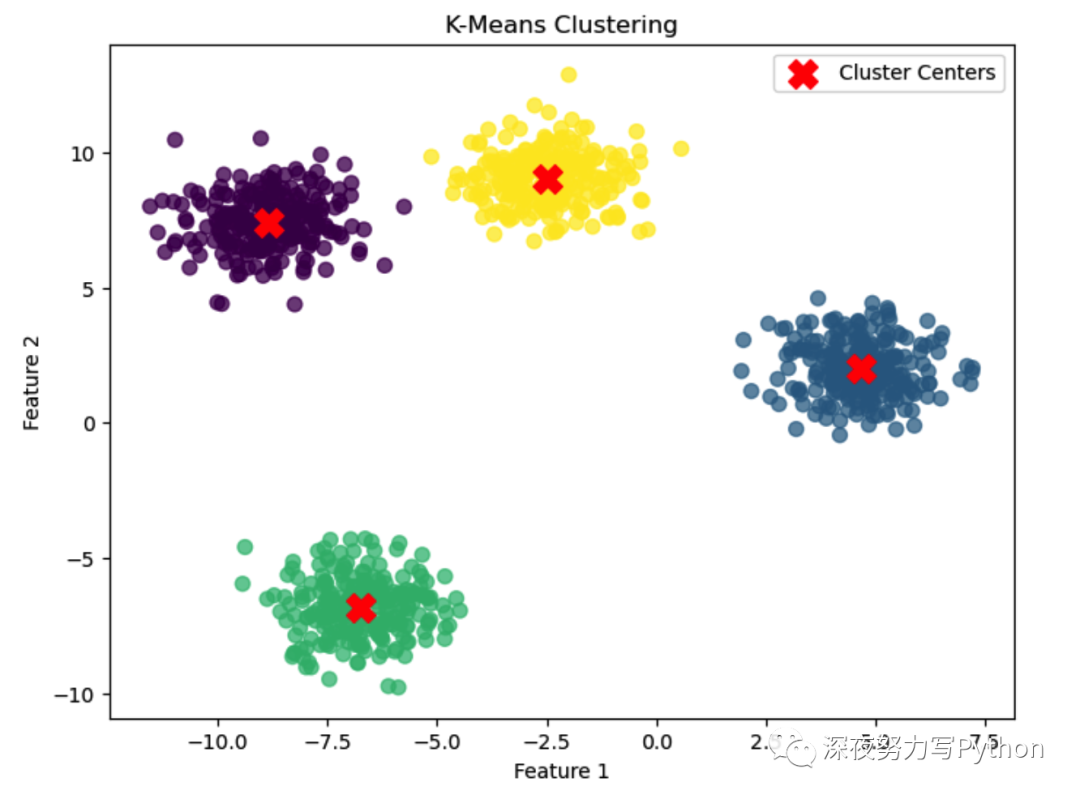
• 绘制数据点，并用不同颜色表示不同的簇，同时用红色的"X"表示簇中心。

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成合成数据
n_samples = 1000
n_features = 2
n_clusters = 4
random_state = 42

X, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=random_state)

# 构建K-Means模型
kmeans = KMeans(n_clusters=n_clusters, random_state=random_state)

# 训练模型
kmeans.fit(X)

# 获取簇中心和预测标签
cluster_centers = kmeans.cluster_centers_
labels = kmeans.labels_

# 绘制数据点和簇中心
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, alpha=0.7)
plt.scatter(cluster_centers[:, 0], cluster_centers[:, 1], c='red', s=200, marker='X', label='Cluster Centers')
plt.title('K-Means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()

这个图像展示了K-Means聚类的本质问题，即将数据点分成不同的簇，以便更好地理解数据的结构。

3.2. 集成方法

集成方法案例中，咱们使用Scikit-Learn创建一个合成数据集。

并分别使用RandomTreesEmbedding和ExtraTreesClassifier构建集成方法模型。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
from sklearn.decomposition import TruncatedSVD
from sklearn.ensemble import ExtraTreesClassifier, RandomTreesEmbedding
from sklearn.naive_bayes import BernoulliNB

# 创建一个合成数据集
X, y = make_circles(factor=0.5, random_state=0, noise=0.05)

# 使用RandomTreesEmbedding来转换数据
hasher = RandomTreesEmbedding(n_estimators=10, random_state=0, max_depth=3)
X_transformed = hasher.fit_transform(X)

# 使用TruncatedSVD降维以可视化
svd = TruncatedSVD(n_components=2)
X_reduced = svd.fit_transform(X_transformed)

# 使用BernoulliNB学习一个朴素贝叶斯分类器
nb = BernoulliNB()
nb.fit(X_transformed, y)

# 使用ExtraTreesClassifier进行比较
trees = ExtraTreesClassifier(max_depth=3, n_estimators=10, random_state=0)
trees.fit(X, y)

# 绘制图表
fig = plt.figure(figsize=(9, 8))

ax = plt.subplot(221)
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_title("Original Data (2d)")
ax.set_xticks(())
ax.set_yticks(())

ax = plt.subplot(222)
ax.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y, s=50, edgecolor="k")
ax.set_title(
    "Truncated SVD reduction (2d) of transformed data (%dd)" % X_transformed.shape[1]
)
ax.set_xticks(())
ax.set_yticks(())

# 在原始空间中绘制决策边界
h = 0.01
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# 使用RandomTreesEmbedding来转换网格
transformed_grid = hasher.transform(np.c_[xx.ravel(), yy.ravel()])
y_grid_pred = nb.predict_proba(transformed_grid)[:, 1]

ax = plt.subplot(223)
ax.set_title("Naive Bayes on Transformed data")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1,], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

# 使用ExtraTreesClassifier进行预测
y_grid_pred = trees.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

ax = plt.subplot(224)
ax.set_title("ExtraTrees predictions")
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor="k")
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

plt.tight_layout()
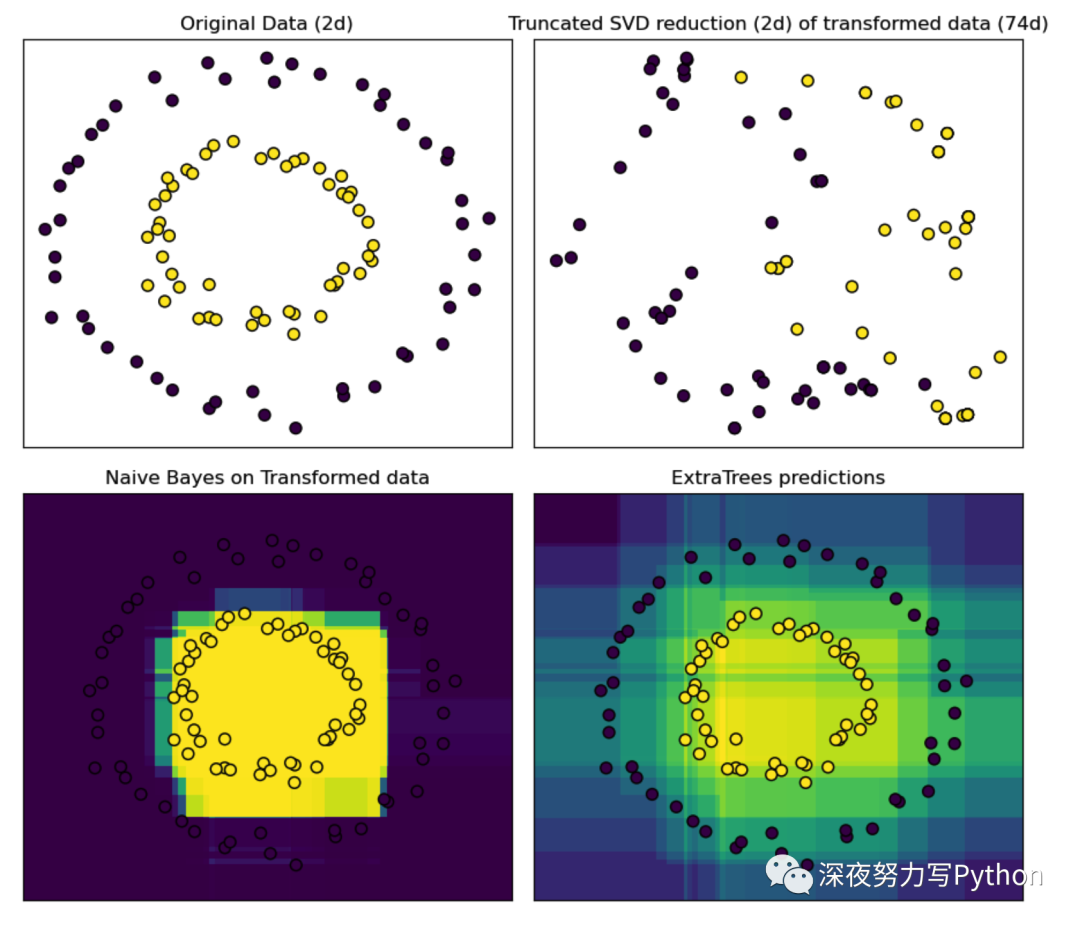
plt.show()

这个案例演示了使用集成方法中的RandomTreesEmbedding和ExtraTreesClassifier对合成数据集进行处理，以及如何可视化决策边界和分类效果。

这有助于理解集成方法的本质问题，以及如何通过组合多个模型来提高性能。

3.3. 高斯混合模型

高斯混合模型（Gaussian Mixture Model，GMM）是一种用于聚类和密度估计的概率模型。它假设数据是由多个高斯分布混合而成的，每个高斯分布表示一个聚类。这个例子中，我们将使用Sklearn中的GaussianMixture类来演示如何构建和可视化GMM模型。

这个案例中，咱们依然使用Sklearn的内置数据集Iris，该数据集包含了三种不同种类的鸢尾花的特征测量。尝试使用GMM来对这些数据进行聚类。

准备数据： 我们将使用Sklearn内置的Iris数据集，该数据集包含了鸢尾花的四个特征测量：花萼长度（sepal length）、花萼宽度（sepal width）、花瓣长度（petal length）和花瓣宽度（petal width）。

构建模型： 我们将使用GMM模型来聚类数据。GMM模型的核心思想是假设数据是由多个高斯分布组成的混合模型。模型会自动估计每个分布的参数，包括均值和协方差矩阵。

完整代码：

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.mixture import GaussianMixture
from sklearn.decomposition import PCA

# 加载Iris数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 创建GMM模型
n_components = 3  # 聚类数量，这里选择3类
gmm = GaussianMixture(n_components=n_components)

# 拟合模型
gmm.fit(X)

# 预测每个样本的聚类标签
labels = gmm.predict(X)

# 获取每个样本属于每个聚类的概率
probs = gmm.predict_proba(X)

# 降维可视化
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)

# 绘制聚类结果
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=labels, cmap='viridis')
plt.title('GMM Clustering')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')

plt.subplot(1, 2, 2)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=probs, cmap='viridis', marker='x')
plt.title('GMM Clustering (Probabilities)')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')

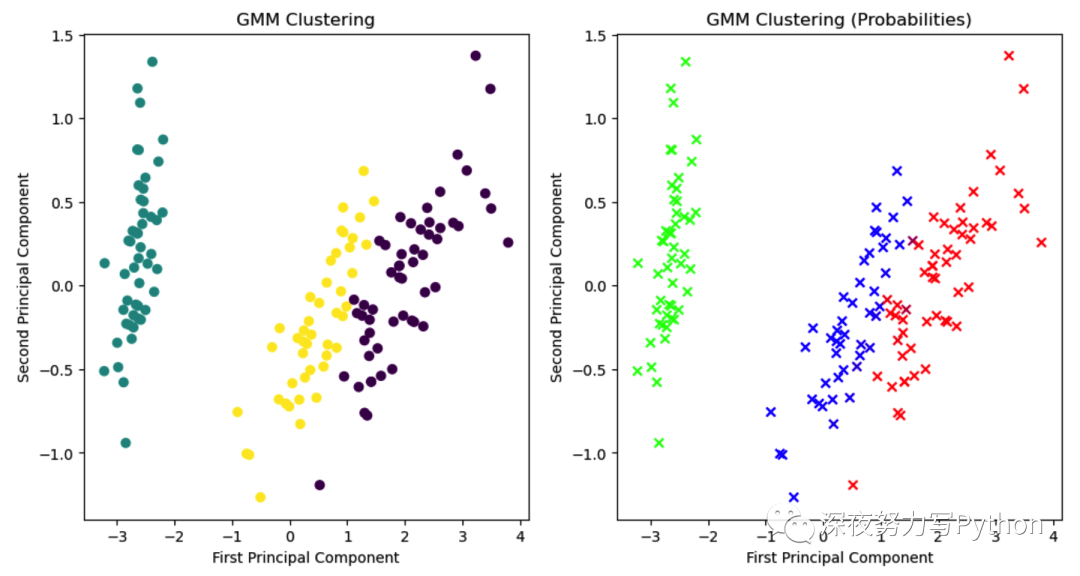
plt.show()

上面代码中，咱们首先加载了Iris数据集，然后创建了一个GMM模型并拟合数据。

使用PCA将数据降维到二维空间以便可视化。然后，我们绘制了两幅图像，左边的图像显示了GMM的聚类结果，右边的图像显示了每个样本属于每个聚类的概率。

这个案例演示了如何使用GMM来对数据进行聚类，并展示了GMM的聚类效果和概率分布。GMM是一种强大的聚类算法，特别适用于数据具有多个不同的分布的情况。

3.4. 梯度提升树

梯度提升树（Gradient Boosting）通过迭代地训练多个决策树来不断改进模型的性能。使用Scikit-Learn中的GradientBoostingClassifier来说明如何使用梯度提升树来解决分类问题。

例子中，使用Scikit-Learn中的三个不同数据集来演示梯度提升树的应用。这些数据集包括Iris数据集、一个分类数据集和Hastie数据集。分别对这些数据集应用梯度提升树模型，并比较它们的性能。

准备数据： 我们将使用Scikit-Learn内置的数据集，包括Iris数据集、一个分类数据集和Hastie数据集。这些数据集都包含特征和标签。

构建模型： 我们将使用GradientBoostingClassifier来构建梯度提升树模型。该模型会迭代地训练多个决策树，以最小化损失函数，从而提高分类性能。

完整代码：

import time
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, ensemble
from sklearn.model_selection import train_test_split

# 数据集和名称
data_list = [
    datasets.load_iris(return_X_y=True),
    datasets.make_classification(n_samples=800, random_state=0),
    datasets.make_hastie_10_2(n_samples=2000, random_state=0),
]
names = ["Iris Data", "Classification Data", "Hastie Data"]

# 初始化列表用于存储结果
n_gb = []
score_gb = []
time_gb = []
n_gbes = []
score_gbes = []
time_gbes = []

n_estimators = 200

for X, y in data_list:
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.2, random_state=0
    )

    # 创建梯度提升树模型
    gbes = ensemble.GradientBoostingClassifier(
        n_estimators=n_estimators,
        validation_fraction=0.2,
        n_iter_no_change=5,
        tol=0.01,
        random_state=0,
    )
    gb = ensemble.GradientBoostingClassifier(n_estimators=n_estimators, random_state=0)

    # 训练并记录时间
    start = time.time()
    gb.fit(X_train, y_train)
    time_gb.append(time.time() - start)

    start = time.time()
    gbes.fit(X_train, y_train)
    time_gbes.append(time.time() - start)

    # 计算准确度并记录
    score_gb.append(gb.score(X_test, y_test))
    score_gbes.append(gbes.score(X_test, y_test))

    # 记录训练的迭代次数
    n_gb.append(gb.n_estimators_)
    n_gbes.append(gbes.n_estimators_)

# 绘制图形
bar_width = 0.2
n = len(data_list)
index = np.arange(0, n * bar_width, bar_width) * 2.5
index = index[0:n]

plt.figure(figsize=(10, 6))
plt.bar(index, score_gb, bar_width, label='Gradient Boosting', color='b', alpha=0.7)
plt.bar(index + bar_width, score_gbes, bar_width, label='Gradient Boosting with Early Stopping', color='g', alpha=0.7)
plt.xlabel('Dataset')
plt.ylabel('Accuracy')
plt.title('Accuracy of Gradient Boosting vs. Early Stopping Gradient Boosting')
plt.xticks(index + bar_width, names)
plt.legend(loc='best')
plt.tight_layout()
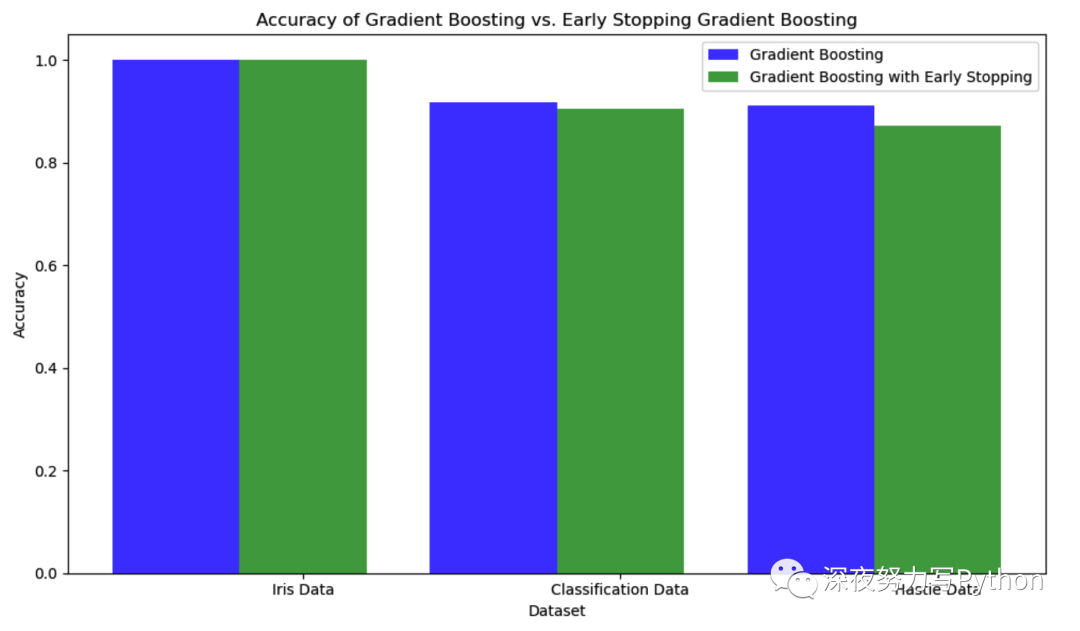
plt.show()

代码中，我们首先加载了三个不同的数据集，然后分别应用了梯度提升树和具有提前停止机制的梯度提升树模型。

记录了训练时间、准确度和迭代次数，并使用Matplotlib绘制了比较图，以展示梯度提升树和提前停止梯度提升树的性能。

上面案例演示如何使用梯度提升树来解决分类问题，并展示了提前停止机制对模型性能的影响。梯度提升树是一种强大的集成学习算法，可用于解决各种分类和回归问题。

3.5. AdaBoost

我们考虑一个简单的回归任务。假设我们有一组数据，它们遵循某种未知的非线性关系，可能受到一些随机噪声的影响。我们的目标是使用AdaBoost回归器对这种关系进行建模，并可视化其预测效果。

使用AdaBoostRegressor来完成这个任务。AdaBoost是一种自适应的学习算法，可以提高弱学习算法的性能。在回归任务中，AdaBoostRegressor工作原理是通过拟合一系列弱学习器（例如决策树）来逐渐纠正之前所有学习器的错误。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor

# 生成模拟数据
rng = np.random.default_rng(42)
X = np.sort(5 * rng.random(80))[:, np.newaxis]
y = np.sin(X).ravel() + rng.normal(0, 0.1, X.shape[0])

# 使用决策树和AdaBoost回归器
regr_1 = DecisionTreeRegressor(max_depth=4)
regr_2 = AdaBoostRegressor(DecisionTreeRegressor(max_depth=4), n_estimators=300, random_state=42)

regr_1.fit(X, y)
regr_2.fit(X, y)

y_1 = regr_1.predict(X)
y_2 = regr_2.predict(X)

# 可视化结果
colors = sns.color_palette("colorblind")
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color=colors[0], label="training samples")
plt.plot(X, y_1, color=colors[1], label="Decision Tree", linewidth=2)
plt.plot(X, y_2, color=colors[2], label="AdaBoost", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree and AdaBoost Regression")
plt.legend()
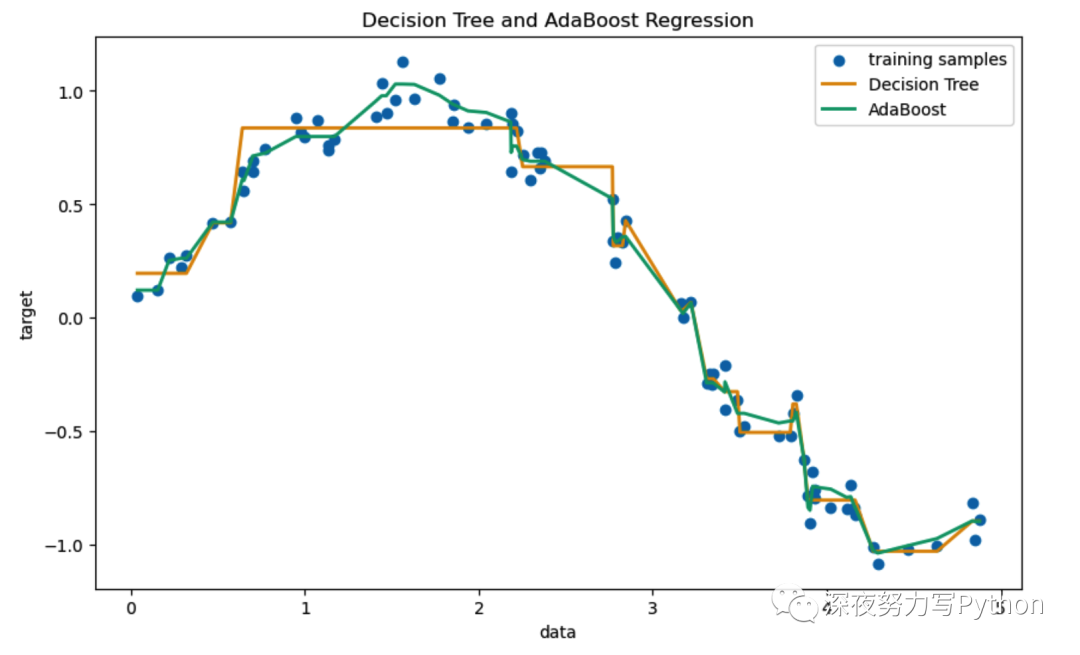
plt.show()

上面首先创建了一个由正弦函数和噪声生成的模拟数据集。然后，我们用普通的决策树和AdaBoost训练了回归模型。最后，我们在图形中对比了这两种方法的预测效果。

从图形中，你会看到AdaBoost能够更好地捕捉数据的非线性趋势，并且对于噪声点也有更好的鲁棒性。

3.6. 神经网络

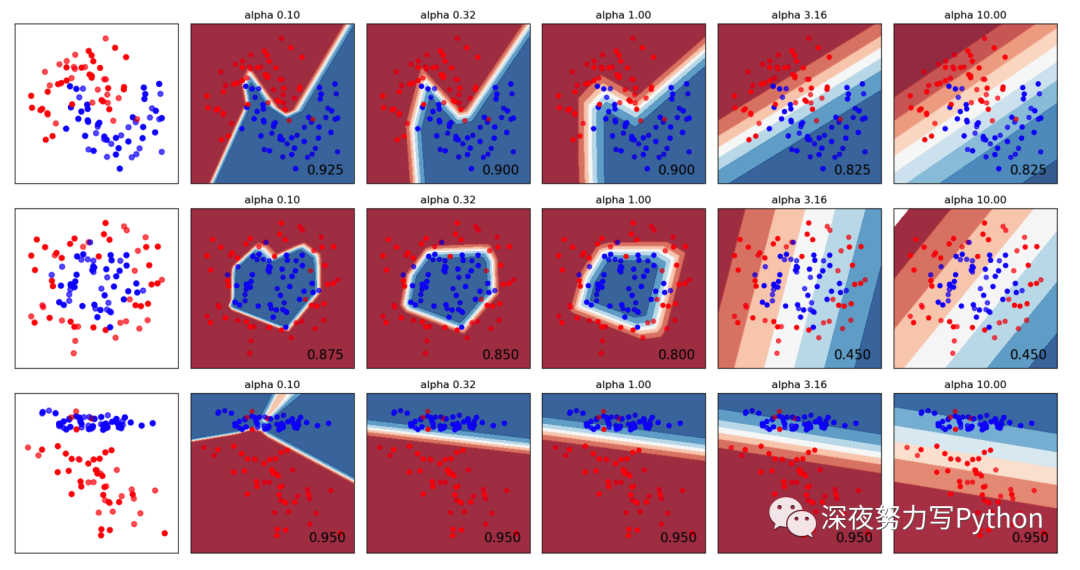
使用神经网络来对几个2D数据集进行分类。具体来说，我们将对三个常用的合成数据集进行分类：月亮、圆和一个线性可分离的数据集。

目标是通过改变正则化参数来展示神经网络的性能，并对其决策边界进行可视化。

数据准备:

• 月亮形数据集（make_moons）: 这个数据集包含两个重叠的半圆形。

• 圆形数据集（make_circles）: 这个数据集包含一个大圈和一个小圈。

• 线性可分离的数据集: 这是一个简单的可分离的数据集，加入了一些噪声。

构建模型:

我们将构建一个两层隐藏层的MLP（多层感知机）分类器，并将正则化参数（alpha）进行变化，从而探索不同正则化强度对模型性能的影响。

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap

from sklearn.datasets import make_circles, make_classification, make_moons
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import StandardScaler

h = 0.02  # step size in the mesh

# 定义不同的alpha值
alphas = np.logspace(-1, 1, 5)

# 为每个alpha值构建一个MLP分类器
classifiers = []
names = []
for alpha in alphas:
    classifiers.append(
        MLPClassifier(
            solver="lbfgs",
            alpha=alpha,
            random_state=1,
            max_iter=2000,
            hidden_layer_sizes=[10, 10]
        )
    )
    names.append(f"alpha {alpha:.2f}")

# 创建数据集
datasets = [
    make_moons(noise=0.3, random_state=0),
    make_circles(noise=0.2, factor=0.5, random_state=1),
    make_classification(n_features=2, n_redundant=0, n_informative=2, random_state=0, n_clusters_per_class=1)
]

# 可视化结果
figure = plt.figure(figsize=(17, 9))
i = 1
# 遍历数据集
for X, y in datasets:
    X = StandardScaler().fit_transform(X)
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)

    x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
    y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    cm = plt.cm.RdBu
    cm_bright = ListedColormap(["#FF0000", "#0000FF"])
    ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
    ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
    ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    ax.set_xticks(())
    ax.set_yticks(())
    i += 1

    for name, clf in zip(names, classifiers):
        ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
        clf.fit(X_train, y_train)
        score = clf.score(X_test, y_test)

        if hasattr(clf, "decision_function"):
            Z = clf.decision_function(np.column_stack([xx.ravel(), yy.ravel()]))
        else:
            Z = clf.predict_proba(np.column_stack([xx.ravel(), yy.ravel()]))[:, 1]

        Z = Z.reshape(xx.shape)
        ax.contourf(xx, yy, Z, cmap=cm, alpha=0.8)
        ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright, s=25)
        ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, s=25, alpha=0.6)
        ax.set_xlim(xx.min(), xx.max())
        ax.set_ylim(yy.min(), yy.max())
        ax.set_xticks(())
        ax.set_yticks(())
        ax.set_title(name)
        ax.text(xx.max() - 0.3, yy.min() + 0.3, f"{score:.3f}", size=15, horizontalalignment="right")
        i += 1

plt.tight_layout()
plt.show()

此代码将为每个数据集的每个正则化参数显示决策边界和模型性能。

4. 模型选择与评估

交叉验证：评估评估器的性能

调优估计器的超参数

度量和评分：量化预测的质量

验证曲线：绘制分数来评价模型

参考文献

scikit-learn: machine learning in Python — scikit-learn 1.3.2 documentation

https://www.cnblogs.com/pinard/p/6026343.html