【C语言】Huffman编码解码简单实现

什么是Huffman编码？

当我们传输数据的时候，有一种传输方式叫做二进制传输，也就是把需要传输的数据转化为二进制数传输给对方。

比如我们有一段文字内容“BADCADFEED”要通过网络传输给别人，把这段内容编码为一段二进制数，将编码后的二进制数传输给对方，对方再根据得到的二进制解码为原内容，实现二进制传输。

如果要实现这一过程，我们可以采用这种方法，文字内容中每一个字符都有一个二进制数与之对应，且每一个字符对应的二进制数的长度是一样的。例如，我可以规定： “A”：000，“B”：001，“C”：010，“D”：011，“E”：100，“F”：101。这样我们就可以把文字内容转化为一段二进制数了，转化后的二进制数是“001000011010000011101100100011”，对方接收到这段二进制数后，每一次读取三个二进制数，根据编码表就可以解码为对应的字符，这个过程就实现了。

但是如果一篇文章内容很长，所包含的字符数量非常大，这种方式编码的二进制数会非常庞大。如果规定等长的二进制数长度为5，他能表示的字符数为2^5=32，ASCII码一共有256个字符，2^8=256，也就是每一个字符需要长度为8的二进制数对应，这样带来的内存消耗是非常大的，那有没有别的编码方式可以减少这种消耗呢？

Huffman提出一种新的编码方式，不再规定二进制数长度的统一，而是设计长短不等的编码，这种编码其实是很容易混淆的，给你一段很长的二进制数，你不知道要在那些地方划分解码，所以这种方式必须满足一个前提，任一字符的编码都不是另一个字符的编码前缀，这种编码方式称为前缀编码，也称为Huffman编码。

---

Huffman树

关于Huffman编码我们先来介绍一下Huffman树。

如果我们所需要传输的文本内容不再是“BADCADFEED”，而是由这六个字符组成的某段文字，这六个字符出现的频率分别为A27,B8,C15,D15,E30,F5。

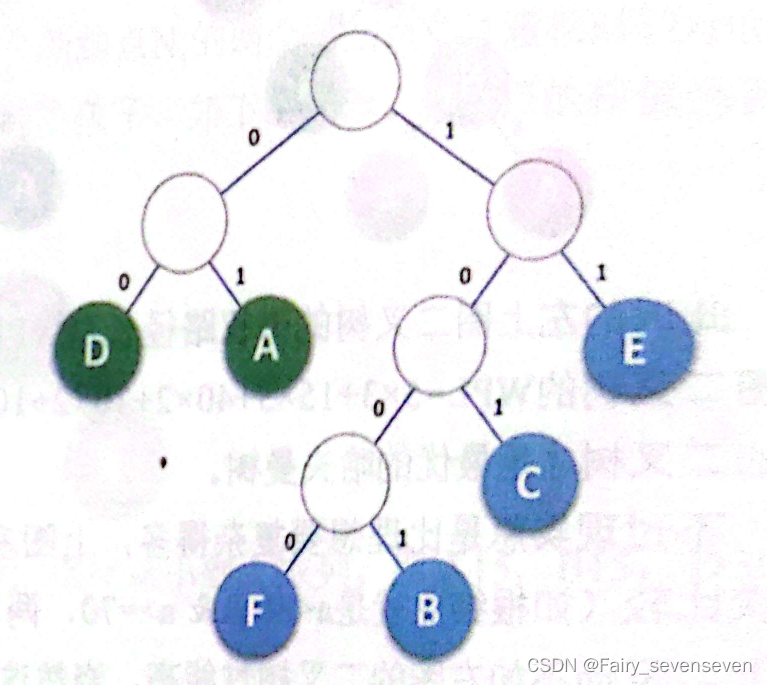
Huffman树 如图所示：

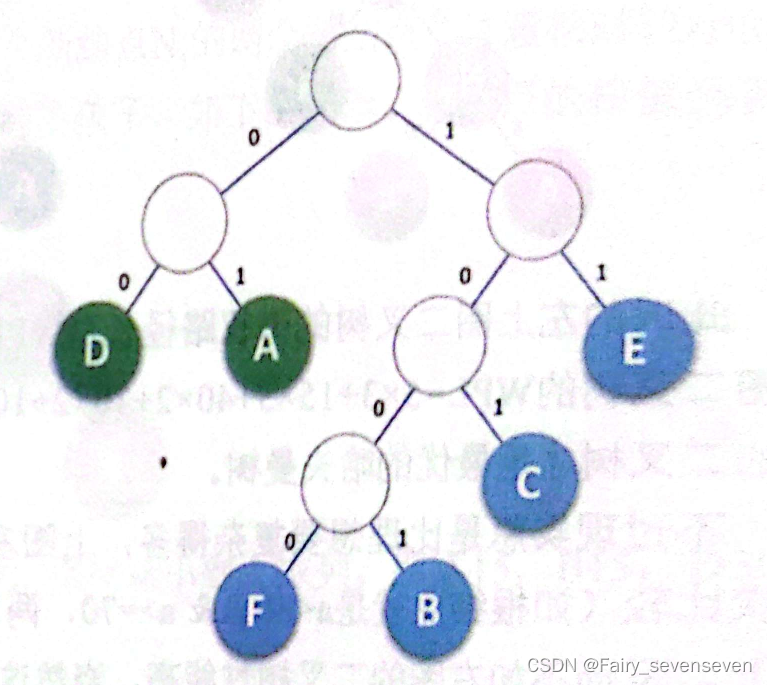
根据Huffman树，我们可以知道，“D”：00，“A”：01，“E”：11，“C”：101，“B”：1001，“F”：1000，从而实现了Huffman编码，设计长短不等的编码，但是就算是长短不一，似乎也不能减少内存的消耗，我们设计等长的二进制数长度是3，Huffman编码所展示的“B”，“F”二进制长度都超过3变为了4，这种编码方式真的可以达到减少消耗的作用吗？可以根据数学计算，计算出此编码方式得到的二进制数总长度与等长度为3的编码方式得到的二进制总长度节省的空间大小，计算公式：二进制数长度减少的个数乘以出现频率减去二进制数长度增加的个数乘以出现频率。

根据公式可以得知，如果可以控制增加长度减少的字符出现频率，减少长度增加的字符出现频率，就可以尽量使得节省空间大小的值更大。根据这个思路，我们把出现频率高的字符安放在离根近的叶子位置，而出现频率低的字符安放在离根远的叶子位置。这就是Huffman编码方式节省空间的原理。

---

 Huffman编码定义

Huffman编码是一种常用的数据压缩算法，通过使用不等长的编码来表示不同的符号，以实现对数据的高效压缩。该算法由David A. Huffman于1952年提出，并且在信息论和压缩领域广泛应用。

Huffman编码的基本思想是，出现频率高的符号使用较短的编码，而出现频率低的符号使用较长的编码。这样可以确保整体的编码长度较短，从而实现数据的高效压缩。

以下是Huffman编码的基本步骤：

1. 统计符号的频率：遍历待压缩的数据，统计每个符号（通常是字符）的出现频率。

2. 构建Huffman树：将每个符号及其频率作为一个节点，构建一个最小堆（Min Heap）或优先队列。不断合并两个具有最小频率的节点，直到只剩下一个节点，即树的根节点。这个树就是Huffman树。

3. 分配编码：从根节点开始，向左走为0，向右走为1，从而得到每个符号的Huffman编码。编码的长度取决于符号在Huffman树中的深度。

4. 构建Huffman编码表：将每个符号及其对应的Huffman编码存储在一个表中，以便进行编码和解码。

5. 数据编码：用Huffman编码表将原始数据中的每个符号替换为相应的Huffman编码，得到压缩后的数据。

Huffman编码的解码过程是编码过程的逆过程：

1. 读取Huffman编码表。
2. 从根节点开始，根据编码的每一位向左或向右遍历Huffman树。
3. 当到达叶子节点时，输出对应的符号，并回到根节点，继续解码下一个编码。

Huffman编码在图像、音频、文本等数据的压缩中得到了广泛应用，因为它能够根据数据的统计特性实现高效的压缩。

---

怎么样构建Huffman树？

前面我们提到了，Huffman树构建思路需要把出现频率高的字符安放在离根结点近的叶子位置，而出现频率低的字符安放在离根结点远的叶子位置。以下是Huffman树构建步骤：

如果我们所需要传输的文本内容不再是“BADCADFEED”，而是由这六个字符组成的某段文字，这六个字符出现的频率分别为A27,B8,C15,D15,E30,F5。

1. 先把这些叶子结点按照从小到大的顺序排列成一个有序序列，即F5,B8,C15,D15,A27,E30。
2. 取头两个出现次数最小的结点作为一个新结点N1的两个子节点，新结点的出现次数算作两个结点出现次数之和。
3. 用N1结点替换F与B，插入有序序列中，保持从小到大排序。即N1 13,C15,D15,A27,E30。
4. 重复步骤2。将N1与C作为一个新结点N2的两个子结点。
5. 将N2替换N1与B，插入有序序列中，保持从小到大排序，即N2 28，D15，A27,E30。
6. 重复步骤2。将N2与D作为一个新结点N3的两个子结点。
7. 将N3替换N2与D，插入有序序列中，保持从小到大排序，即N3 43，A27,E30。
8. 重复步骤2。将N3与A作为一个新结点N4的两个子结点。
9. 将N4替换N3与A，插入有序序列中，保持从小到大排序，即N4 70,E30。
10. 重复步骤2。将N4与E作为一个新结点N5的两个子结点。
11. 将N5替换N4与E，插入有序序列中，保持从小到大排序，即N5100。

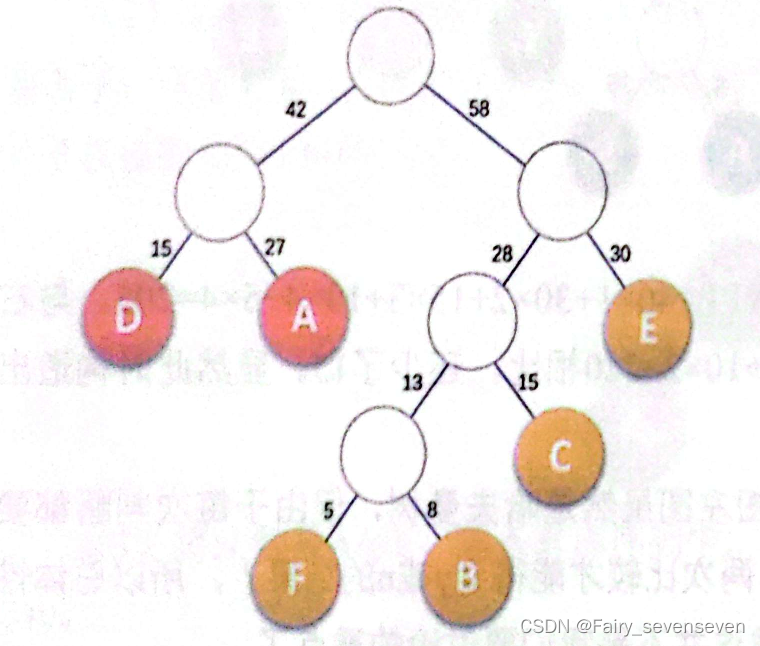
最后得到的Huffman树就如图所示：

---

代码的具体实现

编写结构体

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct Node {
	char data;
	int frequency;
	struct Node* left;
	struct Node* right;
} Node;

 首先我们编写好头文件和Huffman树结点的结构体，结构体中需要存储表示的字符和这个字符的出现频率，以及左孩子和右孩子。

---

 编写创建Huffman结点的函数

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct Node {
	char data;
	int frequency;
	struct Node* left;
	struct Node* right;
} Node;

Node* createNode(char data, int frequency) {
	Node* node = (Node*)malloc(sizeof(Node));
	node->data = data;
	node->frequency = frequency;
	node->left = NULL;
	node->right = NULL;
	return node;
}

 编写一个创建新结点的函数，返回值是结构体指针类型，传入的数据是结构体的字符和字符的出现频率，这样我们直接调用函数就可以得到一个新的结点地址，为接下来的工作做准备。

---

 编写Huffman树构建函数

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct Node {
	char data;
	int frequency;
	struct Node* left;
	struct Node* right;
} Node;

Node* createNode(char data, int frequency) {
	Node* node = (Node*)malloc(sizeof(Node));
	node->data = data;
	node->frequency = frequency;
	node->left = NULL;
	node->right = NULL;
	return node;
}

Node* buildHuffmanTree(char* inputText) {
	int charCount[256] = { 0 };
	int length = strlen(inputText);
	int i;
	
	for (i = 0; i < length; i++) {
		charCount[(int)inputText[i]]++;
	}
	
	Node* nodes[256];
	int nodeCount = 0;
	for (i = 0; i < 256; i++) {
		if (charCount[i] > 0) {
			nodes[nodeCount] = createNode((char)i, charCount[i]);
			nodeCount++;
		}
	}
	
	while (nodeCount > 1) {
		int minFrequency1 = length + 1;
		int minFrequency2 = length + 1;
		int index1 = -1;
		int index2 = -1;
		for (i = 0; i < nodeCount; i++) {
			if (nodes[i]->frequency < minFrequency1) {
				minFrequency2 = minFrequency1;
				index2 = index1;
				minFrequency1 = nodes[i]->frequency;
				index1 = i;
			} else if (nodes[i]->frequency < minFrequency2) {
				minFrequency2 = nodes[i]->frequency;
				index2 = i;
			}
		}
		
		Node* parent = createNode('\0', nodes[index1]->frequency + nodes[index2]->frequency);
		parent->left = nodes[index1];
		parent->right = nodes[index2];
		
		nodes[index2] = parent;
		nodes[index1] = nodes[nodeCount - 1];
		nodeCount--;
	}
	
	return nodes[0];
}

---

 统计符号的频率

int charCount[256] = { 0 };
	int length = strlen(inputText);
	int i;
	
	for (i = 0; i < length; i++) {
		charCount[(int)inputText[i]]++;
	}

 首先我们创建一个charCount数组，空间大小是256，分别对应256个字符，用来计算每一个字符的出现频率，初始化为0。用length变量接收传入的字符串的长度，遍历传入字符串中每一个字符，修正charCount数组，把每一个字符出现频率记录上。

---

 创建叶子结点数组

	Node* nodes[256];
	int nodeCount = 0;
	for (i = 0; i < 256; i++) {
		if (charCount[i] > 0) {
			nodes[nodeCount] = createNode((char)i, charCount[i]);
			nodeCount++;
		}
	}

 接下来我们创建一个结构体数组，用来存放每一个叶子结点，每一个结点对应一个字符，所以空间大小是256，用尾插的方式依次把叶子结点插入nodes数组中。遍历charCount数组，如果数组中字符出现频率大于0，就创建这个字符对应的结构体，尾插进nodes数组中。 

---

 依次合并叶子结点

while (nodeCount > 1) {
		int minFrequency1 = length + 1;
		int minFrequency2 = length + 1;
		int index1 = -1;
		int index2 = -1;
		for (i = 0; i < nodeCount; i++) {
			if (nodes[i]->frequency < minFrequency1) {
				minFrequency2 = minFrequency1;
				index2 = index1;
				minFrequency1 = nodes[i]->frequency;
				index1 = i;
			} else if (nodes[i]->frequency < minFrequency2) {
				minFrequency2 = nodes[i]->frequency;
				index2 = i;
			}
		}
		
		Node* parent = createNode('\0', nodes[index1]->frequency + nodes[index2]->frequency);
		parent->left = nodes[index1];
		parent->right = nodes[index2];
		
		nodes[index2] = parent;
		nodes[index1] = nodes[nodeCount - 1];
		nodeCount--;
	}

 nodeCount是nodes数组中元素的个数，当元素个数大于1就一直合并结点。

首先我们要找到出现频率最小的两个结点，然后合并，用minFrequency1和minFrequency2变量记录频率最小的两个，初始化为length+1，length是传入字符串的长度，也是一个字符可能出现的最大频率，而length+1是不可能出现的频率数，且所有字符出现的频率数都要小于这个数。

用index1和index2变量记录出现频率最小的两个结点的下标。

用一个for循环变量nodes数组每一个节点，找到最小的两个结点，和对应的下标。

创建parent节点，作为两个结点合并后的结点，所代表的频率用两个子结点频率之和表示，左孩子和右孩子链接上。

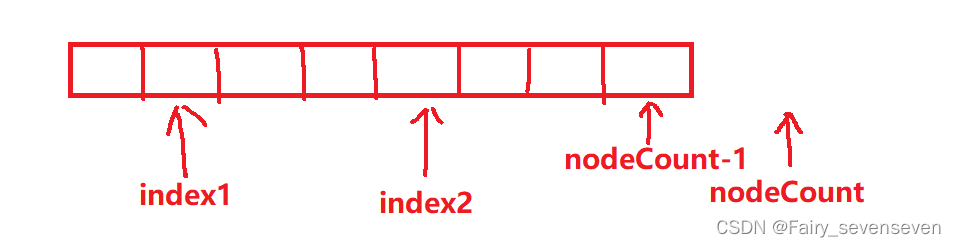
接着把index2上的指针指向parent，index1上的指针指向nodes数组中最后一个元素的地址，nodeCount--，以达到把两个结点合并的效果。至此Huffman树构建函数编写完毕。末尾返回nodes首地址就可以了。

---

 编写Huffman编码表及打印

void printHuffmanCodes(Node* root, int code[], int top, int codeTable[][256], int codeLengths[]) {
	if (root->left) {
		code[top] = 0;
		printHuffmanCodes(root->left, code, top + 1, codeTable, codeLengths);
	}
	if (root->right) {
		code[top] = 1;
		printHuffmanCodes(root->right, code, top + 1, codeTable, codeLengths);
	}
	
	if (root->left == NULL && root->right == NULL) {
		codeLengths[(int)root->data] = top;
		printf("%c:",root->data);
		for (int i = 0; i < top; i++) {
			codeTable[(int)root->data][i] = code[i];
			printf("%d",code[i]);
		}
		printf("\n");
	}
}

 编码表是对于每一个字符，通过这个编码表可以直接找到对应的二进制数。

首先我们得到一个字符的二进制数，是依靠Huffman树选取左右孩子走路走出来的，选左边就是0，右边就是1，一直走到叶子为止。

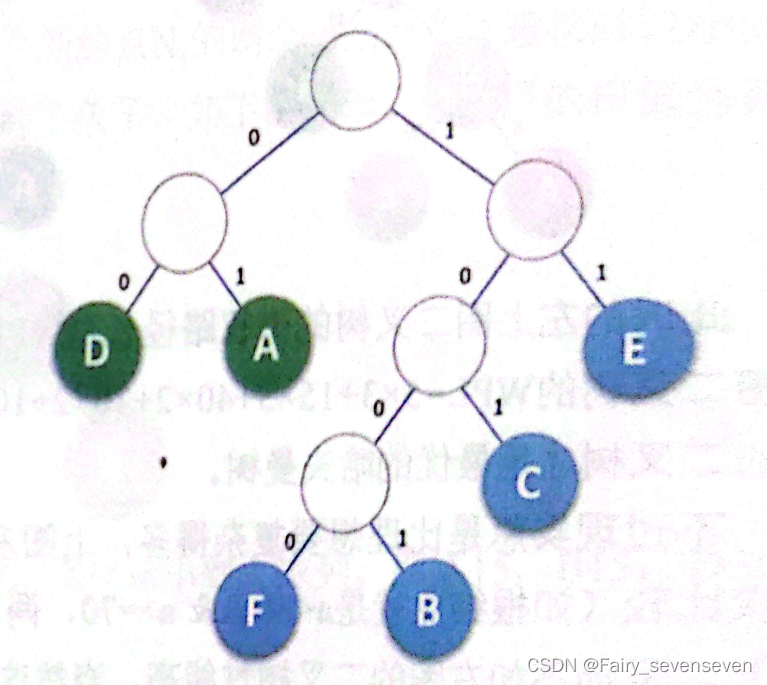
回顾一下，D：00,A:01,E:11,C:101,B:1001,F:1000

所以我们需要遍历Huffman树，利用后序遍历的方式遍历树，对于每一个结点先遍历完它的左右孩子再处理这个结点，如果这个结点是叶子结点就修正codeTable以及codeLengths。

code数组是用来记录自己走过的路，选取左边就尾插0，选取右边就尾插1，top就是code数组的元素个数。注意top是形参，传入的是参数，对于下一个结点，top+1传入过去，对于这个结点的top不会改变。

当遍历到了叶子结点，code数组中存储的就是这个字符对应的二进制数，我们要做的就是把这个二进制数修正到codeTable和codeLengths中。

首先修正codeLengths，top是code数组的元素个数也就是长度，直接赋值就可以了。

接下来修正codeTable，这是一个二维数组，前面的代表每一个字符，后面的代表这个字符对应的二进制数。遍历code数组，依次把二进制修正进去。

---

 编写编码函数

void encodeText(Node* root, char* inputText, char encodedText[], int codeTable[][256], int codeLengths[]) {
	int length = strlen(inputText);
	int i, j;
	for (i = 0; i < length; i++) {
		char character = inputText[i];
		int length = codeLengths[(int)character];
		for (j = 0; j < length; j++) {
			encodedText[strlen(encodedText)] = codeTable[(int)character][j] + '0';
		}
	}
}

 当我们传入一个字符串，把这个字符串编码为对应二进制数存放在encodedText数组中。

用length变量接收传入的字符串的长度，遍历这个字符串中每一个字符，对于每一个字符，用length局部变量接收对应二进制数的长度，接着变量每一个二进制数依次尾插到encodedText数组中，encodedText这个数组是字符数组，而codeTable数组是整型数组，转化过去要用‘0’修正。

---

 编写解码函数

void decodeText(Node* root, char* encodedText, char* decodedText) {
	int length = strlen(encodedText);
	int i = 0;
	
	while (i < length) {
		Node* current = root;
		
		while (current->left != NULL || current->right != NULL) {
			if (encodedText[i] == '0') {
				current = current->left;
			} else if (encodedText[i] == '1') {
				current = current->right;
			}
			i++;
		}
		
		decodedText[strlen(decodedText)] = current->data;
	}
	
	decodedText[strlen(decodedText)] = '\0';
}

 当我们得到一个二进制和他的编码规则（Huffman树）我们就可以对其进行解码。

解码的过程就是依次遍历树，一步一步走，一直到叶子结点为止。

用length变量接收二进制数的长度，用i表示我们访问二进制数的下标。

一开始current指向根结点，只要左右孩子有元素，就一直走下去，如果encodedText是0就走左边，是1就走右边，一直到叶子节点，内循环就停止，此时我们就得到了第一个字符，把这个字符尾插到decodedText数组中。继续从根结点遍历，依次循环。

我可以规定： “A”：000，“B”：001，“C”：010，“D”：011，“E”：100，“F”：101。这样我们就可以把文字内容转化为一段二进制数了，转化后的二进制数是“001000011010000011101100100011”

由00找到第一个字符D修正进decodedText中，接着访问后面的二进制数，由1000找到第二个字符F修正进decodedText中，继续，由01找到第三个字符A修正进decodedText中，继续，由101找到第四个字符C修正进decodedText中........依次循环。

---

 编写主函数

int main() {
	char inputText[] = "Hello,world! I'm glad to meet you!";
	Node* root = buildHuffmanTree(inputText);
	int code[256];
	int top = 0;
	
	
	int codeTable[256][256] = {0};
	int codeLengths[256] = {0};
	
	printf("Huffman Codes:\n");
	printHuffmanCodes(root, code, top, codeTable, codeLengths);
	printf("\n");
	printf("InputText:\n%s\n\n",inputText);
	// 编码文本
	char encodedText[1000] = "";
	encodeText(root, inputText, encodedText, codeTable, codeLengths);
	printf("Encoded Text: \n%s\n\n", encodedText);
	
	// 解码文本
	char decodedText[1000] = "";
	decodeText(root, encodedText, decodedText);
	printf("Decoded Text: \n%s\n\n", decodedText);
	
	return 0;
	
}

 用inputText数组接收需要传入的字符串，用root接收创建的Huffmn树，用codeTable和codeLengths存储编码表，用encodedText存储二进制数，用decodedText存储解码后的字符串。

---

 完整代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct Node {
	char data;
	int frequency;
	struct Node* left;
	struct Node* right;
} Node;

Node* createNode(char data, int frequency) {
	Node* node = (Node*)malloc(sizeof(Node));
	node->data = data;
	node->frequency = frequency;
	node->left = NULL;
	node->right = NULL;
	return node;
}

Node* buildHuffmanTree(char* inputText) {
	int charCount[256] = { 0 };
	int length = strlen(inputText);
	int i;
	
	for (i = 0; i < length; i++) {
		charCount[(int)inputText[i]]++;
	}
	
	Node* nodes[256];
	int nodeCount = 0;
	for (i = 0; i < 256; i++) {
		if (charCount[i] > 0) {
			nodes[nodeCount] = createNode((char)i, charCount[i]);
			nodeCount++;
		}
	}
	
	while (nodeCount > 1) {
		int minFrequency1 = length + 1;
		int minFrequency2 = length + 1;
		int index1 = -1;
		int index2 = -1;
		for (i = 0; i < nodeCount; i++) {
			if (nodes[i]->frequency < minFrequency1) {
				minFrequency2 = minFrequency1;
				index2 = index1;
				minFrequency1 = nodes[i]->frequency;
				index1 = i;
			} else if (nodes[i]->frequency < minFrequency2) {
				minFrequency2 = nodes[i]->frequency;
				index2 = i;
			}
		}
		
		Node* parent = createNode('\0', nodes[index1]->frequency + nodes[index2]->frequency);
		parent->left = nodes[index1];
		parent->right = nodes[index2];
		
		nodes[index2] = parent;
		nodes[index1] = nodes[nodeCount - 1];
		nodeCount--;
	}
	
	return nodes[0];
}

void printHuffmanCodes(Node* root, int code[], int top, int codeTable[][256], int codeLengths[]) {
	if (root->left) {
		code[top] = 0;
		printHuffmanCodes(root->left, code, top + 1, codeTable, codeLengths);
	}
	if (root->right) {
		code[top] = 1;
		printHuffmanCodes(root->right, code, top + 1, codeTable, codeLengths);
	}
	
	if (root->left == NULL && root->right == NULL) {
		codeLengths[(int)root->data] = top;
		printf("%c:",root->data);
		for (int i = 0; i < top; i++) {
			codeTable[(int)root->data][i] = code[i];
			printf("%d",code[i]);
		}
		printf("\n");
	}
}



void encodeText(Node* root, char* inputText, char encodedText[], int codeTable[][256], int codeLengths[]) {
	int length = strlen(inputText);
	int i, j;
	for (i = 0; i < length; i++) {
		char character = inputText[i];
		int length = codeLengths[(int)character];
		for (j = 0; j < length; j++) {
			encodedText[strlen(encodedText)] = codeTable[(int)character][j] + '0';
		}
	}
}

void decodeText(Node* root, char* encodedText, char* decodedText) {
	int length = strlen(encodedText);
	int i = 0;
	
	while (i < length) {
		Node* current = root;
		
		while (current->left != NULL || current->right != NULL) {
			if (encodedText[i] == '0') {
				current = current->left;
			} else if (encodedText[i] == '1') {
				current = current->right;
			}
			i++;
		}
		
		decodedText[strlen(decodedText)] = current->data;
	}
	
	decodedText[strlen(decodedText)] = '\0';
}



int main() {
	char inputText[] = "Hello,world! I'm glad to meet you!";
	Node* root = buildHuffmanTree(inputText);
	int code[256];
	int top = 0;

	
	int codeTable[256][256] = {0};
	int codeLengths[256] = {0};
	
	printf("Huffman Codes:\n");
	printHuffmanCodes(root, code, top, codeTable, codeLengths);
	printf("\n");
	printf("InputText:\n%s\n\n",inputText);
	// 编码文本
	char encodedText[1000] = "";
	encodeText(root, inputText, encodedText, codeTable, codeLengths);
	printf("Encoded Text: \n%s\n\n", encodedText);
	
	// 解码文本
	char decodedText[1000] = "";
	decodeText(root, encodedText, decodedText);
	printf("Decoded Text: \n%s\n\n", decodedText);
	
	return 0;
	
}

---

结尾

在文章的最后，让我们一同总结所探讨的内容。

Huffman树，每个字符出现频率高的离根结点近，出现频率低的离根结点远，每个叶子结点存放字符，走路代表对应二进制数，左边是0，右边是1。

Huffman编码，由Huffman树编码规则得到的二进制数。

Huffman树的构建，统计符号的频率，创建叶子结点数组，依次合并叶子结点。

通过分享这篇文章，我们不仅仅是传递信息，更是建立了一种共鸣和连接。写作是思想的传递，而结尾则是为读者留下深刻印象的重要一环。希望这些文字能够在您的心灵深处激起涟漪，启发更多的思考。

感谢您花时间阅读这篇文章，也欢迎在评论区分享您的想法和反馈。写作是一个不断学习的过程，期待与各位一同成长，共同进步。在未来的创作中，愿我们能够继续交流，共同分享更多有趣的见解。

再次感谢您的关注与支持，期待在下一次的文字交流中与您相遇。祝愿您在写作的旅途中越走越远，创作的天地里开辟出更为辉煌的篇章。

ps.本篇文章有参考《大话数据结构》这本书。