数据结构---用栈实现队列

用栈来模拟一个队列，要求实现队列的两个基本操作：入队、出队。

栈是先入后出，队列是先入先出
用两个栈来实现一个队列功能

让其中一个栈作为队列的入口，负责插入新元素；另一个栈作为队列的出口，负责移除老元素。

核心点：两个栈是各自独立的，怎么能把它们有效地关联起来？

模拟入队

在模拟入队操作时，每一个新元素都被压入到栈A当中。
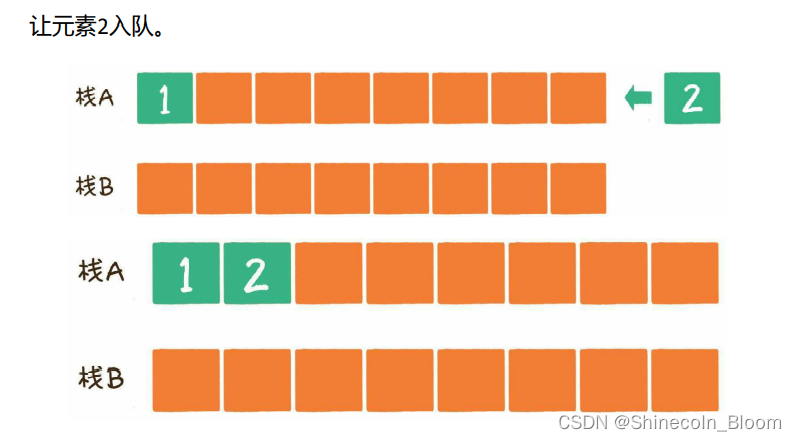
元素1入队

元素2入队

元素3入队

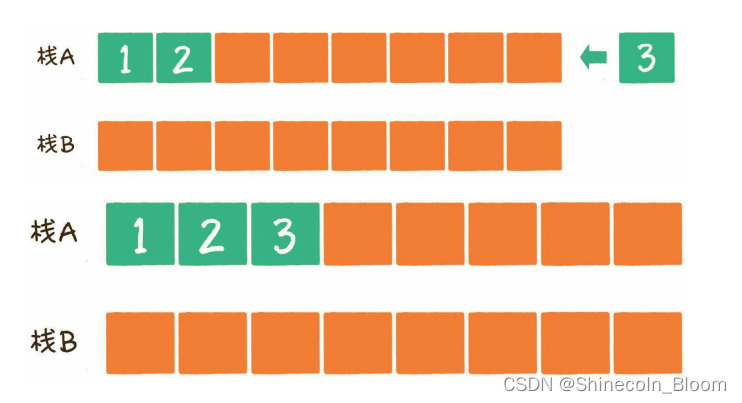
模拟出队

按理说，我们希望最先入队的元素1出队

解决方案：让栈A中的所有元素按顺序出栈，再按照出栈顺序压入栈B。这样一来，元素从栈A弹出并压入栈B的顺序是3、2、1，和当初进入栈A的顺序1、2、3是相反的。

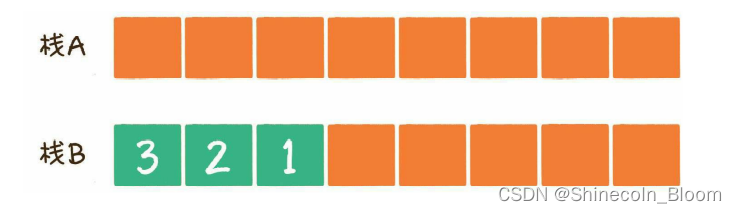
此时让元素1 出队，也就是让元素1从栈B中弹出。

让元素2出队。

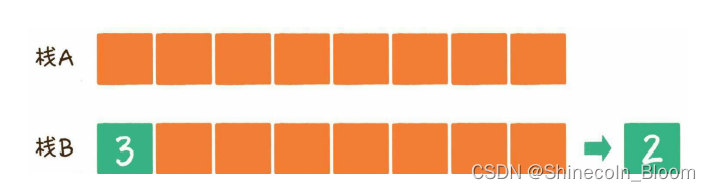
如果现在又有新元素4入队：

每次都是先把栈B弹干净后，再从栈A取元素入栈到B中

先把3弹栈，这时，栈B为空栈，再从栈A中取元素到B中。

JAVA实现

package algorithmProblem;
import java.util.Stack;

//栈模拟队列的入队和出队
public class stacks2Queue {
    //用俩个栈模拟
    private Stack<Integer> stackA = new Stack<Integer>();
    private Stack<Integer> stackB = new Stack<Integer>();

    /**
     * 入队
     * @param element
     */
    public void enQueue(int element){
        stackA.push(element);
    }

    /**
     * 栈A元素转移到栈B
     * 为了出队做的前期准备
     */
    private void transformer(){
        //当栈A不为空，执行循环(把A栈元素全部都放到B栈中)
        while (!(stackA.isEmpty())) {
            stackB.push(stackA.pop());
        }
    }

    /**
     * 出队操作
     * @return
     */
    public Integer deQueue(){
        if(stackB.isEmpty()){
            //队列为空的返回条件
            if(stackA.isEmpty()){
                System.out.println("队列没有元素了");
                return null;
            }
            //队列不为空，并且再stackB为空的情况下，把stackA转移到B，用于出栈
            transformer();
        }

        //栈B不为空，就对B栈出栈，直到为空，才往B栈放元素
        return stackB.pop();
    }

}

测试类：

package algorithmProblem;

public class stacks2QueueTest {
    public static void main(String[] args) {
        stacks2Queue myqueue = new stacks2Queue();
        myqueue.enQueue(1);
        myqueue.enQueue(2);
        myqueue.enQueue(3);
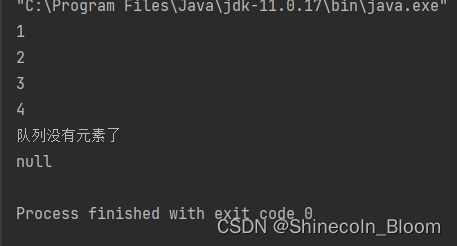
        System.out.println(myqueue.deQueue());
        System.out.println(myqueue.deQueue());
        myqueue.enQueue(4);
        System.out.println(myqueue.deQueue());
        System.out.println(myqueue.deQueue());
        System.out.println(myqueue.deQueue());

    }
}

总结

入队操作的时间复杂度显然是O(1)
出队的时间复杂度：
如果涉及栈A和栈B的元素迁移，那么一次出队的时间复杂度是O(n)；
如果不用迁移，时间复杂度是O(1)。

均摊时间复杂度:需要元素迁移的出队操作只有少数情况，并且不可能连续出现，其后的大多数出队操作都不需要元素迁移。所以把时间均摊到每一次出队操作上面，其时间复杂度是O(1)。