动态规划（dp）初步学习案例讲解

问题（来源：leetcode300）：

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

举例说明：

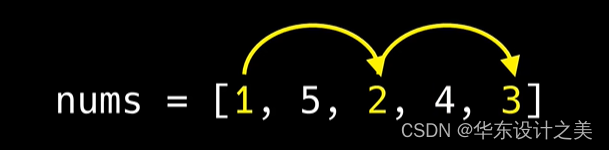
从上述案例nums可以看出（1 2 4）或者（1 2 3）都可以是最长的一个答案，而我们只要求出他的长度即可。

方案一，暴力穷举：

暴力穷举往往是最简单也最容易想到的，通过一步步逐步筛选，逐步搜索进行穷举。将其通过循环逐步套取，把每个子序列都进行一遍搜索，完成答案的求解，取最长数列长度即可。

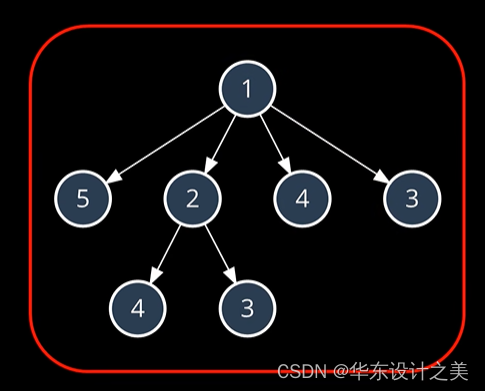
通过一个getLen函数进行最长子序列的求取，需要注意的是，当i取到序列的最后一位时，返回长度1，停止搜索，而当你本身被搜索时就是一个长度单位，所以每次搜索的maxlen初始长度为1。

时间复杂度：假定数组长度为n，即可生成2^n个子序列（数组中的每个数字可以选择取用或者不取用两个方式，n个长度，即可为2^n个），每个子序列都需要进行n次遍历，即为O（n），所以时间复杂度为O(2^n)*O(n)。

#include <iostream>
#include <algorithm> 
#include <cmath> 
#include <vector> 
#include <chrono>

using namespace std;

int getLen(vector<int> num, int i) {
    if (i == num.size() - 1) return 1;
    int maxlen = 1;
    for (int j = i + 1;j < num.size();j++) {
        if (num[j] > num[i]) {
            maxlen = max(maxlen, getLen(num, j) + 1);
        }
    }
    return maxlen;
}

int main() {
    auto start = chrono::high_resolution_clock::now(); // 记录开始时间
    int nums[25] = { 1,5,2,4,3,7,15,35,61,2,58,64,9,15,3,44,12,33,65,15,22,49,85,2,34};
    int ans = 0;
    vector<int> num(nums, nums +25);
    for (int i = 0;i < num.size();i++) {
        ans = max(ans, getLen(num, i));
    }
    cout << ans << endl;
    auto end = chrono::high_resolution_clock::now(); // 记录结束时间
    auto duration = chrono::duration_cast<chrono::microseconds>(end - start); // 计算程序运行时间
    cout << "程序运行时间：" << duration.count() << "微秒" << endl;
    return 0;
}

算法优化：空间换时间

方案二，用哈希进行回溯剪枝：

由于在暴力穷举的过程中，存在当你访问过一个数据时又一次访问该数据，即如图，第一次在（1 2 4）中已经检索过4，而在后续过程中又一次访问了4（1 4），即可用空间来换取时间，创建一个哈希表进行记录存储最大子序列长度，即可减少访问步骤。

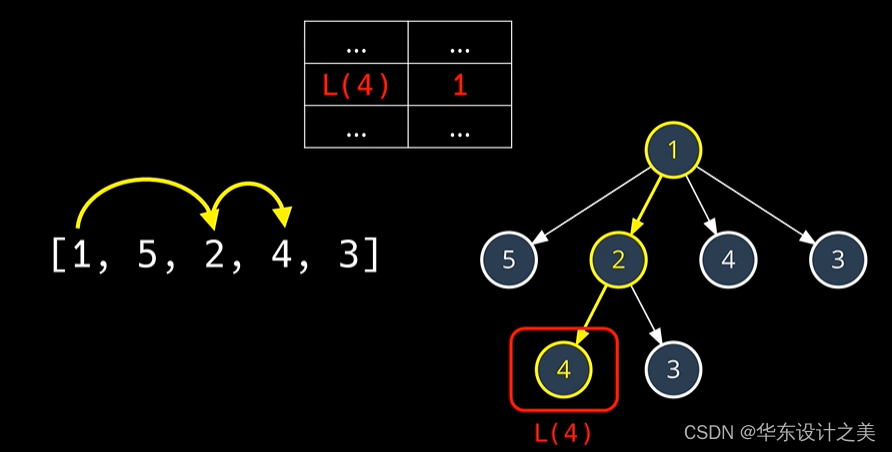
依然是通过getLen方法来获取最大子序列长度，不过本次加入了memo哈希表来进行数据存储，当memo中数据非0时，即表明该处内容已被检索，即可直接返回memo[i]，减少搜索时间。

时间复杂度大大减少

#include <iostream>
#include <algorithm> 
#include <cmath> 
#include <vector> 
#include <chrono>

using namespace std;
vector<int> memo(25);

int getLen(vector<int> num, int i) {
    if (i == num.size() - 1) return 1;
    if (memo[i] != 0) return memo[i];
    int maxlen = 1;
    for (int j = i + 1;j < num.size();j++) {
        if (num[j] > num[i]) {
            maxlen = max(maxlen, getLen(num, j) + 1);
        }
    }
    memo[i] = maxlen;
    return maxlen;
}

int main() {
    auto start = chrono::high_resolution_clock::now(); // 记录开始时间
    int nums[25] = { 1,5,2,4,3,7,15,35,61,2,58,64,9,15,3,44,12,33,65,15,22,49,85,2,34 };
    int ans = 0;
    vector<int> num(nums, nums + 25);
    for (int i = 0;i < num.size();i++) {
        ans = max(ans, getLen(num, i));
    }
    cout << ans << endl;
    auto end = chrono::high_resolution_clock::now(); // 记录结束时间
    auto duration = chrono::duration_cast<chrono::microseconds>(end - start); // 计算程序运行时间
    cout << "程序运行时间：" << duration.count() << "微秒" << endl;
    return 0;
}

方案三，改写成迭代形式：

通过反推的方式，从序列最后一位开始寻找最长子序列，逐步倒推归纳迭代，一直访问到第一位时的最长子序列，即可完成数据的搜寻访问。

实现方式：通过getLen方法来获取子序列最长长度，通过倒序搜索来寻找子序列中各自的最长数组长度，i从倒数第二位开始访问，由于倒数第一位一定是1，一直搜索到第一位，而j则是通过i+1到最后一位进行搜索，在找完各自的最长数组后，进行排序，找出最大值即可。

时间复杂度：由于只进行了两个循环，即为O(n^2)。

#include <iostream>
#include <algorithm> 
#include <cmath> 
#include <vector> 
#include <chrono>

using namespace std;

int getLen(vector<int> num) {
    int n = num.size();
    vector<int> L(n,1);
    for (int i = n-2;i>=0;i--) {
        for (int j = i + 1;j < n;j++) {
            if (num[j] > num[i]) L[i] = max(L[i], L[j] + 1);
        }
    }
    sort(L.begin(), L.end());
    return L[n-1];
}

int main() {
    auto start = chrono::high_resolution_clock::now(); // 记录开始时间
    int nums[25] = { 1,5,2,4,3,7,15,35,61,2,58,64,9,15,3,44,12,33,65,15,22,49,85,2,34 };
    int ans = 0;
    vector<int> num(nums, nums + 25);
    cout << getLen(num) << endl;
    auto end = chrono::high_resolution_clock::now(); // 记录结束时间
    auto duration = chrono::duration_cast<chrono::microseconds>(end - start); // 计算程序运行时间
    cout << "运行时间：" << duration.count() << "微秒" << endl;
    return 0;
}

动态规划思路总结：

使用穷举法完成暴力搜索，可画出递归树
在搜索过程中发现重复搜索的痕迹，即可用哈希表进行数据回溯剪枝
将计算的过程用迭代的方式表示出来