两数求最大公因数的方法(基于c语言编程）

一、枚举寻找法

1.简要阐述

        这个方法相对容易理解，并且方便记忆，但效率较低，因为毕竟这是暴力枚举。逻辑其实就是两个数字找出其中的较小数，从这个数依次减一，在两个数字同时整除一个数的时候，将其输出，这便是二者的最大公约数。

2.相关代码

         为方便得到结果，不妨直接取84和32。

#include <stdio.h>
int main(void)
{
    int a=84,b=32;
    int i;
    for(i=32;i>=1;i--)
    {
        if(a%i==0&&b%i==0)
        {
            printf("%d",i);
            break;
        }
    }
    return 0;
}

 二、辗转相除法

1.推导过程

        需求a，b两数的最大公因数，假设a大于b，因此便设a=b*m+r (r<b)，m为a除以b所得商，r为对应余数，我们希望存在一个等式，使等式两边的数字呈整数倍的关系，因此希望找到一种迭代的方式来求解，这其实就是辗转相除法的主要核心方法，所以证明过程也要向这个方向上靠近。

        不妨令a与b的最大公因数为c，然后用p，q两整数表示出a和b，即a=p*c，b=q*c，然后将这两个关系式代入a=b*m+r，得p*c=q*m*c+r，移项得r=(p-qm)*c，观察比较二式b=q*c和r=(p-qm)*c可知，b和r的最大公约数C是大于等于c的，由式子a=b*m+r可知，a也有一个因数是C，已知a与b的最大公因数为c，因此c大于等于C，与“b和r的最大公约数C是大于等于c的”条件结合可得，c等于C，所以证明出了a，b与b，r的最大公因数是一样的。

        接下来其实就是辗转相除法的运用的理解，就是用除数代替被除数，余数代替除数，以此为迭代公式进行运算，直至运算后余数为0，此时的除数就是要求的最大公因数。

        我们可以用一个流程图更为直观的看出迭代过程。

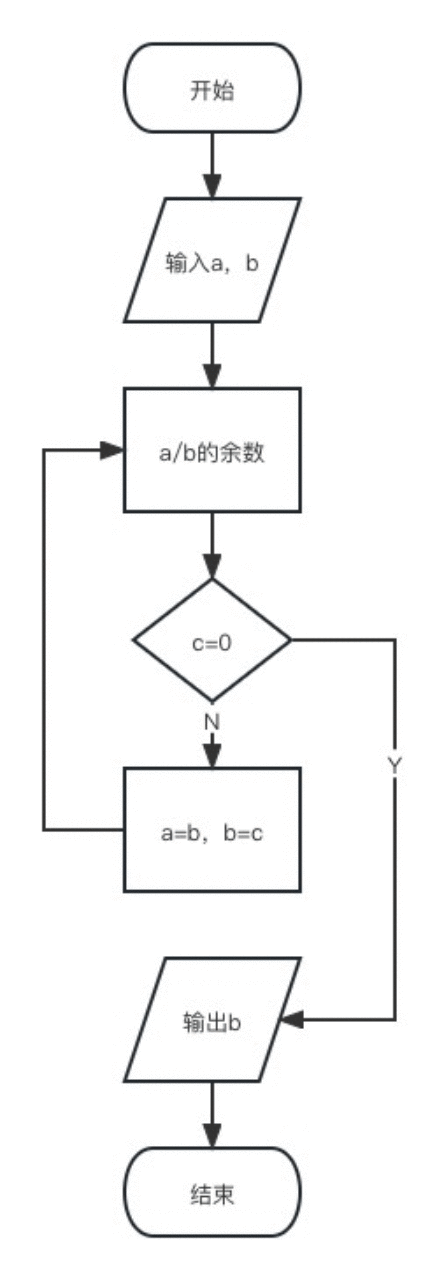
        原来找到了一个不太正确的图更能说明辗转相除法的优势，就是不用像第一个方法去找哪个数小，在迭代过程中这一步可以自然地去实现。 

2.相关代码

#include <stdio.h>
int main(void)
{
    int a,b,r;
    scanf("%d%d",&a,&b);
    r=a%b;
    while(r!=0)
    {
        r = a%b;
        a = b;
        b = r;
    }
    printf("%d\n",a);
    return 0;
}

        因为一开始写这个代码就是根据之前推导过程写的，因此一开始我直接输出的是b，所以想再简单说明一下，while循环结束的标志是r变为0，但结束的前一个循环运算已经是a，b可以整除了，即r=0，该次循环中将b，即最大公约数的值赋给了a，r的0值赋给了下一个状态下的b，但我们其实要的应该是a，将其输出就可以了。