RIS-Assisted Communication Radar Coexistence:Joint Beamforming Design and Analysis
1、基本内容:
未来无线通信系统需要更高的数据传输率和和智能感知服务,这就对频谱资源提出了更高的需求。一方面,我们可以将频谱向高频拓展。另一方面,在多个系统之间实现频谱共享。由于雷达和通信系统在硬件、信号处理等许多方面的相似性,ISAC被提出来。ISAC有两个层面,低层面来说,就是只共享频谱,对应的系统是通信雷达共存系统,研究难点是互干扰管理;更高层面就是不仅共享频谱,还共享设备,也就是双功能雷达通信系统(DFRC),研究难点是ISAC波形的设计。
本文考虑的是通信雷达共存系统,为了消除互干扰,作者将两个RIS引入系统,一个部署在发射器抑制发射器对雷达的干扰,一个部署在接收器抑制雷达对接收器的干扰。
作者考虑了雷达功率较大和较小两种场景。
本文的目标是通过联合优化雷达的有源波束形成矩阵和RIS的无源波束形成矩阵来最大化通信性能,同时确保雷达发射功率约束下的雷达检测性能。作者考虑用双环罚对偶分解double-loop penalty dualdecomposition (PDD)求解。
2、系统模型:
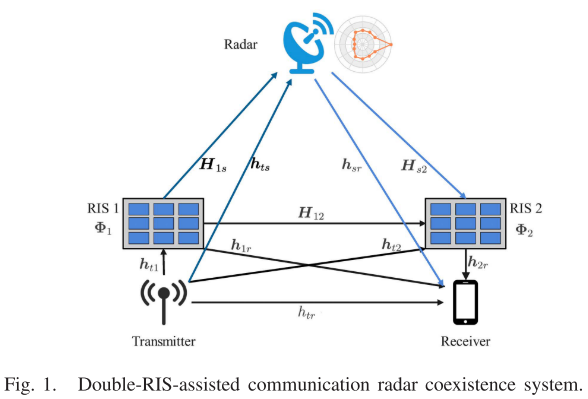
雷达探测方向: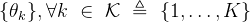
脉冲重复间隔(PRI):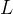
雷达发射的脉冲信号:
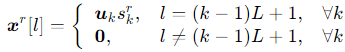
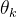 方向的发射功率:
方向的发射功率: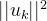
发射信号经过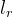 的时间才被接收。
的时间才被接收。
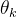 方向的回波:
方向的回波:![\boldsymbol{y}_k^{r,e}[l]=\alpha_k\boldsymbol{a}(\theta_k)\boldsymbol{a}^T(\theta_k)\boldsymbol{x}^r[l-l_r]](https://images2.imgbox.com/83/d7/0vfmvdB0_o.png)
通信对感知的干扰:“发射机-雷达”和“发射机-RIS1-雷达”。
![\boldsymbol{y}_{k}^{r,i}[l]=(\boldsymbol{h}_{ts}+\boldsymbol{H}_{ts}\boldsymbol{\phi}_{1})\sqrt{p^{c}}s^{c}[l]](https://images2.imgbox.com/76/34/qSQ6YhvW_o.png)
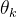 方向的感知SINR:
方向的感知SINR:
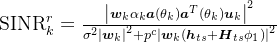
————————————————————————————————————————
用户接收的想要的通信信号:![\begin{aligned}y^{c}[l]=\left(h_{tr}+g_{tr}^H\phi_1+f_{tr}^H\phi_2+\phi_1^TH_{tr}\phi_2\right)\sqrt{p^c}s^c[l]\end{aligned}](https://images2.imgbox.com/0d/22/0UNtSsSF_o.png)
感知对通信的干扰:“雷达-接收器”和“雷达-RIS2-接收器”
![\begin{aligned}y^i[l]=\begin{pmatrix}h_{sr}^H+\phi_2^TH_{sr}\end{pmatrix}x^r[l]\end{aligned}](https://images2.imgbox.com/e6/b7/YOMLq31t_o.png)
整个epoch的平均通信SINR:
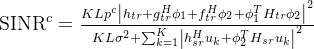
3、优化问题:
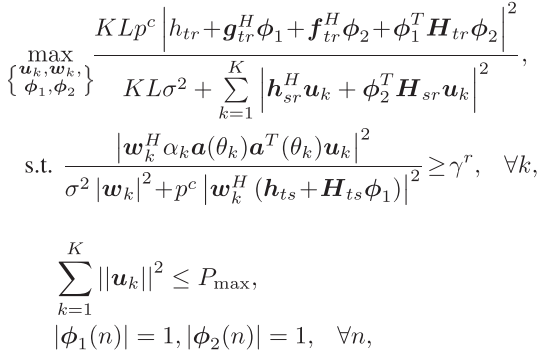
——————————————————内环————————————————————
作者考虑在PDD框架下求解,难点在于目标函数是分式项以及感知约束中变量高度耦合。
对于目标函数,利用分式规划(FP)求解。
对于感知约束,引入辅助变量,来替换耦合部分。
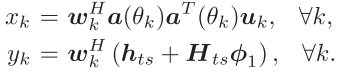
感知约束变为: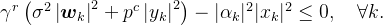
将辅助变量引入的等式约束通过罚因子加入到广义拉格朗日函数中。
感知约束变成了一个difference-of-convex (DC)函数,可以使用concave-convex procedure (CCCP)进行处理。然后利用块坐标下降(BCD)求解。
——————————————————外环—————————————————————
更新罚因子和对偶变量。
罚因子以常数衰减。
对偶变量通过KKT条件更新。
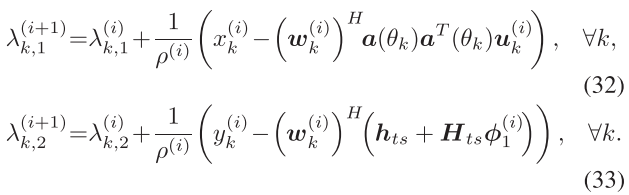
外环终止条件:约束违反在容忍范围外就终止。
约束违反程度:
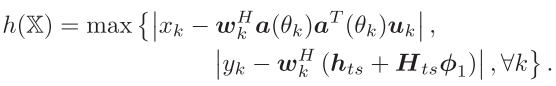
—————————————————更新流程————————————————————
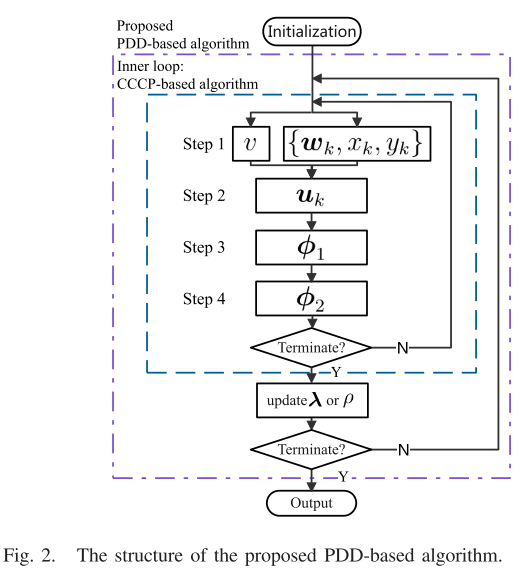
参考文献