不规则图形数格子的方法_小学数学，怎么数平面图形中长方形与正方形个数

昨天我们说了线段的两种计数方法，一种是数端点的方法，也叫打枪法，或者叫大炮发射法，另一种是分类法。而且我们着重推荐使用分类法。今天我们继续说说平面图形的计数问题。

今天这里着重说一下，长方形以及正方形的计数。

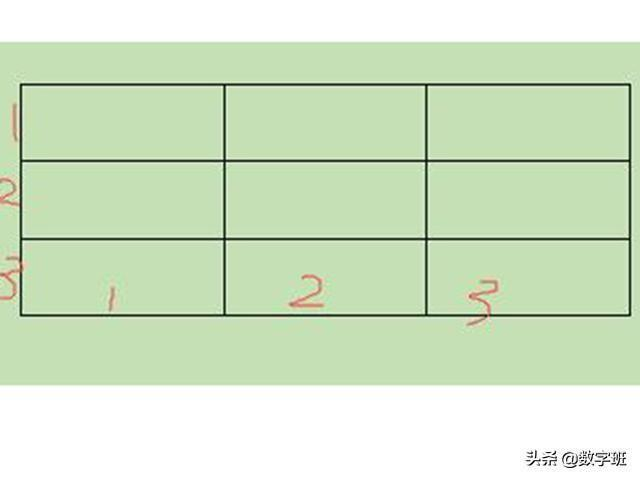
当一个图形是长方形，只是一层的话，相信这个都很简单，大家都知道他跟数线段其实是一样的道理，那么有几个基本的长方形，根据公式，就可以很快的算出来。

如果说是有多层的话，我们是怎么算呢？其实也是可以根据分类的原理，套用公式。比如说上图中横向有3个基本长方形，纵向也有3个基本长方形，我们如何算呢？

那我们算一下横向有3+2+1=6个，纵向其实是一样的3+2+1=6个，那么这个三行三列的图形中，总共就有：6×6=36个长方形。

我们再说一下全部由小正方形组成的平面图形，怎么数正方形个数？比如一个4行4列，每一小格都是正方形组成的平面图形，总共有多少个正方形？这种图形不按顺序不分类很容易数错。

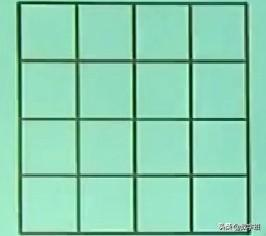
由于这些格子全部是正方形，所以从1行1列，到4行4列全都是正方形。我们也是把它分按照分类。单独一格一格的；田字格的，就是2行2列的；3行3列的，以及4行4列的这四种正方形。

单独一格小正方形这种很简单，我们可以数一下横向有4个，纵向有4个。4×4=16个。

那么这种田字格的那有多少呢？我们可以数一下3×3=9个。九宫格的有多少个呢？有2×2=4个，4行4列的就只有最外面1个。

然后我们将这些全部加起来，算出来的总数就是整个图形中正方形的个数。

16+9+4+1=30个。

如果在旁边再加一列这样的小正方形，变成了4行5列的图形，总共会有多少个正方形呢？

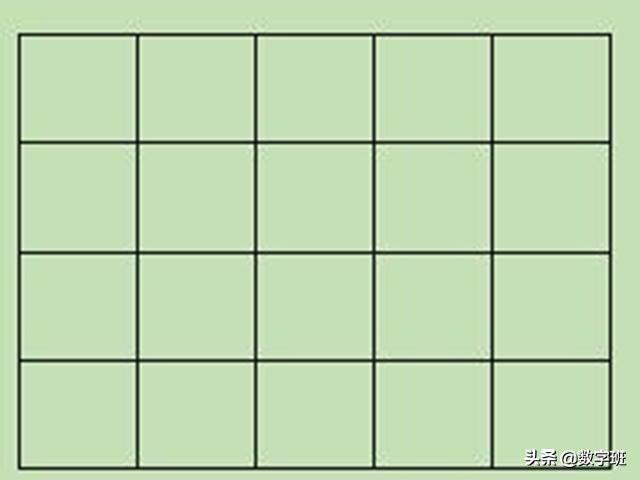
4行5列

单格的：4×5=20(个)

田字格：3×4=12(个)

九宫格：2×3=6(个)

四行四列的：1×2=2(个)

这图形中有没有更大的正方形了？当然没有，图形本身才是4行5列，所以最大的就是4行4列的那2个正方形。

将这四种规格的正方形数量全部相加：20+12+6+2=40(个)

平面图形计数一定记得以某种顺序，比如上图中寻找隐藏在树中的10个人头，我们就是用从上到下，从左到右的顺序来找的。如果看到一个标一个，杂乱无章的，出错的机会远远大于数对的概率。

都说条条大道通罗马，每个人的方法可能不一样，欢迎大家在评论中留下你的好方法。