由空间三对点求解两个坐标系之间的变换矩阵
三维刚体变换模型(即旋转/平移矩阵,RT矩阵)的估计方法
原理简单阐述:
只要算出变换矩阵,就可以算出A坐标系的一个点P在坐标系B里的对应点坐标,即
![]()
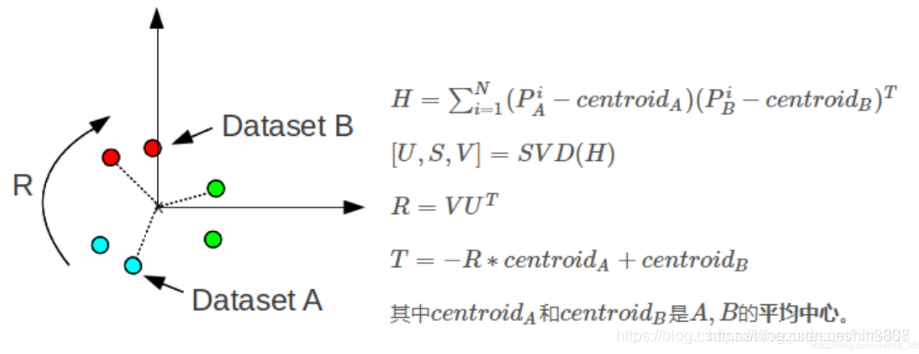
T为3x3的转换矩阵, t 为3x1的位移变换向量,这里点坐标均为3x1的列向量(非齐次形式,齐次形式下为4x1列向量,多出的一个元素值补1而已)。理论上只要给定至少3对点,就能计算出 T 和 t 。自然的,点对越多,计算出来的转换就越精确。详细的原理请参考《Estimating 3-D Rigid Body Transformations: A Comparison of Four Major Algorithms》,它使用SVD方法计算 T 和 t 。
下面就话不多说,上代码。亲写亲测有效
cv::Mat Get3DR_TransMatrix(const std::vector<cv::Point3f>& srcPoints, const std::vector<cv::Point3f>& dstPoints)
{
double srcSumX = 0.0f;
double srcSumY = 0.0f;
double srcSumZ = 0.0f;
double dstSumX = 0.0f;
double dstSumY = 0.0f;
double dstSumZ = 0.0f;
//至少三组点
if (srcPoints.size() != dstPoints.size() || srcPoints.size() < 3)
{
return cv::Mat();
}
int pointsNum = srcPoints.size();
for (int i = 0; i < pointsNum; ++i)
{
srcSumX += srcPoints[i].x;
srcSumY += srcPoints[i].y;
srcSumZ += srcPoints[i].z;
dstSumX += dstPoints[i].x;
dstSumY += dstPoints[i].y;
dstSumZ += dstPoints[i].z;
}
cv::Point3d centerSrc, centerDst;
centerSrc.x = double(srcSumX / pointsNum);
centerSrc.y = double(srcSumY / pointsNum);
centerSrc.z = double(srcSumZ / pointsNum);
centerDst.x = double(dstSumX / pointsNum);
centerDst.y = double(dstSumY / pointsNum);
centerDst.z = double(dstSumZ / pointsNum);
//Mat::Mat(int rows, int cols, int type)
cv::Mat srcMat(3, pointsNum, CV_64FC1);
cv::Mat dstMat(3, pointsNum, CV_64FC1);
---Modify
for (int i = 0; i < pointsNum; ++i)//N组点
{
//三行
srcMat.at<double>(0, i) = srcPoints[i].x - centerSrc.x;
srcMat.at<double>(1, i) = srcPoints[i].y - centerSrc.y;
srcMat.at<double>(2, i) = srcPoints[i].z - centerSrc.z;
dstMat.at<double>(0, i) = dstPoints[i].x - centerDst.x;
dstMat.at<double>(1, i) = dstPoints[i].y - centerDst.y;
dstMat.at<double>(2, i) = dstPoints[i].z - centerDst.z;
}
cv::Mat matS = srcMat * dstMat.t();
cv::Mat matU, matW, matV;
cv::SVDecomp(matS, matW, matU, matV);
cv::Mat matTemp = matU * matV;
double det = cv::determinant(matTemp);//行列式的值
double datM[] = { 1, 0, 0, 0, 1, 0, 0, 0, det };
cv::Mat matM(3, 3, CV_64FC1, datM);
cv::Mat matR = matV.t() * matM * matU.t();
double* datR = (double*)(matR.data);
double delta_X = centerDst.x - (centerSrc.x * datR[0] + centerSrc.y * datR[1] + centerSrc.z * datR[2]);
double delta_Y = centerDst.y - (centerSrc.x * datR[3] + centerSrc.y * datR[4] + centerSrc.z * datR[5]);
double delta_Z = centerDst.z - (centerSrc.x * datR[6] + centerSrc.y * datR[7] + centerSrc.z * datR[8]);
//生成RT齐次矩阵(4*4)
cv::Mat R_T = (cv::Mat_<double>(4, 4) <<
matR.at<double>(0, 0), matR.at<double>(0, 1), matR.at<double>(0, 2), delta_X,
matR.at<double>(1, 0), matR.at<double>(1, 1), matR.at<double>(1, 2), delta_Y,
matR.at<double>(2, 0), matR.at<double>(2, 1), matR.at<double>(2, 2), delta_Z,
0, 0, 0, 1
);
return R_T;
}
以下是简单自测代码:
int main()
{
std::vector<cv::Point3f> srcPoints;
std::vector<cv::Point3f> dstPoints;
//模拟绕Z轴转90度,再X轴平移50.
//取三组点
float NN = 100;
srcPoints.push_back(cv::Point3f(NN, 0, 0));
dstPoints.push_back(cv::Point3f(50+0, NN, 0));
srcPoints.push_back(cv::Point3f(0, NN, 0));
dstPoints.push_back(cv::Point3f(50 -NN, 0, 0));
srcPoints.push_back(cv::Point3f(0, 0, NN));
dstPoints.push_back(cv::Point3f(50+0, 0, NN));
cv::Mat RT = Get3DR_TransMatrix(srcPoints, dstPoints);
for (int r = 0; r < RT.rows; r++)
{
for (int c = 0; c < RT.cols; c++)
{
printf("%f, ", RT.at<double>(r, c));
}
printf("\n");
}
printf("**************************************\n");
getchar();
}
执行结果:
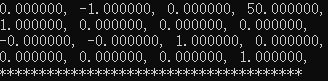
说明:
这个方法对固定的两个坐标系 转换矩阵比较精确,对于实际测量的数据,比如:GPS测量的位置数据,VIO测量的位置数据,因为他们之间存在噪声,此时得到的转换矩阵是不准确的,大多情况下都是不准确的!这个时候应该考虑基于优化的方法!