信号与系统复习笔记——采样

信号与系统复习笔记——采样与通讯系统

采样定理

冲激串采样函数可表示为：

$$p(t)=\sum _{n=-\infty }^{+\infty }\delta (t-nT)$$

周期 $T$ 称为采样周期，而 ${\omega }_s=\frac{1}{T}$ 为采样频率。

对信号 $x(t)$ 进行冲激串采样的结果为：

$$x_p(t)=x(t)p(t)=\sum _{n=-\infty }^{+\infty }x(nT)\delta (t-nT)$$

$x_p(t)$ 本身仍是一个冲激串，幅度为 $x(t)$ 在采样点上的值。

并且有：

$$X_p(j\omega )=\frac{1}{2\pi }[X(j\omega )\ast P(j\omega )]$$

其中：

$$P(j\omega )=\frac{2\pi }{T}\sum _{k=-\infty }^{+\infty }\delta (\omega -k{\omega }_s)$$

已知信号和单位冲激函数做卷积等于该信号的位移：

$$X(j\omega )\ast \delta (\omega -{\omega }_0)=X(j(\omega -{\omega }_0))$$

于是有：

$$X_p(j\omega )=\frac{1}{T}\sum _{k=-\infty }^{+\infty }X(j(\omega -k{\omega }_s))$$

即 $X_p(j\omega )$ 频谱是 $X(j\omega )$ 频谱以周期 $T$ 出现并叠加得到的结果，若频谱无重叠，那么则可以通过低通滤波器得到原信号频谱，这称为 采样定理 ：

设 $x(t)$ 是一个带限信号，在 $|\omega |>{\omega }_M$ 的时候 $X(j\omega )=0$ 。如果 ${\omega }_s>2{\omega }_M$ ，那么 $x(t)$ 就可以被频率为 ${\omega }_s$ 的周期采样串所采样并且唯一的确定。

其中2倍最大频率 $2{\omega }_M$ 称为 奈奎斯特频率 。

零阶保持采样

实际上传输窄和幅度较大的脉冲是相当困难的，我们可以采用零阶保持的方法来进行采样，即在采样的瞬间，直到下一次采样点来临，都是一直保持这一样本值：

这相当于，冲激采样之后，在串联一个零阶保持器：

零阶保持器具有一个从0开始的矩形窗口的单位脉冲响应，并且保持时间为采样频率 $T$ 。

利用插值重建信号

插值，就是用一连续信号对一组样本值的拟合。常见的插值方法有：零阶保持插值、线性插值，多项式插值等。

对于冲激串采样的结果 $x_p(t)$ 来说，通入截止频率为 ${\omega }_M$ 的低通滤波器即可还原成源信号，这在时域上相当于做卷积：

$$x_r(t)=x_p(t)\ast h(t)={\int }_{-\infty }^{+\infty }h(t-\tau )\sum _{n=-\infty }^{+\infty }x(nT)\delta (\tau -nT)d\tau =\sum _{n=-\infty }^{+\infty }x(nT){\int }_{-\infty }^{+\infty }h(t-\tau )\delta (\tau -nT)d\tau =\sum _{n=-\infty }^{+\infty }x(nT)h(t-nT)$$

上式体现了低通滤波器的冲激响应曲线的拟合插值过程：

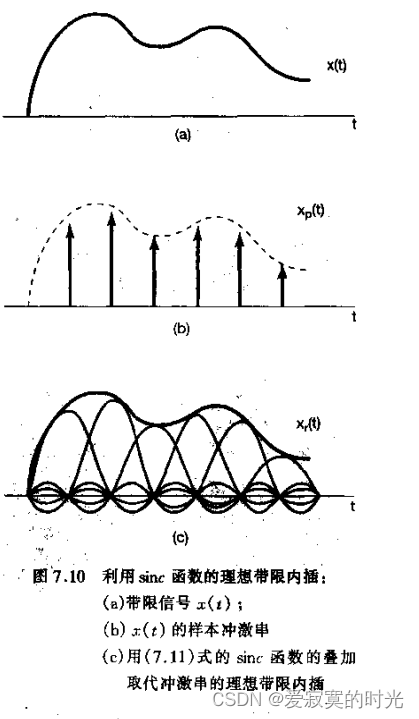
对一个理想的低通滤波器来说，其：

$$h(t)=T\frac{\sin ({\omega }_{c}t)}{\pi t}$$

这种插值方式通常称为 带限插值 。

理想滤波器物理上是不存在的，因此我们通常使用近似的非理想滤波器，会对信号还原造成一定损失，例如零阶保持器，在零阶保持采样中，可以将零阶保持器视为一个低通滤波器，其频率响应和理想滤波器相比如下：

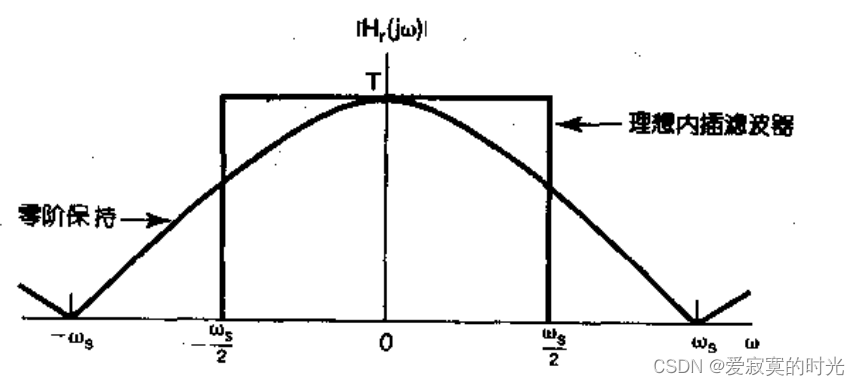
若零阶保持器效果不好，可采用高阶保持器，这里的阶数指，插值后的函数曲线最高在该阶数的导数连续，例如零阶保持器表示在零阶导数都不连续，而线性插值（一阶保持器）表示在零阶导数连续，一阶导数不连续。

易知线性插值的冲激响应是如图的三角波形：

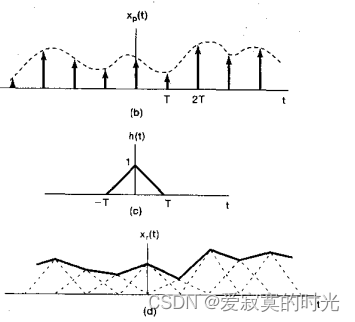
其频率响应和理想滤波器相比如下：

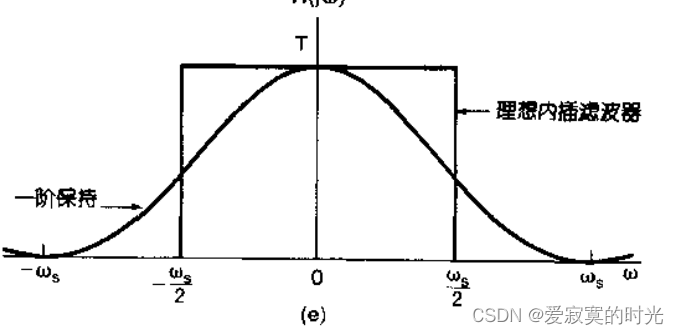
其频率响应为：

$$H(j\omega )=\frac{1}{T}[\frac{\sin (\omega T/2)}{\omega /2}{]}^2$$

欠采样

当 ${\omega }_s>2{\omega }_M$ 的时候，采样信号的频谱是由原信号频谱重复组成，当 ${\omega }_s>2{\omega }_M$ 的时候，采样信号的频谱不再是重复原信号频谱，而是发生 混叠现象 ，因此利用低通滤波器也不能把信号还原出来。

显然，对于采样点上的信号值通常能够准确的还原出来，即：

$$x_r(nT)=x(nT)$$

我们使用 $x(t)=\cos {\omega }_{0}t$ 来说明欠采样的效果，当采用不同的采样频率的时候：

$$\begin{array}{cc}{x}_r(t)=\cos {\omega }_{0}t=x(t)& {\omega }_0=\frac{{\omega }_s}{6}\\ x_r(t)=\cos {\omega }_{0}t=x(t)& {\omega }_0=\frac{2{\omega }_s}{6}\\ x_r(t)=\cos [({\omega }_s-{\omega }_0)t]\ne x(t)& {\omega }_0=\frac{4{\omega }_s}{6}\\ x_r(t)=\cos [({\omega }_s-{\omega }_0)t]\ne x(t)& {\omega }_0=\frac{5{\omega }_s}{6}\end{array}$$

当混叠发生的时候，原始频率 ${\omega }_0$ 就被混叠成一个较低的频率 ${\omega }_s-{\omega }_0$ 。当 ${\omega }_0={\omega }_s$ 的时候，被重建的信号就是一个常数。

对于带相位的 $x(t)=\cos ({\omega }_{0}t+\varphi )$ 来说，傅里叶变换的形状是相同的，只不过在 ${\omega }_0$ 的位置的冲激有个幅度因子 $\pi e^{j\varphi }$ 在 $-{\omega }_0$ 的时候冲激有个幅度因子 $\pi e^{-j\varphi }$ ，当发生混叠的时候，此时：

$$x_r(t)=\cos [({\omega }_s-{\omega }_0)t-\varphi ]$$

这个在相位上有个颠倒，称为 相位倒置 。

最后需要注意一点是，采样定理一定是采样频率大于信号最大频率的2倍，等于是不够的，考虑：

$$x(t)=\cos (\frac{{\omega }_s}{2}t+\varphi )$$

若通过频率 ${\omega }_s$ 采样，得到的输出为：

$$x_r(t)=\cos \varphi \cos (\frac{{\omega }_s}{2}t)$$

可见只有当 $2\pi$ 倍相位偏移的时候，才能正确还原。

连续时间信号的离散时间处理

连续时间信号的离散时间处理的基本框架为：

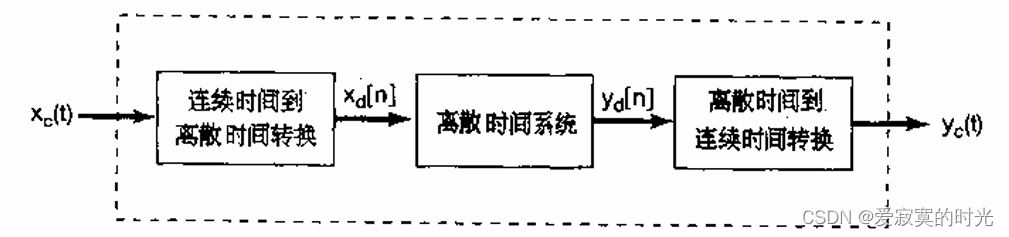
其中 $x_c(t)$ 表示原始连续时间信号， $x_d[n]$ 表示采样的离散信号， $y_d[n]$ 表示经过离散时间系统处理后的离散信号， $y_c(t)$ 表示处理后的连续时间信号。

根据采样定理（采样频率满足采样定理），连续时间信号就可以完全使用其采样样本值代替：

$$x_d[n]=x_c(nT)$$

这一步称为 连续时间到离散时间转换 ，简称C/D。第三步是 离散时间到连续时间转换 ，简称D/C，其实现的是样本值之间的插值。因为大部分的信号处理系统都是数字系统，这样用于实现C/D的器件就称为 模拟数字A/D转换器 ，而实现D/C的器件就称为 数字模拟D/A转换器 。

实现C/D可以对 $x_c(t)$ 进行冲激串采样，再将得到的采样冲激串序列转换为离散点值序列。

通过傅里叶变换来分析这个过程，我们记 $x_c(t)$ 变换为 $X_c(j\omega )$ ，记 $y_c(t)$ 变换为 $Y_c(j\omega )$ 而记 $x_d[n]$ 变换为 $X_d(e^{j\Omega })$ ，记 $y_d[n]$ 变换为 $Y_d(e^{j\Omega })$ 。

已知：

$$x_p(t)=\sum _{n=-\infty }^{+\infty }{x}_c(nT)\delta (t-nT)$$

而 $\delta (t-nT)$ 的傅里叶变换为 $e^{-j\omega nT}$ ：

$$X_p(j\omega )=\sum _{n=-\infty }^{+\infty }{x}_c(nT)e^{-j\omega nT}$$

现在考虑 $x_d[n]$ 的傅里叶变换：

$$X_d(e^{j\Omega })=\sum _{n=-\infty }^{+\infty }{x}_d[n]e^{-j\Omega n}$$

带入 $x_d[n]=x_c(nT)$ 得到：

$$X_d(e^{j\Omega })=\sum _{n=-\infty }^{+\infty }{x}_c(nT)e^{-j\Omega n}$$

我们发现：

$$X_d(e^{j\Omega })=X_p(j\Omega /T)$$

也就是说，通过连续点值采样的序列 $x_d[n]$ 的傅里叶变换形状和冲激采样序列 $x_p(t)$ 的傅里叶变换的形状一样，只不过有个时间尺度 $T$ 的缩放（相当于时间归一化），在概念上是完全一致的。

而对于逆过程，是完全一致的，即将离散序列转换成冲激序列，再通入低通滤波器即可。

一般的，我们将数字系统中的离散频率响应记为 $H_d(e^{j\Omega })$ ，那么整个系统可以表示为：

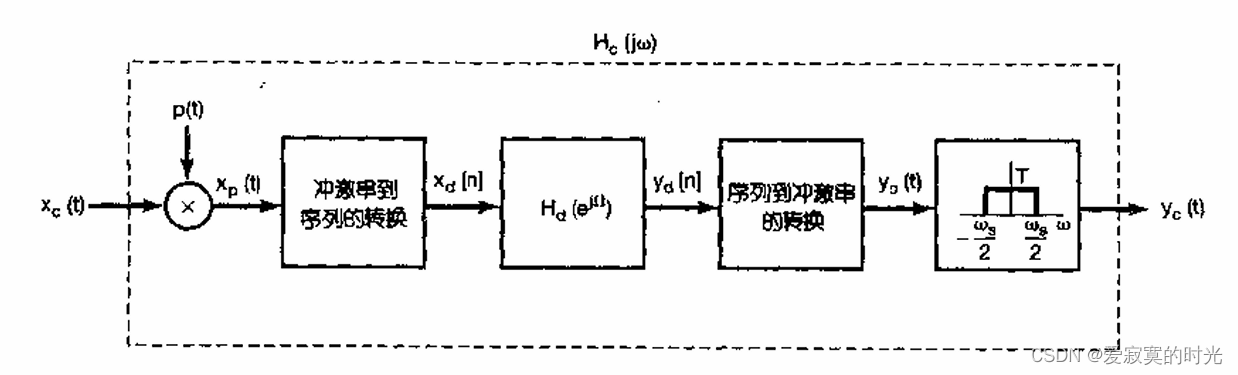
显然：

$$Y_c(j\omega )=X_c(j\omega )H_c(j\omega )$$

其中 $H_c(j\omega )$ 是 $H_d(e^{j\Omega })$ 对应的连续时间系统，那么：

$$Y_c(j\omega )=X_c(j\omega )H_d(e^{j\omega T})$$

并且两个的关系为：

$$H_c(j\omega )=H_d(e^{j\omega T}),|\omega |<{\omega }_s/2$$

离散时间信号采样

类似的对离散时间信号采样，离散时间的采样序列为：

$$p[n]=\sum _{k=-\infty }^{+\infty }\delta [n-kN]$$

那么采样后的信号可以表示为：

$$x_p[n]=x[n],n=kN$$

在时域上 $x_p[n]=x[n]p[n]$ 那么在频域上就有：

$$X_p(e^{j\omega })=\frac{1}{2\pi }{\int }_{2\pi }P(e^{j\theta })X(e^{j(\omega -\theta )})d\theta$$

采样序列 $p[n]$ 的傅里叶变换为：

$$P(e^{j\omega })=\frac{2\pi }{N}\sum _{k=-\infty }^{+\infty }\delta (\omega -k{\omega }_s)$$

那么：

$$X_p(e^{j\omega })=\frac{1}{N}\sum _{k=0}^{N-1}X(e^{j(\omega -k{\omega }_s)})$$

同样的对于离散信号当 ${\omega }_s>2{\omega }_M$ 才能正确采样，被离散低通滤波器还原，否则会发生混叠。相同的，无论是否发生混叠，在采样处的值一直相等。

$$x_r[kN]=x[kN]$$

在实际应用中，离散采样中非采样点的点值为0，为了压缩空间，通常使用压缩采样：

$$x_b[n]=x_p[nN]=x[nN]$$

我们把这样的过程称为 抽取 。

其傅里叶变换为：

$$X_b(e^{j\omega })=\sum _{k=-\infty }^{+\infty }{x}_b[k]e^{-j\omega k}=\sum _{k=-\infty }^{+\infty }{x}_p[kN]e^{-j\omega k}$$

令 $n=kN$ 而且当 $n$ 不是 $N$ 的整数倍的时候 $x_p[n]=0$ ，那么就可以写成：

$$X_b(e^{j\omega })=\sum _{k=-\infty }^{+\infty }{x}_p[k]e^{-j\omega k/N}=X_p(e^{j\omega /N})$$

也就是：

$$X_b(e^{j\omega })=X_p(e^{j\omega /N})$$

所以，压缩时间的效果就是将频率扩大 $N$ 倍。