三角形面积公式用坐标用c语言,通过三个点的坐标求出三角形面积的公式
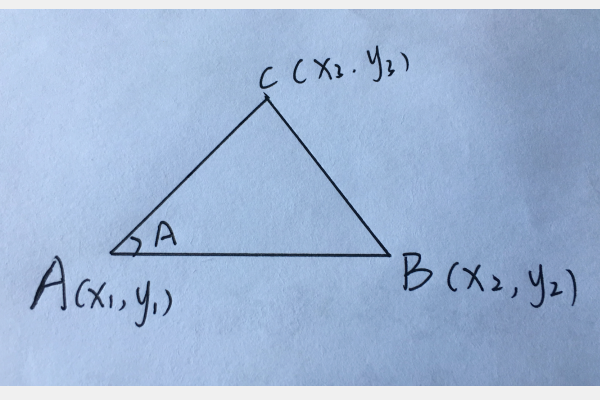
当三个点A、B、C的坐标分别为A(x1,y1)、B(x2,y2)、C(x3、y3)时,三角形面积为,
S=(x1y2-x1y3+x2y3-x2y1+x3y1-x2y2)。
解:设三个点A、B、C的坐标分别为A(x1,y1)、B(x2,y2)、C(x3、y3)。
那么A、B、C三点可围成一个三角形。
AC与AB边的夹角为∠A。
那么向量AB=(x2-x1,y2-y1)、向量AC=(x3-x1,y3-y1)。
令向量AB=a,向量AC=b,
则根据向量运算法则可得,
|a·b|=|a|·|b|·|cosA|,
那么cosA=|a·b|/(|a|·|b|),则sinA=√((|a|·|b|)^2-(|a·b|)^2)/(|a|·|b|)。
那么三角形的面积S=|a|·|b|·sinA=√((|a|·|b|)^2-(|a·b|)^2)
又a·b=(x2-x1)*(x3-x1)+(y2-y1)*(y3-y1),
那么可得三角形的面积S=(x1y2-x1y3+x2y3-x2y1+x3y1-x2y2)。
扩展资料:
1、向量的运算
对于向量a=(x1,y1),b=(x2,y2),c(x3,y3)则向量的运算法则如下。
(1)数量积
对于向量a=(x1,y1),b=(x2,y2),且a,b之间的夹角为A,那么
a·b=b·a、(λa)·b=λ(a·b)、(a+b)·c=a·c+b·c。
a·b=|a|·|b|·cosA,
(2)向量的加法
a+b=b+a、(a+b)+c=a+(b+c)
(3)向量的减法
a+(-b)=a-b
2、正弦定理应用
在任意△ABC中,角A、B、C所对的边长分别为a、b、c,
那么a/sinA=b/sinB=c/sinC。
且三角形面积S=1/2absinC=1/2acsinB=1/2bcsinA。
参考资料来源:百度百科-向量
参考资料来源:百度百科-正弦定理