最优化期末复习

典型题型

判断是否为局部最优解（非线性规划）

1.写出$L(x,w,v)$和$\nabla f(x),\nabla g(x),\nabla h(x)$，求出${\nabla }_{x}L$和${\nabla }_x^{2}L$
（1）判断是否是可行点
（2）找出$I$
（3）根据$I$写出KKT方程。
（4）求解KKT方程，如果$w_i<0$，则不是KKT点->不是局部最优解
（5）如果$w\ge 0$，则是KKT点。写出${\nabla }_x^{2}L$
               \;\;\;\;\;\;\; ①${\nabla }_x^{2}L$正定->在$G$上正定->局部最优解
               \;\;\;\;\;\;\; ②${\nabla }_x^{2}L$不是正定，求$\bar{G}$，如果$\bar{G}=\{(0,0)\}$，则$G=\varnothing$->局部最优解；如果$\bar{G}$还有其他向量且${\nabla }_x^{2}L$在$\bar{G}$上不是半正定的->不是局部最优解

凸集与凸函数

凸集定义和性质～表示定理：《绪论》p60

凸集的定义和性质

定义

超平面 H = { x ∣ p T x = a } H=\{\textbf{x}|\textbf{p}^T\textbf{x}=\textbf{a}\} H={x∣pTx=a}
半空间 H = { x ∣ p T x ≤ a } H=\{\textbf{x}|\textbf{p}^T\textbf{x}\le\textbf{a}\} H={x∣pTx≤a}
射线 L = { x ∣ x = x ( 0 ) + λ d , λ ≥ 0 } L=\{\textbf{x}|\textbf{x}=\textbf{x}^{(0)}+\lambda\textbf{d},\lambda\geq0\} L={x∣x=x(0)+λd,λ≥0}
多面体/集 { x ∣ Ax ≤ b } \{\textbf{x}|\textbf{Ax}\leq\textbf{b}\} {x∣Ax≤b}
{ ∑ i = 1 k λ i α 0 , λ i ≥ 0 } \{\sum_{i=1}^k \lambda_i \alpha^{0}, \lambda_i\geq 0\} {∑i=1k​λi​α0,λi​≥0} 凸集+锥
都是凸集。

性质

$S_1\cup S_2$不一定是凸集

证明是凸集： 1.定义法。 2.性质法，用已知的凸集构造

极点和极方向的定义

极点

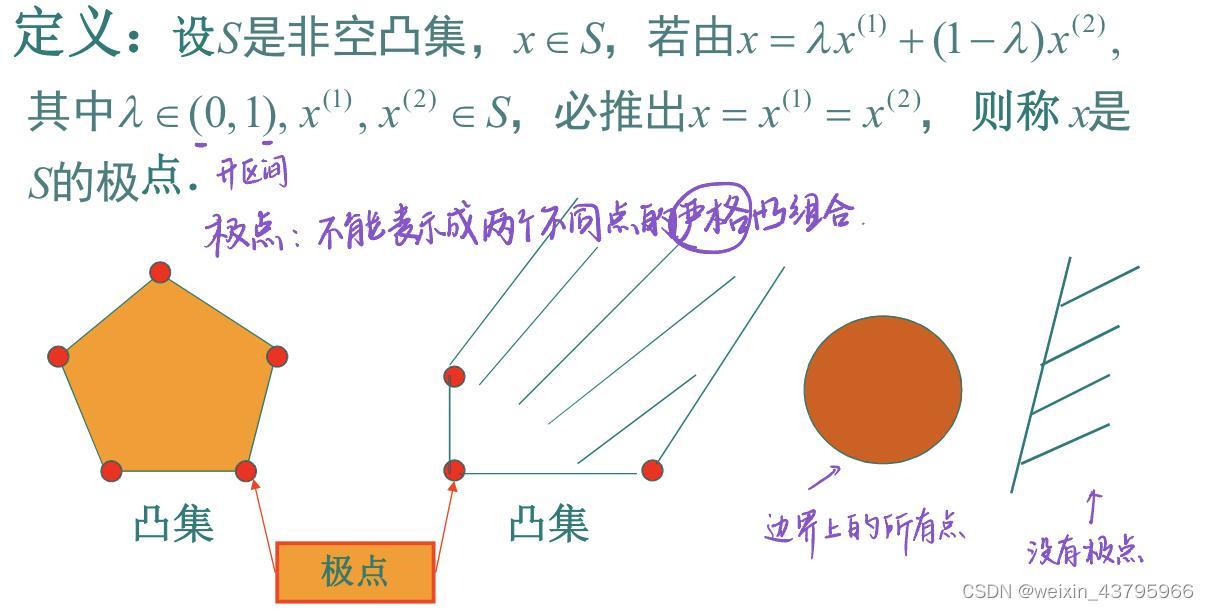
对于紧凸集，任何一点都能被极点的凸组合表示，但是对于无界集不适用->引入极方向。

方向、不同方向、极方向

有界集不存在（极）方向，只有无界集才可能存在。

方向的证明：
1.定义
2.

极方向的证明：
$\text{d}={\alpha }_1{\text{d}}_1+{\alpha }_2{\text{d}}_2$，其中${\alpha }_1,{\alpha }_2>0$，要说明${\text{d}}_1$和${\text{d}}_2$是方向。
如果能推出${\text{d}}_1=\lambda {\text{d}}_2,\lambda >0$，则$\text{d}$是极方向。
证明例子可见《绪论》p65

表示定理

凸集分离定理

定理1：$S$是$E^n$的闭凸集，$y\notin S$，则存在唯一的$\bar{x}\in S$，使得$||y-\bar{x}||=in{f}_{x\in S}||y-x||>0$
$\bar{x}$是这一最小距离点$\leftrightarrow$对任意$x\in S$，有$(y-\bar{x}{)}^T(\bar{x}-x)\ge 0$
定理2：$S$是$E^n$的非空闭凸集，$y\notin S$，则存在非零向量$p$和$ϵ>0$，使得对任意$x\in S$，有$p^{T}y\ge ϵ+p^{T}x$。
定理3：$S$是$E^n$的非空凸集，$y\notin \partial S$，则存在非零向量$p$，使得对任意$x\in clS$，有$p^{T}y\ge p^{T}x$。
推论4：$S$是$E^n$的非空凸集，$y\notin S$，则存在非零向量$p$，使得对任意$x\in clS$，有$p^T(x-y)\le 0$。
定理5：$S_1$和$S_2$是两个非空凸集，$S_1\cap S_2=\varnothing$，则存在非零向量$p$，使得$inf${$p^{T}x|x\in S_1$}$\ge$$sup${$p^{T}x|x\in S_2$}
定理6：$S_1$和$S_2$是两个非空闭凸集，$S_1$有界，且$S_1\cap S_2=\varnothing$，则存在非零向量$p$和$ϵ>0$，使得$inf${$p^{T}x|x\in S_1$}$\ge$$ϵ+sup${$p^{T}x|x\in S_2$}

Farkas定理

《教材》p25

Gordan定理

凸函数

定义

性质

f1 f2凸，max{f1, f2}凸

判别

一阶充要条件

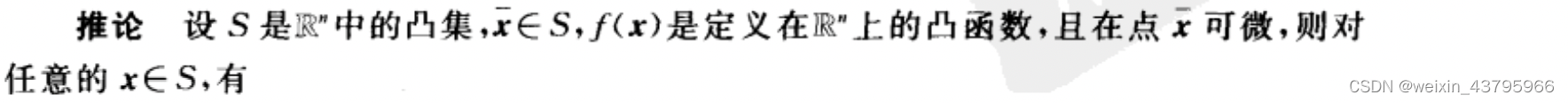
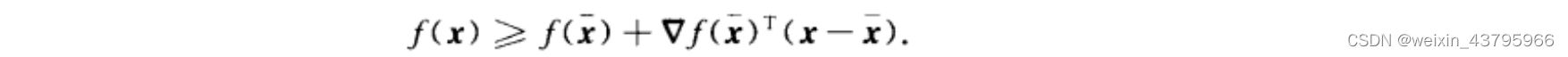
二阶充要条件

逆定理不成立。

凸规划

注意：线性函数既是凸又是凹
凸规划的局部极小点就是全局极小点，且极小点的集合为凸集。

线性规划

非标准型LP转化为标准型LP：
1.$x_j$无非负约束，引入$x_j^{\prime }\ge 0,x_j^{\prime \prime }\ge 0$，令$x_j=x_j^{\prime }-x_j^{\prime \prime }$
2.决策变量有上下界，如$1\le x_3\le 5$，令$x_3^{\prime }=x_3-1$，则$x_3^{\prime }\ge 0,x_3^{\prime }\le 4$，后者可以加一个松弛变量转化为等式
3.含有绝对值
$u_i=\frac{x_i+|x_i|}{2},v_i=\frac{x_i-|x_i|}{2}$，则$u_i,v_i\ge 0,x_i=u_i-v_i,|x_i|=u_i+v_i$

法向量和等值线垂直（$-10x_1-15x_2$的法向量是$(-10,-15{)}^T$），等值线沿着法向量移动时，目标函数值增加；沿法向量反方向移动时，目标函数值减少。

基本概念

无可行解：可行域为空
有可行解：

• 无界解：不存在有限的最优解（认为不存在最优解）
• 有最优解（唯一解/无穷多解）

基本解、基本可行解、（非）退化的基本可行解
A中任意m列组成的m阶可逆方阵B是基（矩阵）。 Ax=b

二阶可逆矩阵：

基本性质

如果LP存在最优解，一定在某个极点上找到。
这些定理的证明可以在《线性规划基本性质》末尾找到
1. K = { x ∣ Ax = b , x ≥ 0 } K=\{\textbf{x}|\textbf{Ax}=\textbf{b},\textbf{x}\geq0\} K={x∣Ax=b,x≥0}的极点集和$\text{Ax}=\text{b},\text{x}\ge 0$的基本可行解等价。
2.可行解$\text{x}$是基本可行解$\iff$ $\text{x}$的非零向量对应的A列向量线性无关
3. S = { x ∣ Ax = b , x ≥ 0 } S=\{\textbf{x}|\textbf{Ax}=\textbf{b},\textbf{x}\geq0\} S={x∣Ax=b,x≥0}的方向$\text{d}$有k个非零分量，则$\text{d}$是$S$的极方向$\iff$ $\text{d}$的非零分量所对应A的列向量组的秩为k-1.
4.(1)LP有可行解，则一定有基本可行解。(2)如果有最优解，则存在一个基本可行解是最优解。
(3)如果有最优解，要么唯一，要么无穷。

单纯形法

极小化问题中，对于某个基本可行解，如果$z_j-c_j=c_B{B}^{-1}{p}_j-c_j\le 0$，或是$c_B{B}^{-1}N-c_N\le 0$

达到最优解时，如果某个非基变量的检验数为零，则该LP存在多个最优解。
注意达到最优解时，y可以任取，但b≥0。

表格形式的单纯形法：

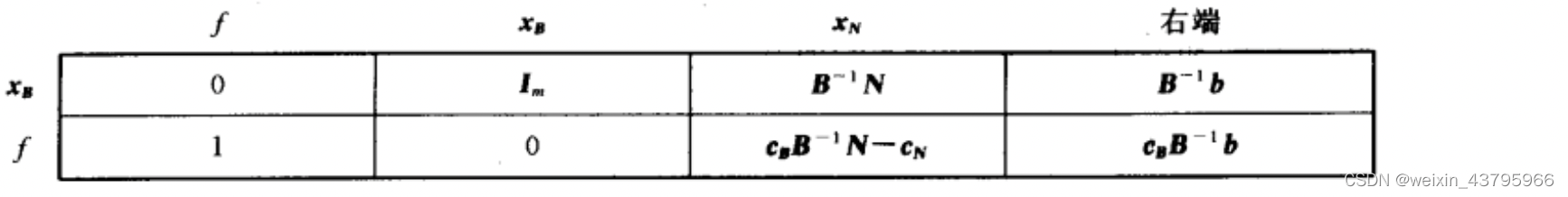
寻找初始可行解：两阶段法/大M法

${\text{x}}_a$是在每一行增加的人工变量（为了凑出一个单位矩阵）。

两阶段法

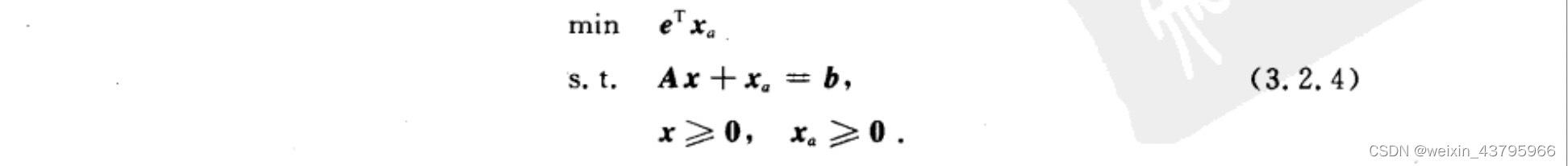
情况（2），删去人工变量所在列，重新计算最后一行。

$y_i=B^{-1}{p}_j,\bar{b}=B^{-1}b$，所以在重新计算时可以直接用$z_j-c_j=c_B{y}_i-c_j,f=c_B\bar{b}$

大M法

退化解：某个基变量=0，可能会造成计算过程的循环。（确定出基变量时如果有多个最小比值，会出现退化解）

对偶原理

不同形式的对偶问题

对称形式

非对称形式

原问题：
$$\begin{gathered} min\text{cx} \\ s.t.\text{Ax}=\text{b} \\ \text{x}\ge \text{0} \end{gathered}$$

对偶问题：
$$\begin{gathered} min\text{wb} \\ s.t.\text{wA}\le \text{c} \end{gathered}$$

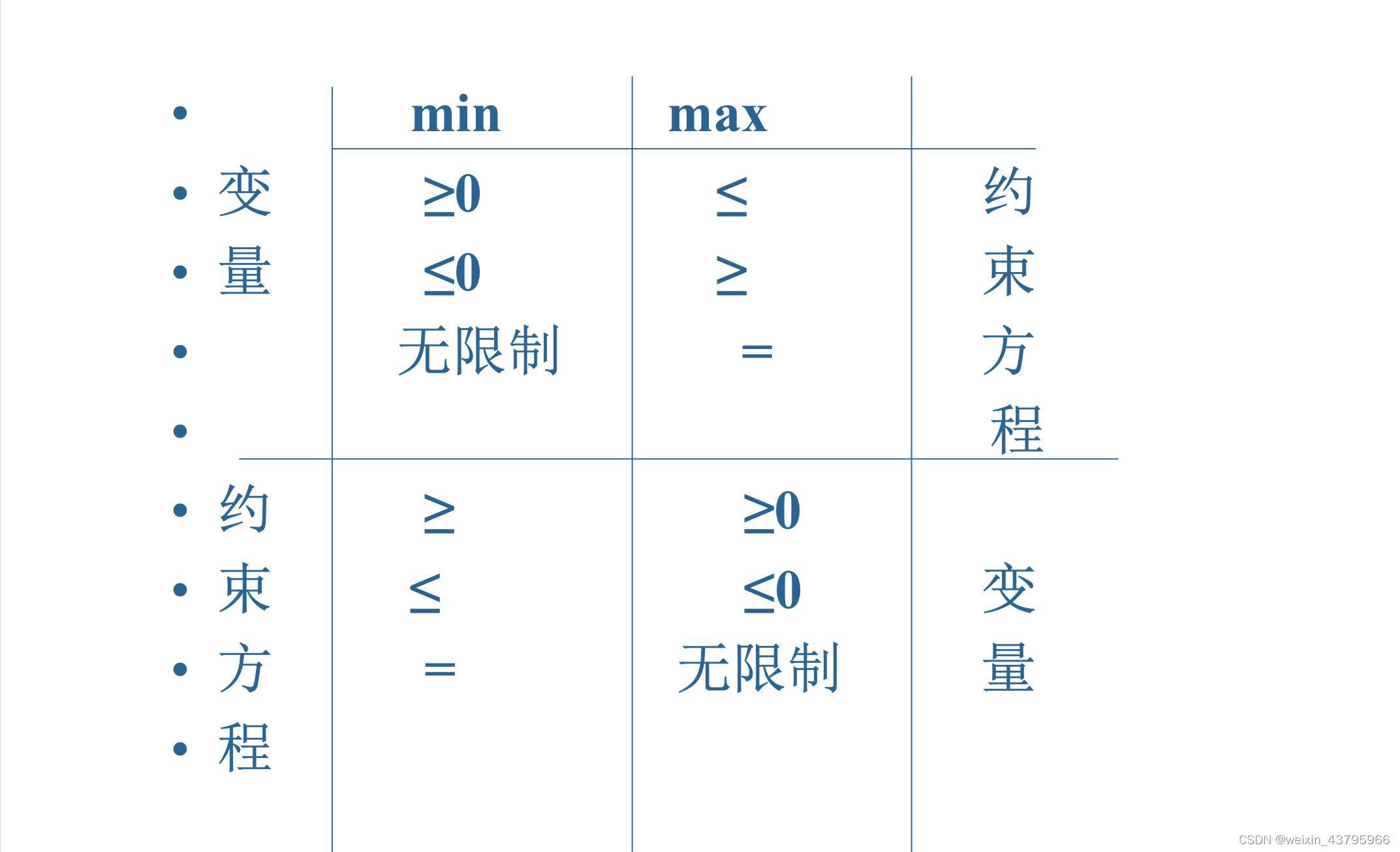
对偶定理

弱对偶定理

${\text{x}}^{(0)}$和${\text{w}}^{(0)}$是可行解，则${\text{cx}}^{(0)}\ge {\text{w}}^{(0)}\text{b}$
推论：
1.若LP（或DLP）问题有无界解，则其对偶问题（或原问题）无可行解；若LP（或DLP）问题有无可行解，则其对偶问题（或原问题）无可行解/目标函数值趋于无穷；
2.极大化问题的任何一个可行解所对应目标函数值都是其对偶问题目标函数值的下界；
3.极小化问题的任何一个可行解所对应目标函数值都是其对偶问题目标函数值的上界。

最优性准则

强对偶定理

若(L)(D)均有可行解 -> (L)(D)均有最优解->(L)(D)的最优目标函数值相等。
推论：若原问题（对偶问题）有最优解，则 对偶问题（原问题）也有最优解，且最优目标函数值相等。

互补松弛定理

（对称形式）

（非对称形式）

对偶单纯形法

如何得到初始对偶可行的基本解？


然后继续用对偶单纯形法解扩充问题
（1）扩充问题无解->原问题无解
（2）扩充问题有最优解->得到原问题可行解，如果扩充问题的最优值与M无关，则也是原问题的最优解
例子在《教材》p150

灵敏度分析

价格系数改变

非基变量

$x_k$的系数从$c_k$变为$c_k^{\prime }$：
若$j\ne k,z_j^{\prime }-c_j^{\prime }=z_j-c_j$不变
若$j=k,z_k^{\prime }-c_k^{\prime }=z_k-c_k-(c_k^{\prime }-c_k)$
如果$z_k^{\prime }-c_k^{\prime }\le 0$，B仍为最优基，反之$x_k$为进基变量。

基变量

若$j\ne k,z_j^{\prime }-c_j^{\prime }=z_j-c_j+(c_k^{\prime }-c_k)y_{kj}$
若$j=k,z_k^{\prime }-c_k^{\prime }=0$
将原单纯形表$x_k$所在航乘$(c_k^{\prime }-c_k)$到判别数行，并将$x_k$对应判别数设为0.

右端向量改变

1.$B^{-1}{b}^{\prime }\ge 0$，原来的最优基仍为最优基，但基变量取值、目标函数最优值都会变化

$x_B^{\prime }=B^{-1}{b}^{\prime }=B^{-1}b+B^{-1}\Delta b$
$x_N^{\prime }=0$
$f_{min}^{\prime }=f_{min}+c_B{B}^{-1}\Delta b$

2.$B^{-1}{b}^{\prime }$不是所有分量都大于等于0
原来的最优基不再可行，但是是对偶可行的基本解，重新求解。
将最右一列修改为$[B^{-1}{b}^{\prime },c_B{B}^{-1}b{]}^T$即可。

增加新约束

$P^{m+1}x\le b_{m+1}，P^{m+1}$是n维向量
1.如果原最优解满足新约束，那它也是新问题最优解
2.如果不满足，新约束中引入松弛变量变成等式，然后将系数直接加在表中（松弛变量作为基变量），判别数行不变，新的松弛变量判别数为0。然后高斯方法将基变量的矩阵重新变成单位矩阵->对偶单纯形法。
《教材》p166

最优性条件

主要考虑非线性问题
非线性问题的最优解（如果存在），可在可行域内任意一点达到，但线性规划通常在边界取到。
$\nabla f(x^{\ast })=0$，称$x^{\ast }$为驻点，分为极值点和鞍点。

无约束问题的极值条件

必要条件

一般用来反推某点不是极小点。

一阶

二阶

充分条件

推论：
$f(x)=\frac{1}{2}{x}^{T}Ax+b^{T}x+c$，$A$对称正定，有唯一极小点$x^{\ast }=-A^{-1}b$

充要条件

注意前提：凸函数！

约束极值问题的最优性条件

一些基础概念

下降方向

可行方向

如果是局部极小点，$F_0\cap D=\varnothing$

局部约束方向锥

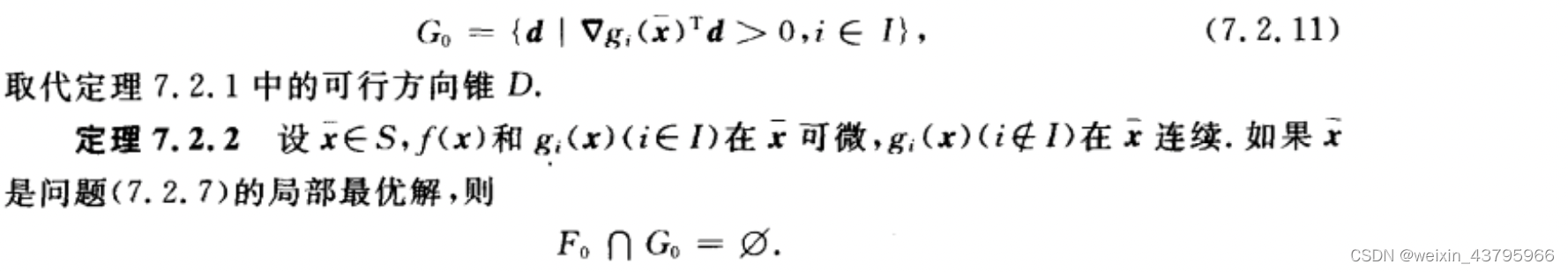
如果$\nabla f(x{)}^{T}d<0,\nabla g_i(x{)}^{T}d>0(i\in I)$，则d是可行下降方向。

正则点

切锥

不等式约束问题的一阶最优性条件

KKT必要条件

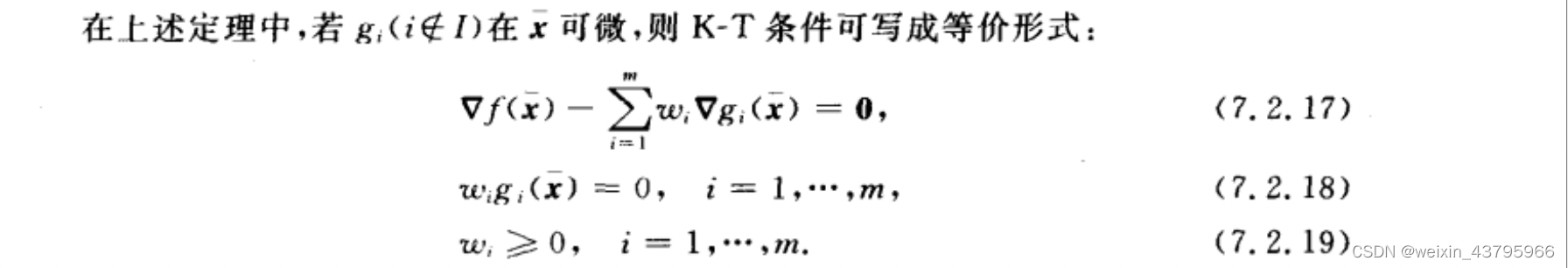
一阶充分条件

凸规划+KKT->整体极小点
推论：如果是凸规划，整体最优解<->KKT点

一般约束问题的一阶最优性条件

KKT必要条件

互补松弛版本：

如果约束都是线性/只有一个约束，一般都是正则点。

Lagrange版本KKT条件

向量版本的Lagrange函数：

一阶充分条件

凸规划+KKT->整体极小点

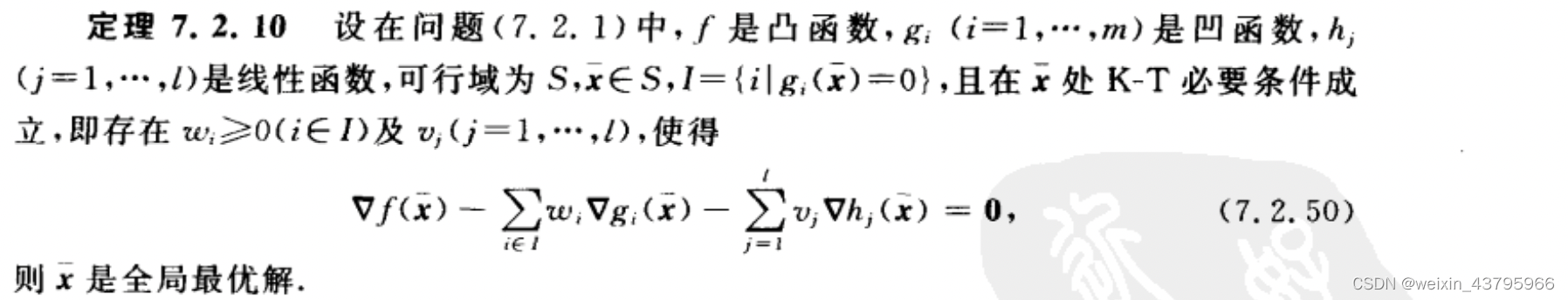
推论：凸（线性）规划，KKT<->最优解

二阶条件

必要

充分

对偶问题

在课件《最优性条件》p111开始

Lagrange对偶问题

如果$\theta (w,v)$不存在有限下界时，令$\theta (w,v)=0$
注意选择不同的集约束，结果可能不同。

对偶定理

弱对偶定理及推论

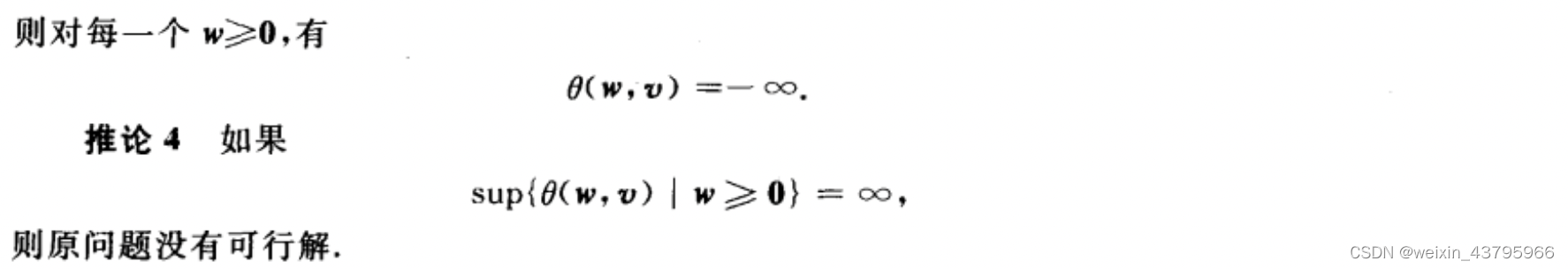
记 f m i n = i n f { f } , θ m a x = s u p { θ } f_{min}=inf\{f\},\theta_{max} = sup\{\theta\} fmin​=inf{f},θmax​=sup{θ}，对偶间隙$\delta =f_{min}-{\theta }_{max}$。

引理

证明见《教材》p245

算法

闭映射

$x^{(k)}$是定义好的点列，每一个$x_i$被映射到$A(x_i)$中，然后$y_i$从集合$A(x_i)$中任取，最终构成了$y^{(k)}$。

二次终止性

对于任意正定二次函数，从任意初始点出发，能经过有限步迭代到达极小值点，则称该算法有二次终止性。

一维搜索

如果$x^{(k+1)}$是由精确一维搜索得到的，则有$\nabla f(x^{(k+1)}{)}^T{d}^k=0$

算法	优点	缺点
0.618法	不要求函数可微，甚至函数不连续时仍可应用	收敛满，只适用于单峰区间，所以需要先确定单峰区间，再使用0.618法的计算公式
牛顿法		初始点很重要，如果靠近极小点，至少以二级收敛速度收敛，但如果距离很远，可能会不收敛
抛物线法	不用求导，计算比较简单	没有牛顿法快，大概1.3
三次插值法

使用导数的最优化方法

最速下降法

最速下降方向：$d^{(k)}=-\nabla f(x^{(k)})$
步长：精确搜索
全局收敛

牛顿法

牛顿方向：$d^{(k)}=-{\nabla }^{2}f(x^{(k)}{)}^{-1}\nabla f(x^{(k)})$，不一定是下降方向。
步长：恒为1
可能收敛到极小点/鞍点，也可能Hesse矩阵不可逆无法继续迭代

阻尼牛顿法：步长为1 -> 精确搜索
修正牛顿法：保证每一步迭代目标函数值都下降

算法	优点	缺点	二次终止性
最速下降法	全局收敛。初始点任取。迭代过程简单，计算量和存储量小，开始时函数值下降很快，可以快速靠近最优解	收敛速度慢，强条件下仅为线性。相邻两搜索方向正交，不适用于算法收局。	无
牛顿法	收敛速度快（至少二阶）	初始点不能任取。某步迭代时函数值可能上升。可能会不收敛/收敛到鞍点/无法计算。计算量存储量大	有
共轭梯度法	初始点任取，计算量和存储量小，线性收敛		有

共轭方向法

《使用导数的最优化方法》p35

共轭方向

扩张子空间定理

共轭方向法

共轭梯度法

可行方向法

Zoutendijk可行方向法

求可行下降方向

非线性约束的情形 p25

Rosen梯度投影法

正交投影矩阵

梯度投影法原理

Wolfe既约梯度法

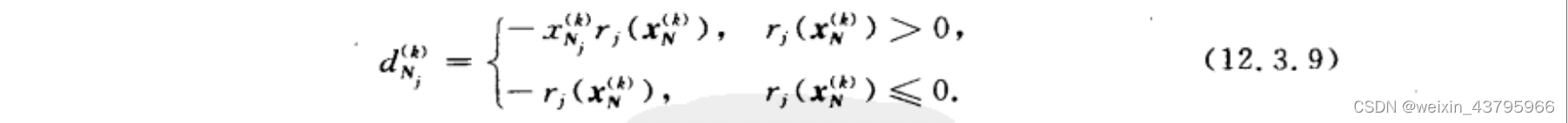
惩罚函数法

将约束函数揉进目标函数，从而将约束优化转化为与原问题近似的无约束优化。

外点法

方法	优点	缺点	特点
外点法	初始点可以任取，可用于非凸规划的最优化	惩罚项的二阶偏导数一般不存在；外点法的中间结果不是可行解，不可作为近似解；xk接近最优解时，罚因子可能很大，使罚函数性质变化，使搜索产生极大困难。	惩罚系数不断增大
内点法	中间结果都是可行解，可作为近似解	选取初始点很困难，只适用于含不等式的非线性规划	惩罚系数不断缩小

内点法

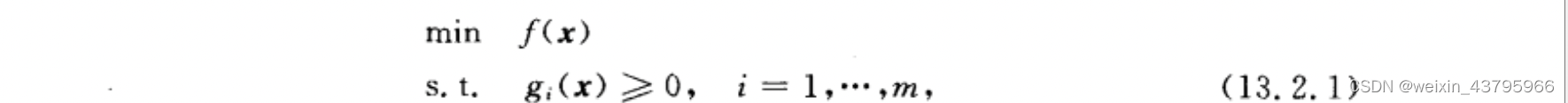
i n t    S = { s ∣ g i ( x ) > 0 , i = 1 , 2 , . . . , m } int\;S=\{s|g_i(x)>0,i=1,2,...,m\} intS={s∣gi​(x)>0,i=1,2,...,m}