【数据结构--哈夫曼编码(C语言版)】
哈夫曼树及其应用
哈夫曼树
介绍哈夫曼树前先介绍下面几个名词:
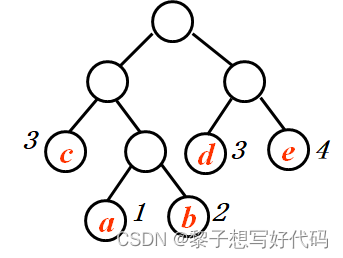
1. 结点的路径长度l
从根结点到该结点的路径上分支的数目,如下图结点a的l = 3。
2. 树的路径长度
树中所有叶子结点的路径长度之和,如下图该树的路径长度为2 + 3 + 3 + 2 + 2。
3. 结点的权w
给每一个结点赋予一个新的数值,称为这个结点的权。
4. 结点的带权路径长度l * w
从根结点到该结点之间的路径长度与该结点的权的乘积,下图结点a的带权路径长度为l * w = 3。
5. 树的带权路径长度 WPL = ∑li * wi
树中所有叶子结点的带权路径长度之和。
带权路径长度WPL最小的二叉树称为哈夫曼树(又称为最优二叉树)。
哈夫曼树的特点
- 权值小的结点离根远,权值大的结点离根近。
- 结点的度:没有度为1的结点。
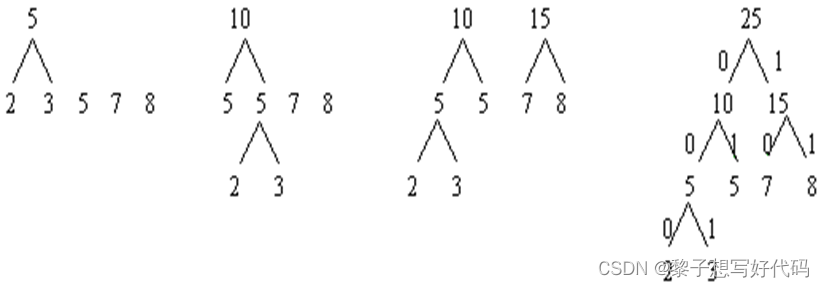
哈夫曼树的构造
思路:
1. 对于给定的有各自权值的n个结点,从n个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新的二叉树的根结点的权值为左右孩子权值的和
2. 在原有的n个权值中删除那两个最小的权值,同时将新的权值加入到n-2个权值的行列中,以此类推
3. 重复1和2,直到所有的结点构建成了一棵二叉树为止,该树即为哈夫曼树。
哈夫曼编码
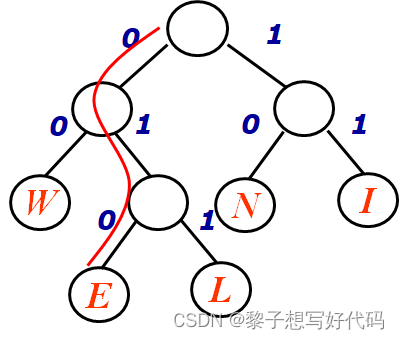
一般地,设需要编码的字符集为{d1, d2, …… ,dn},各个字符在电文中出现的次数或频率集合为{w1, w2, …… , wn},以d1,d2,…… ,dn作为叶子结点,以w1,w2,…… ,wn作为相应叶子结点的权值来构造一棵哈夫曼树。规定哈夫曼树的左分支代表0,右分支代表1,则从根结点到叶子结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码,这就是哈夫曼编码。
例如有一段文字内容"WINNIE WILL WIN"其中W的权值为3,I的权值为4,N的权值为3,E的权值为1,L的权值为2 ,则其按哈夫曼树规划如下。
| W | I | N | E | L |
|---|---|---|---|---|
| 3 | 4 | 3 | 1 | 2 |
| 00 | 11 | 10 | 010 | 011 |
- 构造以
W(3)、I(4)、N(3)、E(1)、L(2)为叶子结点的哈夫曼树 - 将该二叉树所有左分枝标记
0,所有右分枝标记1 - 根结点到叶子结点所经过的二进制序列为该叶子结点字符的编码
哈夫曼树结构
/* 哈夫曼树结构 */
typedef struct HTree
{
char data;
int weight;
int parent,leftChild,rightChild;
} HTNode, *HuffmanTree;
编码结构
/* 编码结构 */
typedef struct HCode
{
char data;
char* str;
} *HuffmanCode, HCode;
统计字符和对应的次数
/* 统计字符和对应的次数 */
typedef struct wordcnt
{
char ch;
int cnt = 0;
} Count;
/* 统计次数的外部封装 */
typedef struct NumCount
{
Count count[MAXSIZE];
int length = 0;
} NumCount;
读入文件
/* 读入文件 */
Status ReadData(char* source)
{
char ch;
int i=0;
FILE* pFile;
pFile = fopen("myfile.txt","r");
printf("正在读取文件\n");
ch = fgetc(pFile);
if(ch == EOF)
{
printf("文件为空\n");
fclose(pFile);
return ERROR;
}
fclose(pFile);
pFile = fopen("myfile.txt","r");
printf("文件内容是:");
while ((ch = fgetc(pFile)) != EOF)
{
source[i++] = ch;
}
source[i] = '\0';
printf("%s\n",source);
fclose(pFile);
return OK;
}
统计次数
/* 统计次数 */
Status WordCount(char* data, NumCount* tempCnt)
{
int flag; //判断是否已经记录
int len = strlen(data);
for(int i = 0; i < len; ++i)
{
flag = 0;
for(int j = 0; j < tempCnt->length; ++j)
{
if(tempCnt->count[j].ch == data[i]) //若已有记录,直接++
{
++tempCnt->count[j].cnt;
flag = 1;
break;
}
}
if(!flag) //若未记录,则新增
{
tempCnt->count[tempCnt->length].ch = data[i];
++tempCnt->count[tempCnt->length].cnt;
++tempCnt->length;
}
}
return OK;
}
展示次数
/* 展示次数 */
Status Show(NumCount* tempCnt)
{
printf("长度为%d\n",tempCnt->length);
for(int i = 0; i < tempCnt->length; ++i)
{
printf("字符%c出现%d次\n",tempCnt->count[i].ch,tempCnt->count[i].cnt);
}
printf("\n");
return OK;
}
选中权值最小的两个结点
/* 选中权重最小的两个结点 */
Status select(HuffmanTree HT, int top, int* s1, int* s2)
{
int min = INT_MAX;
for(int i = 1; i <= top; ++i) //选择没有双亲的结点中,权重最小的结点
{
if(HT[i].weight < min && HT[i].parent == 0)
{
min = HT[i].weight;
*s1 = i;
}
}
min = INT_MAX;
for (int i = 0; i <= top; ++i) //选择没有双亲的结点中,权重次小的结点
{
if(HT[i].weight < min && i != *s1 && HT[i].parent ==0)
{
min = HT[i].weight;
*s2 = i;
}
}
return OK;
}
创建哈夫曼树
/* 创建哈夫曼树 */
Status CreateHuffmanTree(HuffmanTree &HT, int length, NumCount cntarray)
{
if(length <= 1)
return ERROR;
int s1,s2;
int m = length * 2 - 1; //没有度为1的结点,则总结点数是2 * 叶子结点数 - 1个
HT = (HuffmanTree)malloc(sizeof(HTNode) * (m + 1));
for (int i = 1; i <= m; ++i) //初始化
{
HT[i].parent = 0;
HT[i].leftChild = 0;
HT[i].rightChild = 0;
}
for(int i = 1; i <= length; ++i)
{
HT[i].data = cntarray.count[i-1].ch;
HT[i].weight = cntarray.count[i-1].cnt;
}
for(int i = length + 1; i <= m; ++i)
{
select(HT, i - 1, &s1, &s2); //从前面的范围里选中权重最小的两个结点
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].leftChild = s1;
HT[i].rightChild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight; //得到一个新结点
}
return OK;
}
创建哈夫曼编码
/* 创建哈夫曼编码 */
Status CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int length)
{
HC = (HuffmanCode)malloc(sizeof(HCode) * (length + 1));
char* cd = (char*)malloc(sizeof(char) * length); //存储代码的临时空间
cd[length-1] = '\0'; //方便之后调用strcpy函数
int c,f,start;
for(int i = 1; i <= length; ++i)
{
start = length-1; //start表示编码在临时空间内的起始下标,由于是从叶子节点回溯,所以是从最后开始
c = i;
f = HT[c].parent;
while (f != 0)
{
--start; //由于是回溯,所以从临时空间的最后往回计
if(HT[f].leftChild == c)
cd[start] = '0';
else
cd[start] = '1';
c = f;
f = HT[c].parent;
}
HC[i].str = (char*)malloc(sizeof(char) * (length - start)); // 最后,实际使用的编码空间大小是length-start
HC[i].data = HT[i].data;
strcpy(HC[i].str, &cd[start]); // 从实际起始地址开始,拷贝到编码结构中
}
free(cd);
}
将读入的文件编码写入txt文件
/* 将读入的文件编码,写到txt文件 */
Status Encode(char* data, HuffmanCode HC, int length)
{
FILE* pFile;
pFile = fopen("mycode.txt","w");
for(int i = 0; i < strlen(data); ++i) //依次读入数据,查找对应的编码,写入编码文件
{
for(int j = 1; j <= length; ++j)
{
if(data[i] == HC[j].data)
{
fputs(HC[j].str,pFile);
}
}
}
fclose(pFile);
printf("编码文件已写入\n");
return OK;
}
解码
/* 读入编码文件,解码 */
Status Decode(HuffmanTree HT,int length)
{
char* codetxt = (char*)malloc(sizeof(char)*(MAXSIZE*length));
FILE* pFile;
pFile = fopen("mycode.txt","r");
fgets(codetxt, MAXSIZE*length, pFile);
fclose(pFile);
FILE* outfile;
outfile = fopen("mytxt.txt","w");
int root = 2*length - 1; //从根结点开始遍历
for(int i = 0; i < strlen(codetxt); ++i)
{
if(codetxt[i] == '0')
root = HT[root].leftChild; //为0表示向左遍历
else if(codetxt[i] == '1')
root = HT[root].rightChild; //为1表示向右遍历
if(HT[root].leftChild == 0 && HT[root].rightChild ==0) //如果已经是叶子结点,输出到文件中,然后重新返回到根结点
{
putc(HT[root].data,outfile);
root = 2*length-1;
}
}
fclose(outfile);
printf("输出文件已写入\n");
return OK;
}
完整代码
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAXSIZE 1024 // 读入文件的上限
#define OK 1
#define ERROR 0
typedef int Status;
/* 统计字符和对应的次数 */
typedef struct wordcnt
{
char ch;
int cnt = 0;
} Count;
/* 统计次数的外部封装 */
typedef struct NumCount
{
Count count[MAXSIZE];
int length = 0;
} NumCount;
/* 哈夫曼树结构 */
typedef struct HTree
{
char data;
int weight;
int parent,leftChild,rightChild;
} HTNode, *HuffmanTree;
/* 编码结构 */
typedef struct HCode
{
char data;
char* str;
} *HuffmanCode, HCode;
/* 读入文件 */
Status ReadData(char* source)
{
char ch;
int i=0;
FILE* pFile;
pFile = fopen("myfile.txt","r");
printf("正在读取文件\n");
ch = fgetc(pFile);
if(ch == EOF)
{
printf("文件为空\n");
fclose(pFile);
return ERROR;
}
fclose(pFile);
pFile = fopen("myfile.txt","r");
printf("文件内容是:");
while ((ch = fgetc(pFile)) != EOF)
{
source[i++] = ch;
}
source[i] = '\0';
printf("%s\n",source);
fclose(pFile);
return OK;
}
/* 统计次数 */
Status WordCount(char* data, NumCount* tempCnt)
{
int flag; //判断是否已经记录
int len = strlen(data);
for(int i = 0; i < len; ++i)
{
flag = 0;
for(int j = 0; j < tempCnt->length; ++j)
{
if(tempCnt->count[j].ch == data[i]) //若已有记录,直接++
{
++tempCnt->count[j].cnt;
flag = 1;
break;
}
}
if(!flag) //若未记录,则新增
{
tempCnt->count[tempCnt->length].ch = data[i];
++tempCnt->count[tempCnt->length].cnt;
++tempCnt->length;
}
}
return OK;
}
/* 展示次数 */
Status Show(NumCount* tempCnt)
{
printf("长度为%d\n",tempCnt->length);
for(int i = 0; i < tempCnt->length; ++i)
{
printf("字符%c出现%d次\n",tempCnt->count[i].ch,tempCnt->count[i].cnt);
}
printf("\n");
return OK;
}
/* 选中权重最小的两个结点 */
Status select(HuffmanTree HT, int top, int* s1, int* s2)
{
int min = INT_MAX;
for(int i = 1; i <= top; ++i) //选择没有双亲的结点中,权重最小的结点
{
if(HT[i].weight < min && HT[i].parent == 0)
{
min = HT[i].weight;
*s1 = i;
}
}
min = INT_MAX;
for (int i = 0; i <= top; ++i) //选择没有双亲的结点中,权重次小的结点
{
if(HT[i].weight < min && i != *s1 && HT[i].parent ==0)
{
min = HT[i].weight;
*s2 = i;
}
}
return OK;
}
/* 创建哈夫曼树 */
Status CreateHuffmanTree(HuffmanTree &HT, int length, NumCount cntarray)
{
if(length <= 1)
return ERROR;
int s1,s2;
int m = length * 2 - 1; //没有度为1的结点,则总结点数是2 * 叶子结点数 - 1个
HT = (HuffmanTree)malloc(sizeof(HTNode) * (m + 1));
for (int i = 1; i <= m; ++i) //初始化
{
HT[i].parent = 0;
HT[i].leftChild = 0;
HT[i].rightChild = 0;
}
for(int i = 1; i <= length; ++i)
{
HT[i].data = cntarray.count[i-1].ch;
HT[i].weight = cntarray.count[i-1].cnt;
}
for(int i = length + 1; i <= m; ++i)
{
select(HT, i - 1, &s1, &s2); //从前面的范围里选中权重最小的两个结点
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].leftChild = s1;
HT[i].rightChild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight; //得到一个新结点
}
return OK;
}
/* 创建哈夫曼编码 */
Status CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int length)
{
HC = (HuffmanCode)malloc(sizeof(HCode) * (length + 1));
char* cd = (char*)malloc(sizeof(char) * length); //存储代码的临时空间
cd[length-1] = '\0'; //方便之后调用strcpy函数
int c,f,start;
for(int i = 1; i <= length; ++i)
{
start = length-1; //start表示编码在临时空间内的起始下标,由于是从叶子节点回溯,所以是从最后开始
c = i;
f = HT[c].parent;
while (f != 0)
{
--start; //由于是回溯,所以从临时空间的最后往回计
if(HT[f].leftChild == c)
cd[start] = '0';
else
cd[start] = '1';
c = f;
f = HT[c].parent;
}
HC[i].str = (char*)malloc(sizeof(char) * (length - start)); // 最后,实际使用的编码空间大小是length-start
HC[i].data = HT[i].data;
strcpy(HC[i].str, &cd[start]); // 从实际起始地址开始,拷贝到编码结构中
}
free(cd);
}
/* 将读入的文件编码,写到txt文件 */
Status Encode(char* data, HuffmanCode HC, int length)
{
FILE* pFile;
pFile = fopen("mycode.txt","w");
for(int i = 0; i < strlen(data); ++i) //依次读入数据,查找对应的编码,写入编码文件
{
for(int j = 1; j <= length; ++j)
{
if(data[i] == HC[j].data)
{
fputs(HC[j].str,pFile);
}
}
}
fclose(pFile);
printf("编码文件已写入\n");
return OK;
}
/* 读入编码文件,解码 */
Status Decode(HuffmanTree HT,int length)
{
char* codetxt = (char*)malloc(sizeof(char)*(MAXSIZE*length));
FILE* pFile;
pFile = fopen("mycode.txt","r");
fgets(codetxt, MAXSIZE*length, pFile);
fclose(pFile);
FILE* outfile;
outfile = fopen("mytxt.txt","w");
int root = 2*length - 1; //从根结点开始遍历
for(int i = 0; i < strlen(codetxt); ++i)
{
if(codetxt[i] == '0')
root = HT[root].leftChild; //为0表示向左遍历
else if(codetxt[i] == '1')
root = HT[root].rightChild; //为1表示向右遍历
if(HT[root].leftChild == 0 && HT[root].rightChild ==0) //如果已经是叶子结点,输出到文件中,然后重新返回到根结点
{
putc(HT[root].data,outfile);
root = 2*length-1;
}
}
fclose(outfile);
printf("输出文件已写入\n");
return OK;
}
/* 测试 */
void test()
{
char data[MAXSIZE];
NumCount Cntarray;
ReadData(data); //读入数据
WordCount(data, &Cntarray); //统计次数
//Show(&Cntarray); //查看每个单词出现的次数
HuffmanTree tree;
CreateHuffmanTree(tree, Cntarray.length, Cntarray); //建树
HuffmanCode code;
CreateHuffmanCode(tree, code, Cntarray.length); //创建编码
Encode(data, code, Cntarray.length); //生成编码文件
Decode(tree, Cntarray.length); //解码
printf("请查看生成的TXT文件以检查结果\n");
return ;
}
int main()
{
test();
return 0;
}
测试结果
正在读取文件
文件内容是:In love folly is always sweet
I love three things in this world. Sun, moon and you. Sun for morning, moon for night , and you forever .
"In fact, I am very satisfied at least know your name heard your voice to see your eyes."
The furthest distance in the world. Is not being apart while being in love. But when plainly cannot resist the yearning. Yet pretending you have never been in my heart.
编码文件已写入
输出文件已写入
请查看生成的TXT文件以检查结果