详细讲解半加器、全加器、四位全加器，并使用FPGA实现半加器、全加器

全加器、半加器都是在数电学习路上非常主要的部分，下面我将全加器和半加器做一个详细的解释。

半加器

半加器是指对输入的两个一位二进制数相加（A与B），输出一个结果位（SUM）和进位（C），没有进位的输入加法器电路，是一个实现一位二进制数的加法电路。

真值表

被加数A	加数B	和SUM	进位C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

逻辑表达式

根据上述的真值表，当A和B相同时SUM为0，否则为1；逻辑关系属于异或；当A和B同时为1时，C等于1，其余都为零，逻辑关系为与。
所以我们可以得到如下的逻辑表达式：

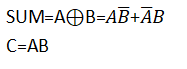
逻辑电路图

半加器Verilog代码实现

module half adder(
	input wire A,
	input wire B,
	output wire C,
	output wire sum
);

//assign sum = (A == B) ? 0 : 1;  //这两种方式都可以实现
assign sum = A^B;
assign C= A&B;

endmodule 

RTL视图验证

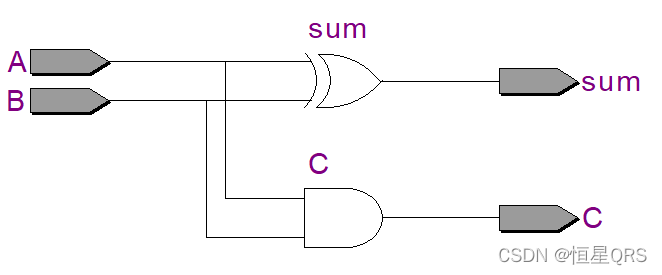
全加器

全加器是指对输入的两个二进制数相加（A与B）同时会输入一个低位传来的进位（Ci-1），得到和数（SUM）和进位（Ci）；一位全加器可以处理低位进位，并输出本位加法进位。多个一位全加器进行级联可以得到多位全加器。常用二进制四位全加器74LS283。

真值表

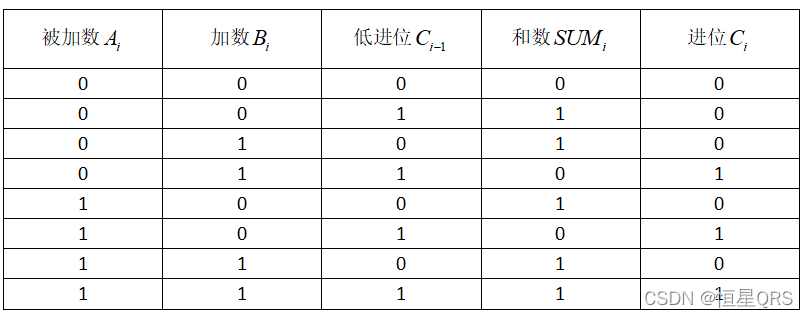
逻辑表达式

由全加器的定义理解我们可以知道当Ai和Bi异或后再与Ci-1进行异或得到SUMi，结合真值表，我们可以知道当Ai、Bi、Ci-1只要有两个以上的1是进位Ci就等于1；所以只需要每两变量求与，结果再求或就可以满足要求。由此我们可以得到最常用的逻辑表达式：

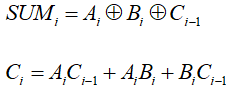
由于两个半加器可以构成一个全加器，所以在这里进位Ci还可以表示为

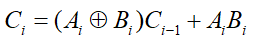
逻辑电路图

根据逻辑表达式绘制两种逻辑电路图如下：

由两个半加器组成的全加器逻辑电路图

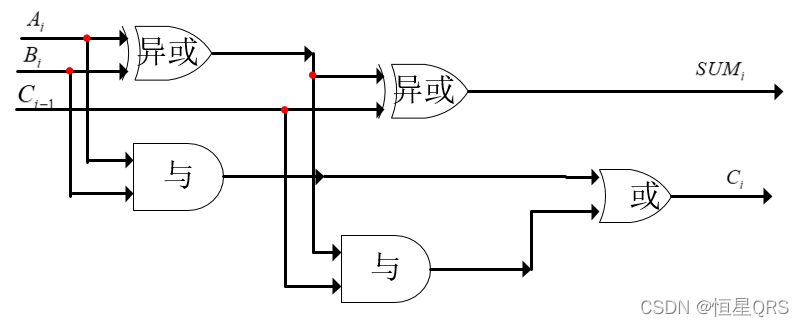
全加器Verilog代码实现

module full_adder(
input wire A,
input wire B,
output wire C,
output wire sum
);

wire sum_h1;
wire count_h1;
wire count_h2;

half_adder half_adder1(
.A(A),
.B(B),
.sum(sum_h1),
.C(count_h1)
);

half_adder half_adder2(
.A(sum_h1),
.B(cin),
.sum(sum),
.C(count_h2)
);
assign C = count_h1 | count_h2;
endmodule

RTL视图验证

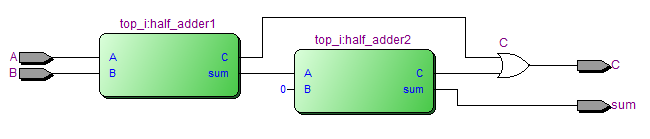
四位全加器

四位全加器的典型代表为74LS283，接下来主要通过真值表和逻辑电路图研究其工作原理。

真值表

我们输入一个二进制数，假设得到的四位二进制数的每一位分别是a、b、c、d，其中a是第一位，举例 a=0；b=0；c=1；d=1；那么这个数为0011；由此我们真值表如下：

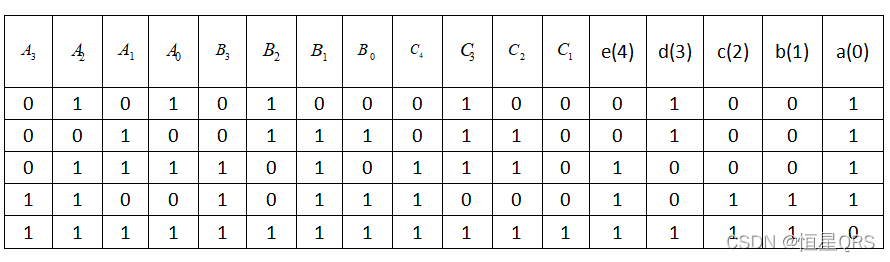
我们列举部分；大家可以计算下其他数值的情况。在这里由于第一位的上级进位都是0，所以省略，后三种数值由于溢出，我们在这里为了方便观察，所以进行了补位，实际情况中是没有第5位（e4）的：

逻辑电路图

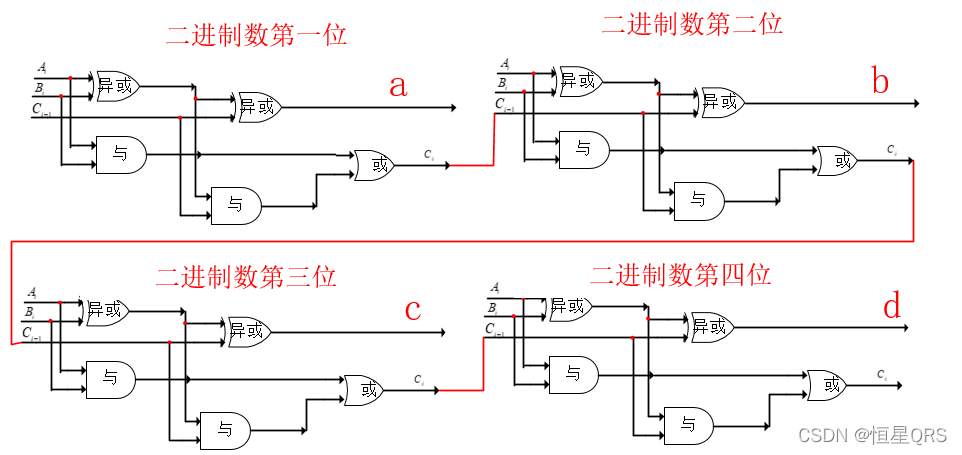
今天的讲解就到这里了，如果有问题，请留言联系我。