MATLAB作图

1.曲线图

MATLAB作图是通过描点、连线来实现的，故在画一个曲线图形之前，必须先取得该图形上的一系列的点的坐标（即横坐标和纵坐标），然后将该点集的坐标传给MATLAB函数画图.

命令为： plot(X,Y,S)

X,Y是向量,分别表示点集的横坐标和纵坐标

S（线型）：y 黄色 . 点 - 连线 m 洋红 o 圈 : 短虚线 c 蓝绿色 x x-符号 -. 长短线 r 红色 + 加号 -- 长虚线

plot(X,Y) — 画实线

plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn) — 将多条线画在一起

例在[0,2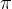 $\pi$ ]用红线画sin x,用绿圈画cos x.

x=linspace(0,2*pi,30);
y=sin(x);
z=cos(x);
plot(x,y,'r',x,z, 'g0')

2.符号函数(显函数、隐函数和参数方程)画图

(1) ezplot

ezplot(‘f(x)’,[a,b]): 表示在a<x<b绘制显函数f=f(x)的函数图.

ezplot(‘f(x,y)’,[xmin,xmax,ymin,ymax]): 表示在区间xmin<x<xmax和 ymin<y<ymax绘制隐函数f(x,y)=0的函数图.

ezplot(‘x(t)’,’y(t)’,[tmin,tmax]): 表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图.

例在[0, 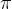$\pi$ ]上画y=cos x 的图形.

ezplot(‘sin(x)’,[0,pi])

例在[-2，0.5]，[0，2]上画隐函数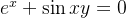 $e^{x}+\sin xy=0$ 的图.

ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])

(2) fplot

fplot(‘fun’,lims): 表示绘制字符串fun指定的函数在lims=[xmin,xmax]的图形.

注意： [1] fun必须是M文件的函数名或是独立变量为x的字符串.

[2] fplot函数不能画参数方程和隐函数图形，但在一个图上可以画多个图形.

例在[-1，2]上画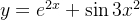 $y=e^{2x}+\sin 3x^{2}$ 的图形.

function Y=myfun1(x)
Y=exp(2*x)+sin(3*x.^2)
fplot(‘myfun1’,[-1,2])

例在[-2,2]范围内绘制函数tanh的图形.

fplot(‘tanh’,[-2,2])

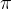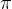例 x、y的取值范围都在[-2 $\pi$ ，2 $\pi$ ]，画函数tanh(x),sin(x),cos(x)的图形.

fplot(‘[tanh(x),sin(x),cos(x)]’,2*pi*[-1 1 –1 1])

3. 对数坐标图

在很多工程问题中,通过对数据进行对数转换可以更清晰地看出数据的某些特征,在对数坐标系中描绘数据点的曲线,可以直接地表现对数转换.对数转换有双对数坐标转换和单轴对数坐标转换两种.用loglog函数可以实现双对数坐标转换,用semilogx和semilogy函数可以实现单轴对数坐标转换.

loglog(Y) 表示 x、y坐标都是对数坐标系

semilogx(Y) 表示 x坐标轴是对数坐标系

semilogy(…) 表示y坐标轴是对数坐标系

plotyy 有两个y坐标轴，一个在左边，一个在右边

例用方形标记创建一个简单的loglog.

x=logspace(-1,2);
loglog(x,exp(x),’-s’)
grid on     %标注格栅

例创建一个简单的半对数坐标图.

x=0:.1:10;
semilogy(x,10.^x)

3.三维图形

空间曲线

1. 一条曲线

plot3(x,y,z,s)

x,y,z: n维向量，分别表示曲线上点集的横坐标、纵坐标、函数值

s: 指定颜色、线形等

例在区间[0，10π]画出参数曲线 x=sint,y=cost,z=t.

t=0:pi/50:10*pi;
plot3(sin(t),cos(t),t)
rotate3d  %旋转

2. 多条曲线

plot3(x,y,z)

其中x，y，z是都是m×n矩阵，其对应的每一列表示一条曲线.

例画多条曲线观察函数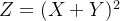 $Z=(X+Y)^{2}$ .

x=-3:0.1:3;y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
plot3(X,Y,Z)

（这里meshgrid(x,y)的作用是产生一个以向量x为行、向量y为列的矩阵）

空间曲面

(1) surf(x,y,z) 画出数据点（x，y，z）表示的曲面

x,y,z: 数据矩阵.分别表示数据点的横坐标、纵坐标、函数值

例画函数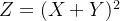 $Z=(X+Y)^{2}$ 的图形.

x=-3:0.1:3;
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
surf(X,Y,Z)
shading  flat    %将当前图形变得平滑

（2）mesh(x,y,z) 画网格曲面

画出曲面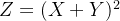 $Z=(X+Y)^{2}$ 在不同视角的网格图.

x=-3:0.1:3;   
y=1:0.1:5;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
mesh(X,Y,Z)

(3)meshz(X,Y,Z) 在网格周围画一个curtain图(如,参考平面)

处理图形

1. 在图形上加格栅、图例和标注

（1）GRID ON: 加格栅在当前图上

GRID OFF: 删除格栅

（2）hh = xlabel(string): 在当前图形的x轴上加图例string

hh = ylabel(string): 在当前图形的y轴上加图例string

hh = zlabel(string): 在当前图形的z轴上加图例string

hh = title(string): 在当前图形的顶端上加图例string

例在区间[0,2π]画sin(x)的图形，并加注图例“自变量X”、“函数Y”、“示意图”, 并加格栅.

x=linspace(0,2*pi,30);
y=sin(x);
plot(x,y)
xlabel('自变量X')
ylabel('函数Y')
title('示意图')
grid on

（3） hh = gtext(‘string’)

命令gtext(‘string’)用鼠标放置标注在现有的图上. 运行命令gtext(‘string’)时，屏幕上出现当前图形，在图形上出现一个交叉的十字，该十字随鼠标的移动移动，当按下鼠标左键时，该标注string放在当前十交叉的位置.

例在区间[0,2π]画sin(x)，并分别标注“sin(x)” ”cos(x)”.

x=linspace(0,2*pi,30);
y=sin(x);
z=cos(x);
plot(x,y,x,z)
gtext(‘sin(x)’);gtext(’cos(x)’)

2. 定制坐标

Axis([xmin xmax ymin ymax zmin zmax]) 定制图形坐标

例在区间[0.005,0.01]显示sin(1/x)的图形.

x=linspace(0.0001,0.01,1000);
y=sin(1./x);
plot(x,y)
axis([0.005 0.01 –1 1])

3. 图形保持

(1) hold on 保持当前图形, 以便继续画图到当前图上

hold of 释放当前图形窗口

例将y=sin(x)、y=cos(x)分别用点和线画出在同一屏幕上.

x=linspace(0,2*pi,30);
y=sin(x);
z=cos(x)
plot(x,z,:)
hold on
Plot(x,y)

(2) figure(h) 新建h窗口，激活图形使其可见，并把它置于其它图形之上

例区间[0,2 ]新建两个窗口分别画出y=sin(x)；z=cos(x).

x=linspace(0,2*pi,100);
y=sin(x);z=cos(x);
plot(x,y);
title('sin(x)');
pause
figure(2);
plot(x,z);
title('cos(x)');