LeetCode:162. 寻找峰值、1901. 寻找峰值 II(二分 C++)
目录
162. 寻找峰值
题目描述:
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [ 1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2; 或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
实现代码与解析:
二分
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int l = 0, r = nums.size() - 1;
while (l < r) {
int mid = (l + r) >> 1;
if (nums[mid] < nums[mid + 1]) l = mid + 1;
else r = mid;
}
return l;
}
};原理思路:
二分,如果mid值比右侧小,说明峰值在右侧,若大于等于,所以峰值为本身或其左侧。
1901. 寻找峰值 II
题目描述:
一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。
给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。
你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。
要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法
示例 1:
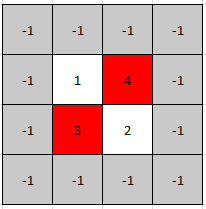
输入: mat = [[1,4],[3,2]] 输出: [0,1] 解释: 3 和 4 都是峰值,所以[1,0]和[0,1]都是可接受的答案。
示例 2:
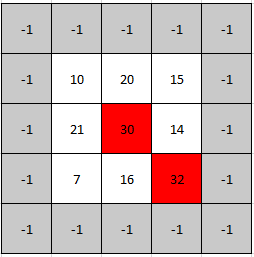
输入: mat = [[10,20,15],[21,30,14],[7,16,32]] 输出: [1,1] 解释: 30 和 32 都是峰值,所以[1,1]和[2,2]都是可接受的答案。
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105- 任意两个相邻元素均不相等.
实现代码与解析:
二分
class Solution {
public:
// 求一行中的最大值
int idx_max(vector<int>& m) {
return max_element(m.begin(), m.end()) - m.begin();
}
vector<int> findPeakGrid(vector<vector<int>>& mat) {
int l = 0, r = mat.size() - 1;
while (l < r) {
int mid = (l + r) >> 1;
int k = idx_max(mat[mid]);
if (mat[mid][k] > mat[mid + 1][k]) r = mid;
else l = mid + 1;
}
return {l, idx_max(mat[l])}; // 返回找到的行的最大值
}
};原理思路:
还是二分,把二维压缩到一维,取每一行的最大值作为其代表,因为每一行的最大值一定比左右值大,只需要再从每一行的最大值中上下对比像第一题一样二分即可。
为什么这样可以?因为此行的最大值要是小于其上或下对应行位置的值,那么其上或下行上的最大值肯定比此行所有的数要大,这样就不会越过此mid界限,从而达到了二分的效果。