graphlib中文API文档
graphlib中文API文档
(一)API 参考
该页面介绍graphlib中主要的概念及有关API。默认,有关功能和对象都在graphlib命名空间下。
文章目录
- graphlib中文API文档
- (一)API 参考
- (1)图概念
- (2)基础 API
- (3)算法 API
- 01) alg.components(graph)
- 02) alg.dijkstra(graph, source, weightFn, edgeFn)
- 03) alg.dijkstraAll(graph, weightFn, edgeFn)
- 04) alg.findCycles(graph)
- 05) alg.floydWarshall(graph, weightFn, edgeFn)
- 06) alg.isAcyclic(graph)
- 07) alg.postorder(graph, vs)
- 08) alg.preorder(graph, vs)
- 09) alg.prim(graph, weightFn)
- 10) alg.tarjan(graph)
- 11) alg.topsort(graph)
(1)图概念
graphlib仅有一个图的概念: Graph。创建新的实例可以使用下面的代码:
var g = new Graph()
默认, 会创建一个有向图且不支持节点间具有多条边或者由多个节点构成的复合节点。添加如下参数可以在构建具有特定性质的新的图对象:
- directed: 该参数设定为
true会获得有向图实例,设定为false会获得无向图实例。无向图不关心在边中节点相互关联的次序。换一种方式来说,g.edge("a", "b") === g.edge("b", "a")对无向图而言是成立的。该属性默认为:true。 - multigraph: 设定为
true允许图在同一对节点之间具有多条边。该属性默认为:false。 - compound: 设定为
true允许图具有复合节点,也就是说允许某结点是一些其他节点的父节点。该属性默认为:false。
要设定这些属性, 可以通过带有参数的Graph构造函数来创建对象。例如, 要创建一个有环且具有复合节点, 且一对节点之间允许具有多条边的图,可以通过下面的代码实现:
var g = new Graph({directed: true, compund: true, multigraph: true})
1)节点和边的表示
在graphlib中, 节点可以通过用户定义的字符串作为id来表述。所有节点有关的方法均使用此String类型的id来唯一标识此节点。下面代码可以实现关于节点的交互操作:
var g = new Graph()
g.setNode("my-id", "my-label");
g.node("my-id"); // 返回 "my-label"
graphlib中的边可以通过节点的连接关系来标识, 例如:
var g = new Graph();
g.setEdge("source", "target", "my-label");
g.edge("source", "target"); // 返回 "my-label"
然而, 对于各种对边的查询(例如: outEdges等)需要能够唯一标识一条边。通过使用edgeObj来实现。这个对象是由如下属性构成:
- v: 边的源头
source或尾部tail节点对象的id - w: 边的目标
target或头部head节点对象的id - name(可选): 该名称可以唯一标识一对节点中多条边的一个
任何边有关的函数来获得边的id都会通过edgeObj。例如:
var g = new Graph()
g.setEdge("source", "target", "my-label");
g.edge({v: "source", w: "target"}); // 返回 "my-label"
2)多边图(Multigraphs)
能够在一对节点之间包含多条边的图称作多边图multigraph。默认graphlib创建的图不支持节点间多边, 但通过在构造函数中设定参数multigraph属性为true可以构建这种图:
var g = new Graph({multigraph: true})
由于在一对节点中会出现多条边, 就需要一种方式来标识其中的任意一条。通过使用name属性来标识一对节点之间多条边中的一条:
var g = new Graph({multigraph: true})
g.setEdge("a", "b", "edge1-label", "edge1");
g.setEdge("a", "b", "edge2-label", "edge2");
g.edge("a", "b", "edge1"); // 返回 "edge1-label"
g.edge("a", "b", "edge2"); // 返回 "edge2-label"
g.edges(); // 返回 [{v: "a", w: "b", name: "edge1"}, {v: "a", w: "b", name: "edge2"}]
多变图允许不具有名字的边被创建:
var g = new Graph({ multigraph: true });
g.setEdge("a", "b", "my-label");
g.edge({v: "a", w: "b"}); // 返回 "my-label"
3)复合节点图(Compound Graphs)
节点可以是其他节点的父节点的图称作复合节点图。所有的子节点来自一个子图subgraph。通过如下代码能够创建一个复合节点图:
var g = new Graph({compound: true})
g.setParent("a", "parent");
g.setParent("b", "parent");
g.parent("a") // 返回 "parent"
g.parent("b") // 返回 "parent"
g.parent("parent"); // 返回 undefined
4)默认标签(Default Labels)
当节点和边被创建但未设定标签Label, 会被赋予默认的标签。参考setDefaultNodeLabel和setDefaultEdgeLabel。
(2)基础 API
(3)算法 API
01) alg.components(graph)
查询图中所有连接的节点组并返回这些节点组的数组。每个节点组都是一个数组包含了所有构成它的节点id。
该函数需要遍历约O(|V|)次。
例如:
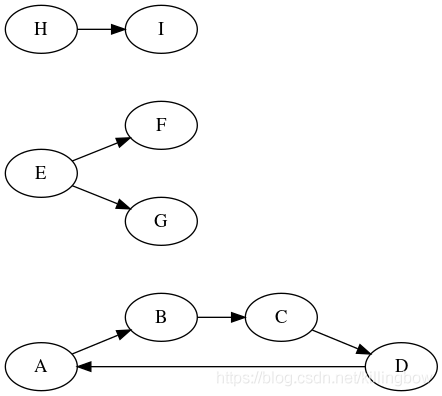
graphlib.alg.components(g);
// => [
// ['A', 'B', 'C', 'D'],
// ['E', 'F', 'G' ],
// ['H', 'I'],
// ]
02) alg.dijkstra(graph, source, weightFn, edgeFn)
该函数实现了Dijkstra算法, 会查询图g中从source节点到所有其它节点的最短路径。该函数会返回一个形式如v -> {distance, predecessor}的map。其中distance距离属性会获得source到v的最短路径上的权重合,如果没有任何路径可达则为Number.POSITIVE_INFINITY。另外的predecessor属性可以用来逆序遍历该source到v最短路径上的每个节点。
可选参数weightFn(e)为权重计算函数, 返回边e的权重。如果没有提供weightFn,那么每条边会被赋予权重1。当遍历的任何边的权重为负数时,该函数会抛出一个Error异常。
可选参数edgeFn(v)会在遍历事件中返回最短路径上所有边上节点的id。默认该函数会使用g.outEdges来获得该节点。
示例:
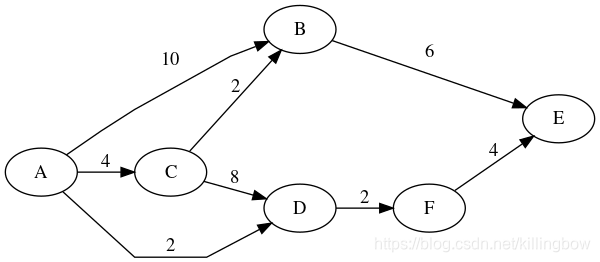
function weight(e) {return g.edge(e);}
graphlib.alg.dijkstra(g, "A", weight);
// => {
// A: {distance: 0},
// B: {distance: 6, predecessor: 'C'},
// C: {distance: 4, predecessor: 'A'},
// D:{distance: 2, predecessor: 'A'},
// E: {distance: 8, predecessor: 'F'},
// F: {distance: 4, predecessor: 'D'}
// }
03) alg.dijkstraAll(graph, weightFn, edgeFn)
该函数找到每个节点到所有其它可达节点的最短路径。它与alg.dijkstra相似,区别在于返回单源头数据single-source array, 它返回型如source -> alg.dijksta(g, source, weightFn, edgeFn)的map结构。
该函数的可选参数weightFn(e)是权重获得函数,返回边e的权重。如果没有提供weightFn所有的边会被假定具有相同的权重1。当遍历的边中包含负数权重,该函数会抛出Error异常。
该函数的可选参数edgeFn(u)返回到u节点时该最短路径中所有节点id。默认通过函数g.outEdges从边获得节点。
该函数需要遍历约O(|V| * ( |E| + |V| ) * log |V|)次。
示例:
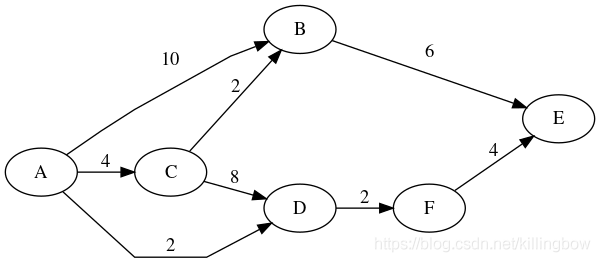
function weight(e) { return g.edge(e); }
graphlib.alg.dijkstraAll(g, function(e) { return g.edge(e); });
// => { A:
// { A: { distance: 0 },
// B: { distance: 6, predecessor: 'C' },
// C: { distance: 4, predecessor: 'A' },
// D: { distance: 2, predecessor: 'A' },
// E: { distance: 8, predecessor: 'F' },
// F: { distance: 4, predecessor: 'D' } },
// B:
// { A: { distance: Infinity },
// B: { distance: 0 },
// C: { distance: Infinity },
// D: { distance: Infinity },
// E: { distance: 6, predecessor: 'B' },
// F: { distance: Infinity } },
// C: { ... },
// D: { ... },
// E: { ... },
// F: { ... } }
04) alg.findCycles(graph)
该函数对于图g返回存在于环上的所有节点。如果不止一个环存在于图中,该函数会以数组形式返回所有的环,每个环由其上所有节点的id数组表示。如果仅仅需要判定图中是否有环,方法alg.isAcyclic是更加有效的。
var g = new graphlib.Graph();
g.setNode(1);
g.setNode(2);
g.setNode(3);
g.setEdge(1, 2);
g.setEdge(2, 3);
graphlib.alg.findCycles(g);
// => []
g.setEdge(3, 1);
graphlib.alg.findCycles(g);
// => [ [ '3', '2', '1' ] ]
g.setNode(4);
g.setNode(5);
g.setEdge(4, 5);
g.setEdge(5, 4);
graphlib.alg.findCycles(g);
// => [ [ '3', '2', '1' ], [ '5', '4' ] ]
05) alg.floydWarshall(graph, weightFn, edgeFn)
该函数实现了弗洛伊德Floyd-Warshall算法,能够查询图中每个节点到其余所有节点的最短路径。类似于alg.dijkstraAll,区别在于弗洛伊德算法对于某些图会更加有效,且该函数也能够适应负数的权重。该函数返回型如source -> {target -> {distance, predecessor}的map。distance属性是source到target节点的权重合,如果没有可达路径则为Number.POSITIVE_INFINITY。predecessor属性可以用来逆序遍历从source到target最短路径上的所有元素。
该函数的可选参数weightFn(e)用于返回边e的权重。如果未提供weightFunc每个边的权重会被假设为1。
该函数的可选参数edgeFn(v)用于返回所有到v节点的最短路径上的节点id。默认该函数通过outEdges函数来获得图上节点的id。
该算法需要运行约 O(|V|^3)次。
示例:
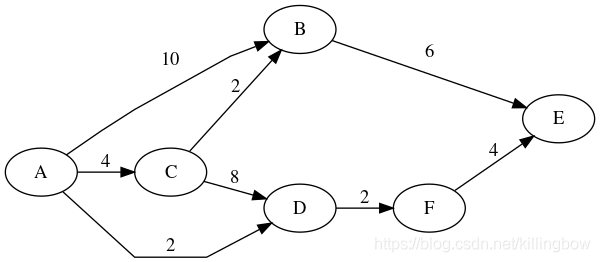
function weight(e) { return g.edge(e); }
graphlib.alg.floydWarshall(g, function(e) { return g.edge(e); });
// => { A:
// { A: { distance: 0 },
// B: { distance: 6, predecessor: 'C' },
// C: { distance: 4, predecessor: 'A' },
// D: { distance: 2, predecessor: 'A' },
// E: { distance: 8, predecessor: 'F' },
// F: { distance: 4, predecessor: 'D' } },
// B:
// { A: { distance: Infinity },
// B: { distance: 0 },
// C: { distance: Infinity },
// D: { distance: Infinity },
// E: { distance: 6, predecessor: 'B' },
// F: { distance: Infinity } },
// C: { ... },
// D: { ... },
// E: { ... },
// F: { ... } }
06) alg.isAcyclic(graph)
对于给定的图g,如果图内没有环则返回true否则返回false。该算法会在其探知到环时尽快返回。可以通过使用alg.findCycles函数来获得图内详细的环信息列表。
var g = new graphlib.Graph();
g.setNode(1);
g.setNode(2);
g.setNode(3);
g.setEdge(1, 2);
g.setEdge(2, 3);
graphlib.alg.isAcyclic(g);
// =>true
g.setEdge(3, 1);
graphlib.alg.isAcyclic(g);
// => false
07) alg.postorder(graph, vs)
该函数调用会对于图g以节点vs为起点,进行一次后序遍历postorder traversal。遍历过程中通过回调函数callback(v)来访问每个经过的节点v。
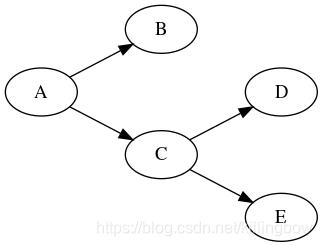
graphlib.alg.postorder(g, "A");
// => One of:
// [ "B", "D", "E", C", "A" ]
// [ "B", "E", "D", C", "A" ]
// [ "D", "E", "C", B", "A" ]
// [ "E", "D", "C", B", "A" ]
08) alg.preorder(graph, vs)
该函数调用会对于图g以节点vs为起点,进行一次前序遍历。遍历过程中通过回调函数callback(v)来访问每个经过的节点v。
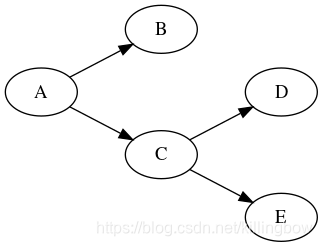
graphlib.alg.preorder(g, "A");
// => One of:
// [ "A", "B", "C", "D", "E" ]
// [ "A", "B", "C", "E", "D" ]
// [ "A", "C", "D", "E", "B" ]
// [ "A", "C", "E", "D", "B" ]
09) alg.prim(graph, weightFn)
对于连通的无向图通过Prim算法能够获得最小生成树。该函数返回最小生成树作为无向图。该算法在算法导论第三版634页被提及。
该函数使用weightFn(e)来获得边e的权重。如果该图不是连通图,就会抛出错误Error。
该函数运行约O(|E| log |V|)次。
示例:
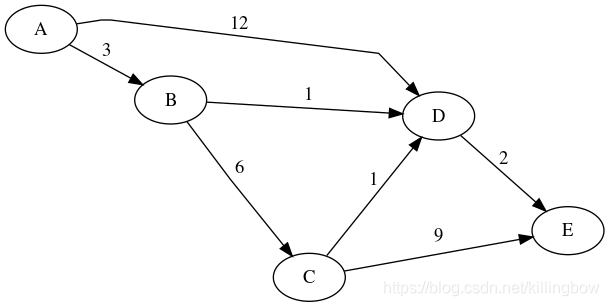
function weight(e) {return g(e);}
graphlib.alg.prim(g, weight);
将返回树(描述为图):
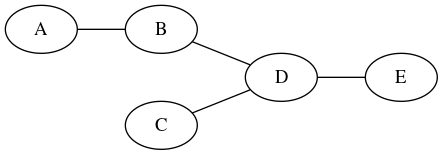
10) alg.tarjan(graph)
该函数实现了Tarjan算法,能够找到图g中的强连通部分。每一个强连通部分都是一组节点的集合,这些节点能够通过有向边到达该集合中的每个节点。强连通部分可以收缩为一个节点,该节点不再能与图中任何其它点到达或者反向到达。这样的强连通部分必然至少包含一个环。
示例:

graphlib.alg.tarjan(g);
// => [ [ 'F', 'G' ],
// [ 'H', 'D', 'C' ],
// [ 'E', 'B', 'A' ] ]
11) alg.topsort(graph)
topological sorting拓扑排序的一个实现。
对于图g该函数返回型如u -> v的边的数组,该数组中u先于v出现。如果该图中有环就无法生成这样的列表并且会抛出CycleException异常。
示例:
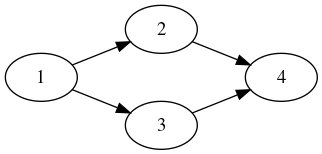
graphlib.alg.topsort(g)
// [ '1', '2', '3', '4' ] or [ '1', '3', '2', '4' ]