编译原理第二章课后习题，文法的二义性判断、语法树以及最左最右推导

第二章

1、文法G=（{A，B，S}，{a,b,c}P,S)，其中P为S→Ac|aB，A→ab，B→bc

写出L(G[S])的全部元素。

答：L(G[S])={abc}

2、文法G[N]为N→D|ND、D→0|2|3|4|5|6|7|8|9|，G[N]的语言是什么？

 答：允许零开头的所有非负整数

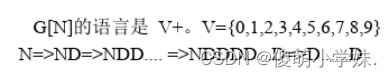
3、为只包含数字、加号和减号的表达式，例如9-2+5、3-1、7等构造一个文法。

 

5、已知文法G[Z]为Z→aZb|ab,写出L（G[Z]）的全部元素。

答：Z =>aZb =>aaZbb =>aaa..Z..bbb =>aaa..ab..bbb

L（G[Z]）={ab|n>=1}

6、已知文法G：

<表达式>::= <项>|<表达式>+<项>

<项>::= <因子>|<项>*<因子>

<因子>::=(<表达式>)|i

是给出下属表达式的推导以及语法树

（1）i 

 

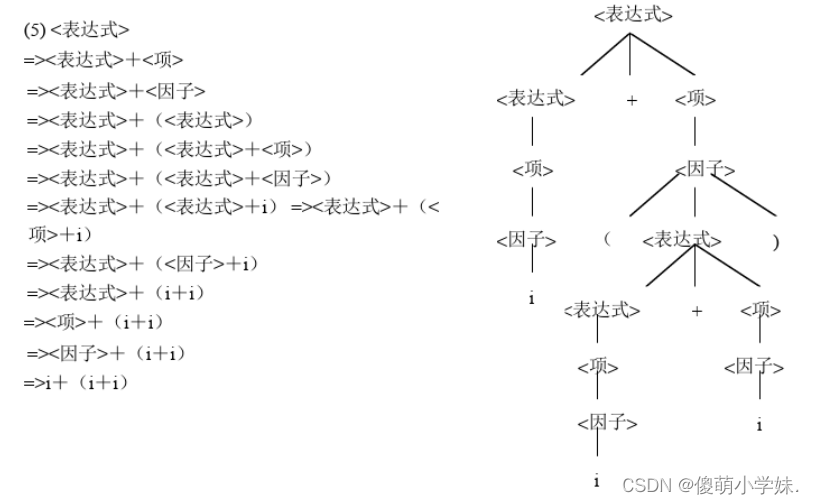
 （5）i+(i+i)

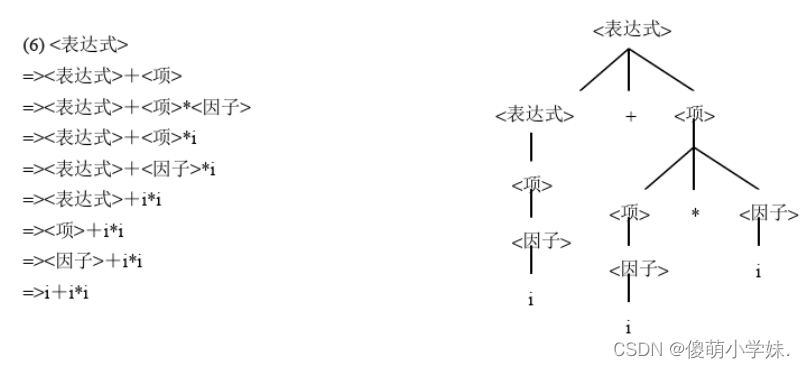
(6)i+i*i

 

 7、习题1中的文法是二义的吗？为什么？

文法G=（{A，B，S}，{a,b,c}P,S)，其中P为S→Ac|aB，A→ab，B→bc

答：最右推导：S=>Ac =>abc

                         S=>aB =>abc，

即存在两个不同的最右推导，所以该文法是二义的。

或者：

对输入字符串abc，能够造出如下两颗不同的语法树，所以该文法是二义的。

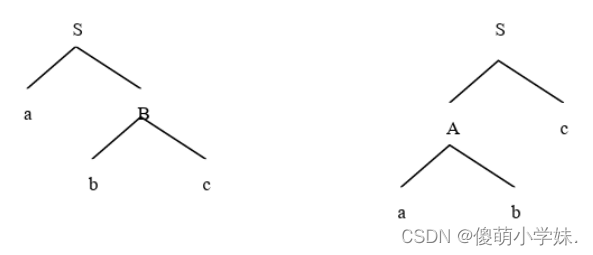
⭐⭐⭐那么问题来啦，怎么判断文法是不是具有二义性捏？

其实很简单，就看这个文法的某个句子如果有两个不同的最右（最左）推导，那这个文法就有二义性。

⭐⭐⭐又或者说可以用如下方法判断非二义性，

1.求出文法所有非终结符号的First集，

2.求出文法所有非终结符号的Follow集，

3.进行两步判断：

（1）非终结符号A的任何两个候选式的first集合不相交

（2）f若A的某个候选式可以推导出ε，则其它候选式的First集与Follow(A)不相交。

满足以上两个条件的文法一定是非二义性的。

10、令文法G[E]为

        E=>T|E+T|E-T

        T=>F|T*F|T/F

        F=>(E)|i

证明E+T*F是它的一个右句型，并指出这个句型的所有的短语，直接短语和句柄。

答：此句型对应的语法树如下，

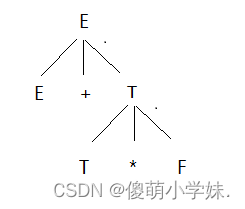
短语：E+T*F、T*F   

 直接短语：T*F   

句柄：T*F

 ⭐⭐⭐那么问题又来了！！怎么找出短语，直接短语和句柄捏？

短语：一个句型的语法树中任一子树叶结点所组成的符号串都是该句型的短语。

直接短语：如果子树中不再包含其他的子树，即A只能推导出b，而b不能再推出其他的式子，则b为此句型的直接短语。

句柄：直接短语中的最左直接短语为该句型的句柄。

11、一个上下文无关文法生成句子abbaa的唯一语法树如下：

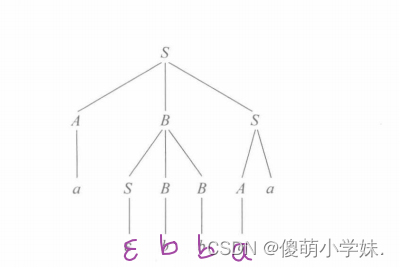
 （1）给出该句子相应的最左推导和最右推导。

        最左：S=>ABS=>aBS=>aSBBS=>aBBS=>abBS=>abbS=>abbAa=>abbaa

        最右：S=>ABS=>ABAa=>ABaa=>ASBBaa=>ASBbaa=>ASbbaa=>Abbaa=>abbaa

(3)找出该句子的所有短语，简单短语，句柄。

短语：a是相对于A的短语，ε 是S的短语，b是B的短语，ε bb是相对于B的短语，aa是S的短语，

aεbbaa是S的短语。

直接短语：a,ε ,b

句柄：a