基于卷积神经网络的高光谱分类 CNN+高光谱+印度松数据集
基于卷积神经网络的高光谱分类
一、研究现状
只考虑到高光谱图像的光谱特征,即:
1、提取特征(小波变换、Gabor纹理分析、形态学剖面)
2、利用分类方法分类(支持向量机、决策树、随机森林、神经网络)
缺点:这些特征提取方法需要依据先验知识手动设置,且通过设定参数提取的特征信息通常只能
用于区分特定的对象,缺乏灵活性,并且分类性能无法进一步提升。
本文提出:卷积神经网络的高光谱分类
优点:能同时提取图像中的1)光谱信息;2)空间信息;3)能够自动的学习和优化网络中的参数,
而不需要过多的人工调整
二、高光谱图像
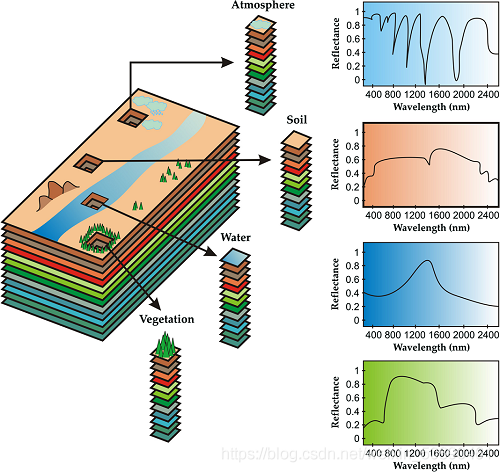
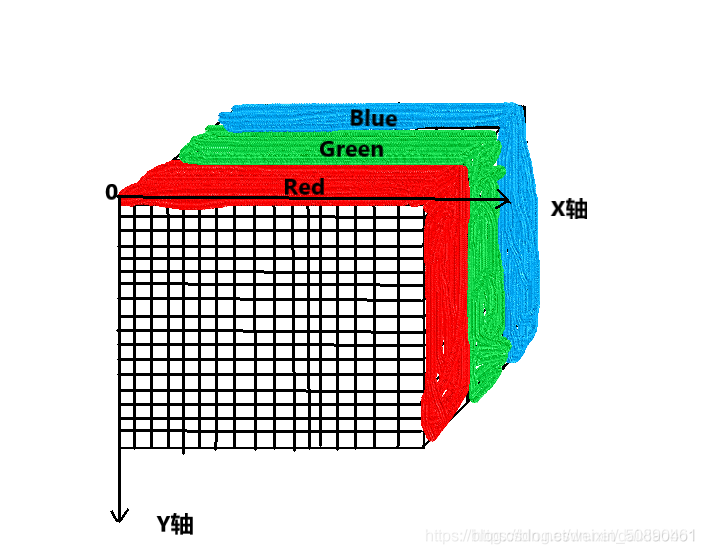
高光谱与RGB三通道图像的最大不同是,其具有上百个通道(就是一个三维的数据立方体)假如一个N X N X B 的图像,RGB图像的B维度有三个通道,高光谱图像的B维度有上百个通道(他的光谱维度)
高光谱的三维:二维几何空间及一维光谱信息
光谱维度展开不仅可以获得图像上每个点的光谱数据,还可以获得任一个谱段的影像信息
三、降维
PCA(主成分分析)
主成分分析(Principal Component Analysis,简称为 PCA)PCA 变换又称为霍特林变换(hotelling transform)和K-L (karhunen-loeve)变换。
是一种用于多变量数据信息提取的降维算法(提取数据的主要特征分量),离散 K-L 变换是理论基础,PCA 也被称为特征脸方法。其主要思想是通过计算不同维度图像训练样本与各维训练样本均值的差值之间的相关性,评估各维空间特征表征整体空间特征的能力,再将所有图像样本最大特征值对应的特征向量投影到较低维度空间,最终实现降维。
算法具体描述如下:
1、 数据预处理。假设有 M 维图像数据,I1, I2, … … I𝑀,作为训练样本,每个图像由 m 行和 n 列像素组成。假设多维信息各维度数据不相关,将所有图像转换为图像向量Γ1, Γ2, … … Γ𝑀,并且每个图像向量的维度为m × n。
2、计算特征空间。
3、 投影与相似性检验。
四、CNN
组成:一般包括全连接层、卷积层、<激活函数层>、池化层(有平均池化、最大池化两种)有了这些层使得卷积神经网络有了可以拟合各种函数的能力。
作用:通过卷积运算,将图像进行降维,使其可以进行训练

卷积操作示意(通过3x3的卷积核进行特征提取)
1)卷积层

通过卷积核(kernel)和原始图像上等同大小的区域进行卷积运算,通过计算得到特征图(与图像等同大小的尺寸的像素点进行对应相乘,再将相乘结果相加得到特征图上的特征值)
卷积核的参数不同提取到的特征不同,一个卷积层可以有多个卷积核,低层的卷积层提取到的是边框、颜色等简单特征;中层提取到低层特征的集合;高层提取到图像的全局特征
2)池化层(最大池化Max-Pooling)
池化有:最大池化,均值池化
经卷积后,特征表达空间较大,存在较多冗余信息(特征)
池化操作:缩小参数矩阵(去除冗余信息);从而减小下一层参数的数量;(防止过拟合,减小计算量)
-
保留特征图中最重要的特征并去除无关的特征。
-
减小特征图 (Feature Map) 的维数,从而减小后续的计算量。
-
减少了模型需要训练的参数量,降低了模型的复杂度,使得模型更为简单些,起到了稀疏模型的作用,提高了模型的泛化能力。
-
引入了一定的不变性,包括平移不变性、旋转不变性以及尺度不变性。
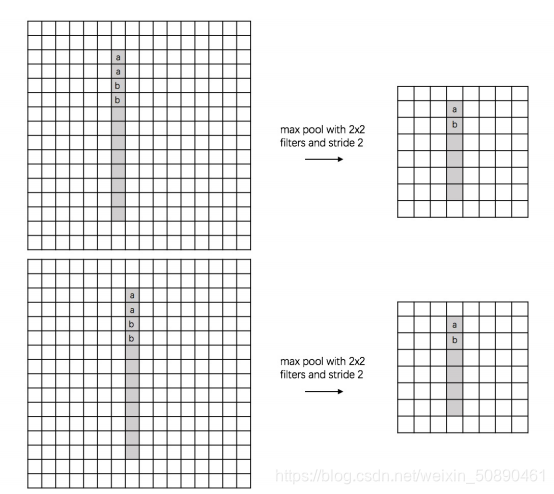
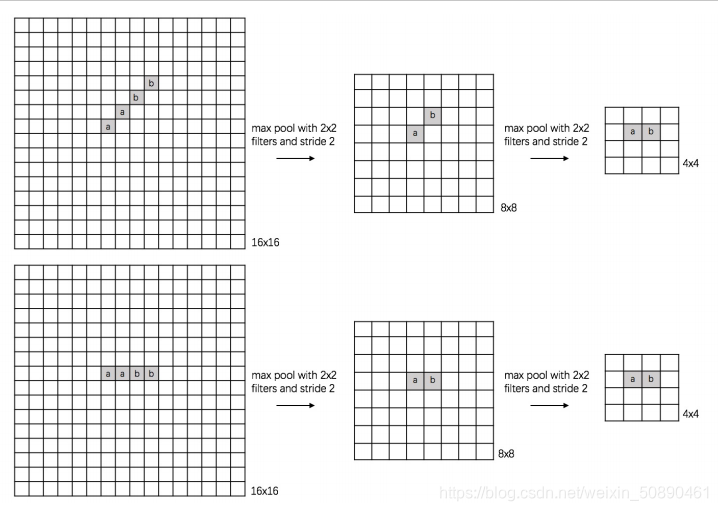
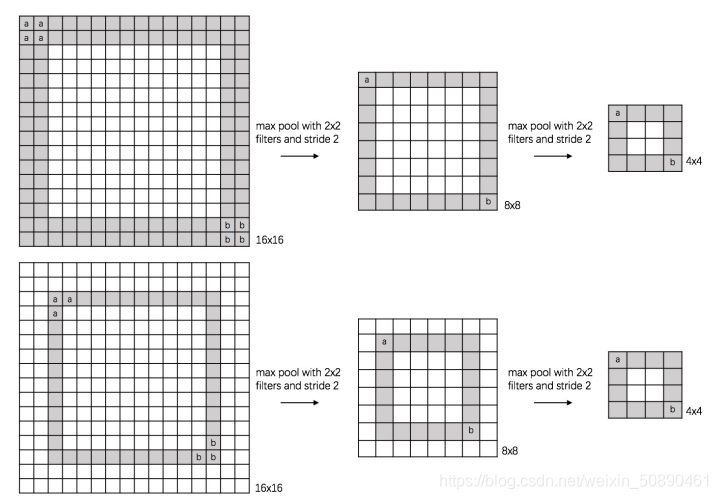
池化层是对小区域数据(局部区域)进行将维,因此可以同时在水平方向和数值上进行降维(减小特征图尺寸)
3)全连接层
在卷积神经网络中,卷积层和池化层等操作可以看做是将原始图片映射到一个低维的隐层特征空间,而全连接层则起到将学习到的分布式特征表示映射到样本标记空间的作用
4)激活函数层
1、sigmoid
2、tanh
3、ReLu
只保留响应值大于 0 的数值,并将小于等于 0 的响应值置为 0
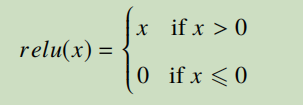
ReLU 函数的优点在于它会增加前一层网络乃至整个卷积神经网络的非线性特征,同时因为保留了响应为正的值,不会影响到卷积层提取出的特征,当输入比较大时不会存在梯度消失的情况,成功地解决了因梯度消失而造成的卷积神经网络学习收敛慢的问题。并且只需要一个阈值就可以得到神经网络的激活值,不需要复杂度运算,ReLU 主要用在神经网络中的隐藏层作为激活函数。另外数据通常有很多的冗余,而近似程度的最大化地保留数据特征,可以通过一个绝大多数值为 0 的稀疏矩阵来实现。对于 ReLU 而言,神经网络反复迭代训练的过程,实际上相当于在不断试探如何用一个稀疏矩阵表达图像特征,因为数据的稀疏特性的存在,所以这种方法可以在提高训练速度的同时又保证模型的效果。
4)dropout层
前向传播时,让某个神经元的激活值以一定概率停止工作(使模型泛化性增,因为这样让其不会对某一特征太过依赖)【针对数据不平衡】
5)Flatten层
Flatten层用来将输入“压平”,即把多维的输入一维化,常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小。
batch理解:
CNN train 的样张图片 60 张,设置 batch_size = 15;
理解:训练数据图片一次取15张同时训练,分4次训练完。
五、数据集
印度松
该场景由AVIRIS传感器收集在印第安纳州西北部的印第安松树测试点上,由145×145像素和224个光谱反射带组成,其波长范围为0.4–2.5 10 ^(-6)米。此场景是较大场景的子集。印度松树景观包含三分之二的农业,以及三分之一的森林或其他天然多年生植物。有两条主要的双车道高速公路,一条铁路线,以及一些低密度房屋,其他建筑物和较小的道路。由于场景是在6月拍摄的,因此目前的一些农作物(玉米,大豆)处于生长的初期,覆盖率不足5%。现有的地面真理被划分为十六个等级,并且并不都是相互排斥的。通过删除覆盖吸水区域的条带,我们也将条带的数量减少到200条:[104-108],[150-163],220。Pursue的大学MultiSpec网站。
下载MATLAB数据文件:印度松(6.0 MB) | 更正的印度松(5.7 MB) | 印度松树groundtruth(1.1 KB)

印度松树数据集的样本带
Indian Pines的Groundtruth数据集
| Indian Pines场景的Groundtruth类及其各自的样本数 | ||
|---|---|---|
| # | 类 | 样品 |
| 1 | 紫花苜蓿 | 46 |
| 2 | 玉米not | 1428 |
| 3 | 玉米薄荷 | 830 |
| 4 | 玉米 | 237 |
| 5 | 草场 | 483 |
| 6 | 草树 | 730 |
| 7 | 割草草 | 28 |
| 8 | 干草堆 | 478 |
| 9 | 燕麦 | 20 |
| 10 | 大豆芥末 | 972 |
| 11 | 大豆薄荷 | 2455 |
| 12 | 大豆清洁 | 593 |
| 13 | 小麦 | 205 |
| 14 | 树木 | 1265 |
| 15 | 建筑物-草木-树木驱动器 | 386 |
| 16 | 石钢塔 | 93 |
六、基于卷积神经网络的高光谱分类
1、分类算法
高光谱图像分类的不同算法
-
K-Nearest Neighbors
K最近邻居
-
Support Vector Machine
支持向量机
-
Spectral Angle Mapper
光谱角映射器
-
Convolutional Neural Networks
卷积神经网络
-
Decision Trees e.t.c
决策树等
针对给定输入数据预测类别标签
分类可分为:
-
Classification Predictive Modeling
分类预测建模
-
Binary Classification
二进制分类
-
Multi-Class Classification
多类别分类
-
Multi-Label Classification
多标签分类
-
Imbalanced Classification
分类不平衡
2、模型搭建
1)、输入(预处理图像)
(1)对高光谱图像进行空间取块
为了与深度卷积神经网络的输入相匹配
以空间上的一个像元为中心,取周围N X N大小的块 即每个小块大小为N X N X B ;B为图像的通道数
(2)降维
对于N X N X B的高光谱图像,由于其有数百维的光谱波段(观瀑维度 即:B),增加了网络训练的难度(计算成本高)
本文采用pca即主成分分析的方法进行降维
通过1) 2)操作不仅可以去除光谱中的冗余信息同时又保留了图像的空间信息
2)、模型结构
model = Sequential()
model.add(Conv2D(C1, (3, 3), activation='relu', input_shape=input_shape))
model.add(Conv2D(3*C1, (3, 3), activation='relu'))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(6*numPCAcomponents, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(16, activation='softmax'))

3、代码结构
dataset.py
利用spectral工具包读取数据集,然后对数据集进行预处理,包括进行训练测试集分割 / 序列化和PCA变换,并将其以npy的格式保存到文件中.处理后的数据集保存在predata文件夹中.
train.py
利用keras构建卷积神经网络模型,读取与处理的数据集进行训练.
其中训练过程,使用随机梯度下降法SGD作为优化算法,使用多分类的对数损失函数categorical_crossentropy作为损失函数.
使用ReduceLROnPlateau回调函数对val_acc(验证集准确率)进行监控,当val_acc不再下降时,减少学习率,直至减少到0.000001.
使用ModelCheckpoint回调函数,对有好的val_acc的训练过程作为一个检查点保存下来,下一次若有更好的结果则更新.若不好则不更新.
训练完成后保存模型到文件,并将训练过程中loss和accuarcy的变化情况绘制出来.
test.py
对训练的模型的效果进行测试和评价.
使用sklearn包中的classification_report和confusion_matrix,总结出分类效果报告(包括Test loss Test accuracy以及对测试集中每一类样本的预测结果进行统计)和相应的混淆矩阵.
使用matplotlib工具包将混淆矩阵可视化,包括原始的混淆矩阵(数据为样本个数)以及标准化后的混淆矩阵(数据为样本比例)
最后读取原始数据集,对整个数据集进行分类,并使用spectral工具包绘制出预测结果,以高光谱图像的形式表示出来.
4、训练结果
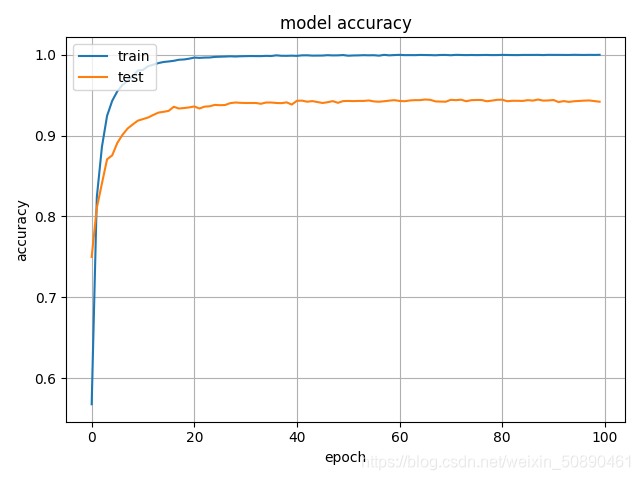
下图是训练和测试准确率随着epoch的变化图
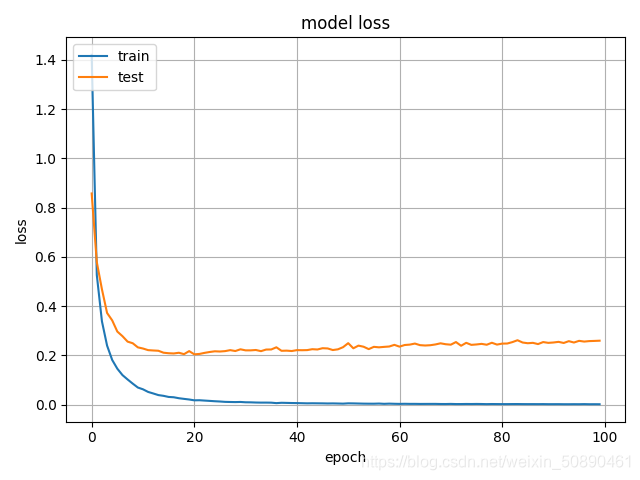
下图是训练和测试损失随着epoch的变化图
5、测试结果
Test loss 25.945746977841722 (%)
Test accuracy 94.18536585365854 (%)
classification result:
precision recall f1-score support
Alfalfa 1.00 0.91 0.95 23
Corn-notill 0.92 0.87 0.89 714
Corn-mintill 0.92 0.95 0.94 415
Corn 0.98 0.92 0.95 118
Grass-pasture 0.98 0.98 0.98 242
Grass-trees 0.99 0.99 0.99 365
Grass-pasture-mowed 1.00 1.00 1.00 14
Hay-windrowed 1.00 1.00 1.00 239
Oats 0.91 1.00 0.95 10
Soybean-notill 0.90 0.91 0.91 486
Soybean-mintill 0.92 0.95 0.94 1228
Soybean-clean 0.94 0.90 0.92 297
Wheat 1.00 1.00 1.00 102
Woods 0.98 0.98 0.98 633
Buildings-Grass-Trees-Drives 0.93 0.90 0.91 193
Stone-Steel-Towers 0.92 1.00 0.96 46
accuracy 0.94 5125
macro avg 0.96 0.95 0.95 5125
weighted avg 0.94 0.94 0.94 5125
使用classification_report函数得到:
(1)support列为每个标签出现的次数
(2)precision列精确度
(3)recall列召回率
(4)f1-score列为f1值即精确度和召回率的调和平均
(5)avg / total各列的均值 support列是总和
精确率:精确率越高,代表预测正确的标签的比例越高;【所有预测为这一类的标签中预测正确的标签所占的比例】
召回率:召回率越高,模型分类性能越好;【所有这一类标签中被正确分类出来的标签所占比例】
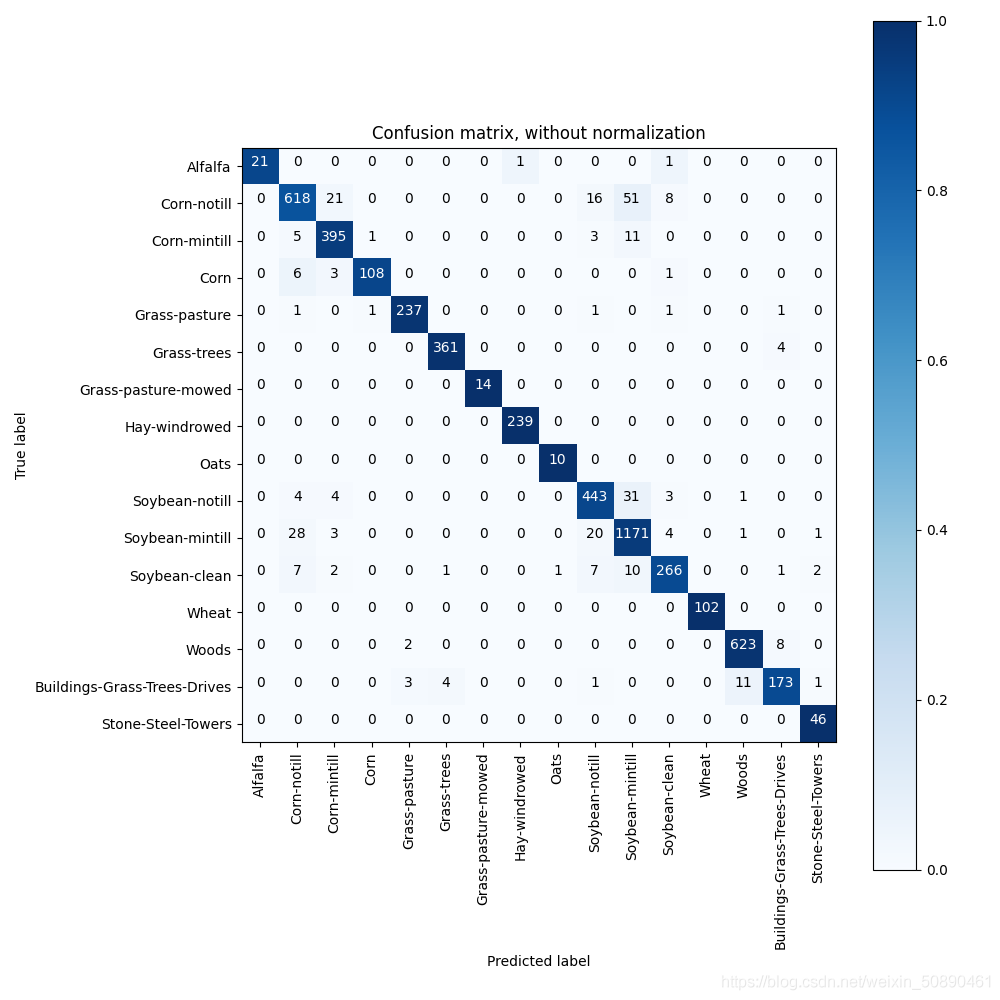
下图是没有经过标准化的混淆矩阵
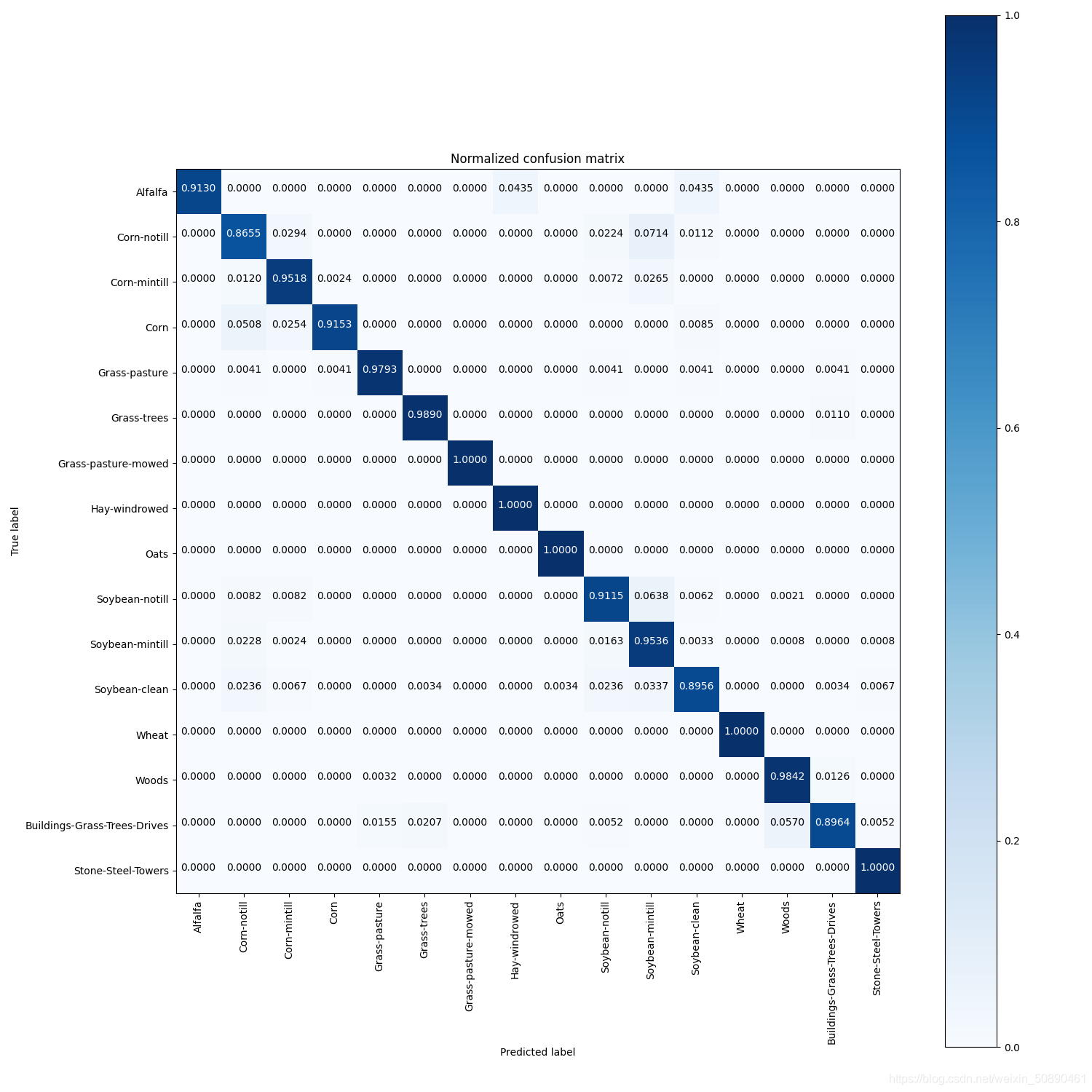
下图是经过标准化的混淆矩阵
下图是真实分类的高光谱图像
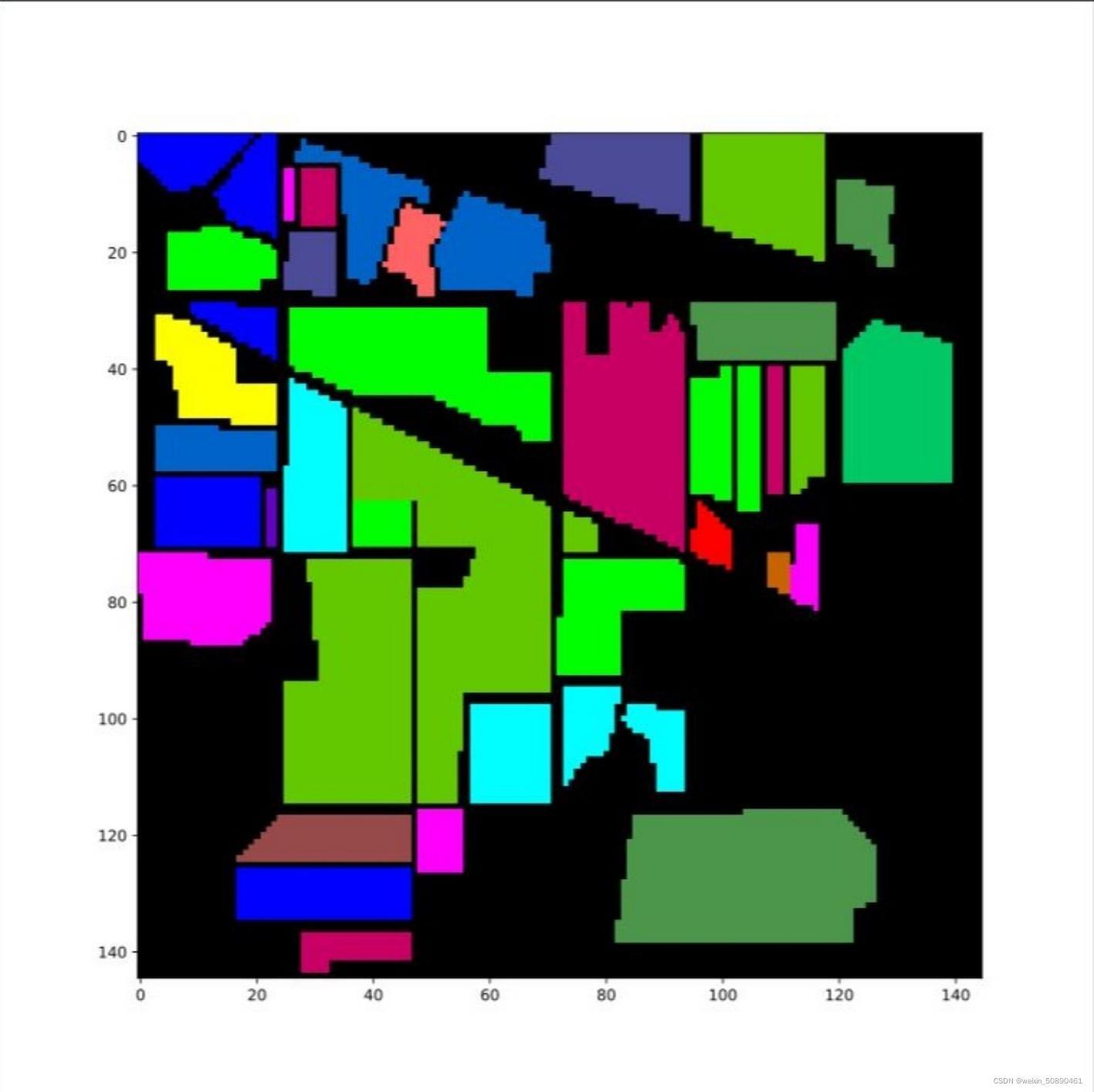
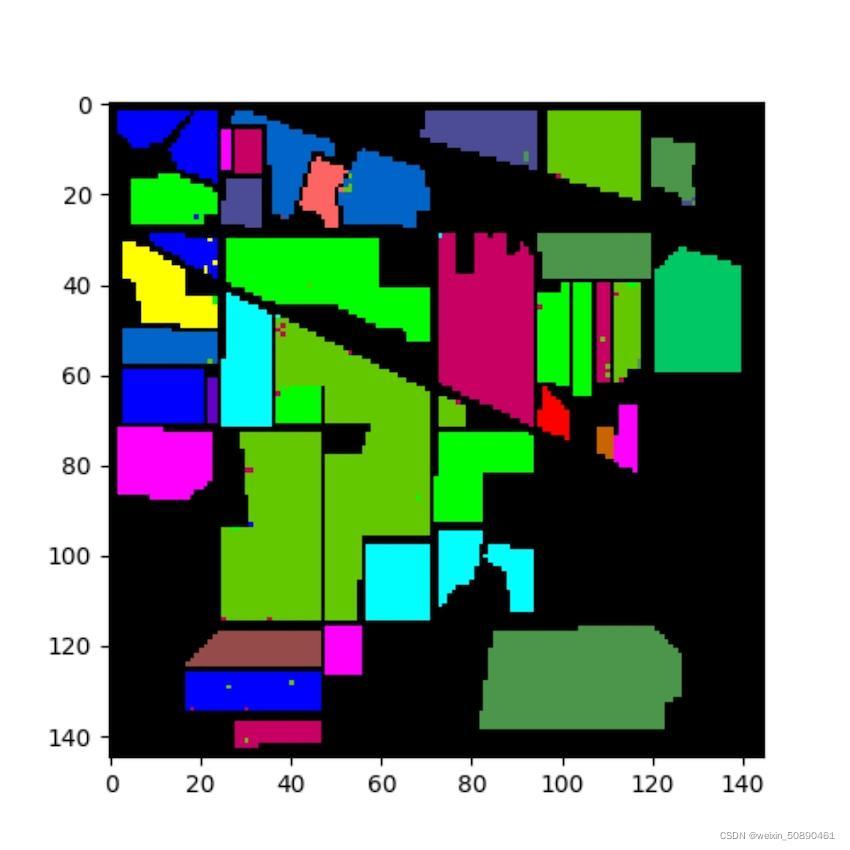
下图是经过上述模型分类的得到的高光谱图像
七、知识补充
1、随机梯度下降(stochastic gradient descent,SGD)
用于高维的优化
出处:https://www.zhihu.com/question/264189719/answer/291167114
- 随机梯度下降:在每次更新时用1个样本,可以看到多了随机两个字,随机也就是说我们用样本中的一个例子来近似我所有的样本,来调整θ,因而随机梯度下降是会带来一定的问题,因为计算得到的并不是准确的一个梯度,**对于最优化问题,凸问题,**虽然不是每次迭代得到的损失函数都向着全局最优方向, 但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近。但是相比于批量梯度,这样的方法更快,更快收敛,虽然不是全局最优,但很多时候是我们可以接受的。
2、混淆矩阵
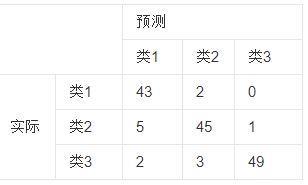
如有150个样本数据,预测为1,2,3类各为50个。分类结束后得到的混淆矩阵为:
每一行之和表示该类别的真实样本数量,每一列之和表示被预测为该类别的样本数量,
第一行说明有43个属于第一类的样本被正确预测为了第一类,有两个属于第一类的样本被错误预测为了第二类
3、欠采样 过采样
1:为什么类别不平横会影响模型的输出:
许多模型的输出类别是基于阈值的,例如逻辑回归中小于0.5的为反例,大于则为正例。在数据不平衡时**,默认的阈值会导致模型输出倾向与类别数据多的类别。**
因此可以在实际应用中,解决办法包括:
1)调整分类阈值,使得更倾向与类别少的数据。
2)选择合适的评估标准,比如ROC,AUC或者F1,G-mean,而不是准确度(accuracy)
3)过采样法(sampling):来处理不平横的问题。分为欠采样(undersampling)和过采样(oversampling)两种,
过采样:重复正比例数据,实际上没有为模型引入更多数据,过分强调正比例数据,会放大正比例噪音对模型的影响。
欠采样:丢弃大量数据,和过采样一样会存在过拟合的问题。
由于随机过采样采取简单复制样本的策略来增加少数类样本,这样容易产生模型过拟合的问题,即使得模型学习到的信息过于特别(Specific)而不够泛化(General)
小tip:过拟合:大家不必深究过拟合只要知道过拟合了,那么模型预测或者分类就和实际的情况相差甚远了,做机器学习的筒子,宁愿牺牲一些accuracy,也要抑制过拟合的情况产生,是一个令人很头疼的问题。
4)数据合成:SMOTE(Synthetic Minority Oversampling Technique)即合成少数类过采样技术,它是基于随机过采样算法的一种改进方案,SMOTE算法的基本思想是对少数类样本进行分析并根据少数类样本人工插值合成新样本()跟大类样本数据相当)添加到数据集中,构成均衡数据集。
4、训练集 验证集 测试集
训练集
验证集
1)确定超参数:在训练过程中,检验模型的状态、收敛情况。通常用来调整超参数,通过几组模型在验证集上的表现确定超参数;
2)判断何时停止训练:在训练过程中,监控模型是否发生过拟合。一般而言,验证集在表现稳定的情况下,若继续训练,训练集的表现还会继续上升,但是验证集会不升反降,这样一般就是发生了过拟合。因此,验证集通常被用作判断合适停止训练。
测试集
5、 回调函数
1)ReduceLROnPlateau回调函数
目的:定义学习率之后,经过一定epoch迭代之后,模型效果不再提升,该学习率可能已经不再适应该模型。需要在训练过程中缩小学习率,进而提升模型。如何在训练过程中缩小学习率呢?我们可以使用keras中的回调函数ReduceLROnPlateau。与EarlyStopping配合使用,会非常方便。
为什么初始化一个非常小的学习率呢?因为初始的学习率过小,会需要非常多次的迭代才能使模型达到最优状态,训练缓慢。如果训练过程中不断缩小学习率,可以快速又精确的获得最优模型。
monitor:监测的值,可以是accuracy,val_loss,val_accuracy
factor:缩放学习率的值,学习率将以lr = lr*factor的形式被减少
patience:当patience个epoch过去而模型性能不提升时,学习率减少的动作会被触发
mode:‘auto’,‘min’,‘max’之一 默认‘auto’就行
epsilon:阈值,用来确定是否进入检测值的“平原区”
cooldown:学习率减少后,会经过cooldown个epoch才重新进行正常操作
min_lr:学习率最小值,能缩小到的下限
Reduce=ReduceLROnPlateau(monitor='val_accuracy',
factor=0.1,
patience=2,
verbose=1,
mode='auto',
epsilon=0.0001,
cooldown=0,
min_lr=0)
2)ModelCheckpoint回调函数:在每个训练期之后保存模型
keras.callbacks.ModelCheckpoint(filepath, monitor='val_loss', verbose=0, save_best_only=False, save_weights_only=False, mode='auto', period=1)
filepath: 字符串,保存模型的路径。
monitor: 被监测的数据。
verbose: 详细信息模式,0 或者 1 。
save_best_only: 如果 save_best_only=True, 被监测数据的最佳模型就不会被覆盖。
mode: {auto, min, max} 的其中之一。 如果 save_best_only=True,那么是否覆盖保存文件的决定就取决于被监测数据的最大或者最小值。 对于 val_acc,模式就会是 max,而对于 val_loss,模式就需要是 min,等等。 在 auto 模式中,方向会自动从被监测的数据的名字中判断出来。
save_weights_only: 如果 True,那么只有模型的权重会被保存 (model.save_weights(filepath)), 否则的话,整个模型会被保存 (model.save(filepath))。
period: 每个检查点之间的间隔(训练轮数)
6、动量
Momentum(动量,冲量): 结合当前梯度与上一次更新信息,用于当前更新, 通常取值 momentum=0.9
7、学习率
学习率:用于控制更新的步长, 通常取值 lr=0.01
8、StratifiedShuffleSplit函数的使用
官方文档
用法:
from sklearn.model_selection import StratifiedShuffleSplit
StratifiedShuffleSplit(n_splits=10,test_size=None,train_size=None, random_state=None)12
2.1 参数说明
参数 n_splits是将训练数据分成train/test对的组数,可根据需要进行设置,默认为10
参数test_size和train_size是用来设置train/test对中train和test所占的比例。例如:
1.提供10个数据num进行训练和测试集划分
2.设置train_size=0.8 test_size=0.2
3.train_num=numtrain_size=8 test_num=numtest_size=2
4.即10个数据,进行划分以后8个是训练数据,2个是测试数据
注:train_num≥2,test_num≥2 ;test_size+train_size可以小于1
参数 random_state控制是将样本随机打乱
2.2 函数作用描述
1.其产生指定数量的独立的train/test数据集划分数据集划分成n组。
2.首先将样本随机打乱,然后根据设置参数划分出train/test对。
3.其创建的每一组划分将保证每组类比比例相同。即第一组训练数据类别比例为2:1,则后面每组类别都满足这个比例
2.3 具体实现
from sklearn.model_selection import StratifiedShuffleSplit
import numpy as np
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4],
[1, 2],[3, 4], [1, 2], [3, 4]])#训练数据集8*2
y = np.array([0, 0, 1, 1,0,0,1,1])#类别数据集8*1
ss=StratifiedShuffleSplit(n_splits=5,test_size=0.25,train_size=0.75,random_state=0)#分成5组,测试比例为0.25,训练比例是0.75
for train_index, test_index in ss.split(X, y):
print("TRAIN:", train_index, "TEST:", test_index)#获得索引值
X_train, X_test = X[train_index], X[test_index]#训练集对应的值
y_train, y_test = y[train_index], y[test_index]#类别集对应的值
12345678910111213
9、numpy.unique
numpy.unique(ar,return_index = False,return_inverse = False,return_counts = False,axis = None)
查找数组的唯一元素。
返回数组的排序后的唯一元素。除独特元素外,还有三个可选输出:
-
输入数组的索引给出唯一值
-
重建输入数组的唯一数组的索引
-
输入数组中每个唯一值出现的次数
-
参量
array_like输入数组。除非指定了轴,否则如果它不是一维的,它将被展平。return_index bool,可选如果为True,则还返回ar的索引(沿着指定的轴,如果提供的话,或者在展平的数组中),这将导致唯一的数组。return_inverse bool,可选如果为True,则还返回可用于重建ar的唯一数组的索引(对于指定的轴(如果提供))。return_counts bool,可选如果为True,则还返回每个唯一项出现在ar中的次数。1.9.0版中的新功能。轴int或无,可选要运行的轴。如果为None,则ar将被展平。如果为整数,则由给定轴索引的子数组将被展平并视为具有给定轴尺寸的一维数组的元素,有关更多详细信息,请参见注释。如果使用轴kwarg,则不支持对象数组或包含对象的结构化数组。默认为无。1.13.0版中的新功能。
-
退货
唯一ndarray排序后的唯一值。unique_indices ndarray,可选原始数组中唯一值的首次出现的索引。仅在return_index为True时提供。unique_inverse ndarray,可选从唯一数组重建原始数组的索引。仅在return_inverse为True时提供。unique_counts ndarray,可选每个唯一值出现在原始数组中的次数。仅在return_counts为True时提供。1.9.0版中的新功能。
也可以看看
-
numpy.lib.arraysetops
具有许多其他功能的模块,用于对阵列执行设置操作。
笔记
指定轴后,将对由该轴索引的子数组进行排序。通过将指定的轴设为数组的第一维(将轴移至第一维以保持其他轴的顺序),然后将子数组按C顺序展平,即可完成此操作。然后,将展平的子数组视为结构化类型,并为每个元素指定了标签,结果是我们最终得到了结构化类型的1-D数组,该数组可以用与其他任何1-D数组相同的方式处理。结果是,展平的子数组从第一个元素开始按字典顺序排序。
例子
>>>
>>> np.unique([1, 1, 2, 2, 3, 3])
array([1, 2, 3])
>>> a = np.array([[1, 1], [2, 3]])
>>> np.unique(a)
array([1, 2, 3])
返回二维数组的唯一行
>>>
>>> a = np.array([[1, 0, 0], [1, 0, 0], [2, 3, 4]])
>>> np.unique(a, axis=0)
array([[1, 0, 0], [2, 3, 4]])
返回给出唯一值的原始数组的索引:
>>>
>>> a = np.array(['a', 'b', 'b', 'c', 'a'])
>>> u, indices = np.unique(a, return_index=True)
>>> u
array(['a', 'b', 'c'], dtype='<U1')
>>> indices
array([0, 1, 3])
>>> a[indices]
array(['a', 'b', 'c'], dtype='<U1')
从唯一值重建输入数组:
>>>
>>> a = np.array([1, 2, 6, 4, 2, 3, 2])
>>> u, indices = np.unique(a, return_inverse=True)
>>> u
array([1, 2, 3, 4, 6])
>>> indices
array([0, 1, 4, 3, 1, 2, 1])
>>> u[indices]
array([1, 2, 6, 4, 2, 3, 2])
10、交叉熵损失函数
熵:
是"无序化"的度量
信息量
一件事发生的概率越小,信息量越大;
发生的概率越大,信息量越小。
举例理解:“国足踢进世界杯”信息量大 因为这件事发生的概率小;
“太阳从东方升起”信息量小 因为这件事大家习以为常,概率为一;
信息熵:
是“有序化”度量;
离散随机事件出现的概率
系统越是有序,信息熵越低;系统越是混乱,信息熵越高;
交叉熵原理:
交叉熵是用来衡量两个 概率分布 的距离(也可以叫差别)。[概率分布:即[0.1,0.5,0.2,0.1,0.1],每个类别的概率都在0~1,且加起来为1]。
若有两个概率分布p(x)和q(x),通过q来表示p的交叉熵为:(注意,p和q呼唤位置后,交叉熵是不同的)
只要把p作为正确结果(如[0,0,0,1,0,0]),把q作为预测结果(如[0.1,0.1,0.4,0.1,0.2,0.1]),就可以得到两个概率分布的交叉熵了,交叉熵值越低,表示两个概率分布越靠近。
交叉熵计算实例:
假设有一个三分类问题,某个样例的正确答案是(1,0,0),某个模型经过softmax回归之后的预测答案是(0.5,0.4,0.1),那么他们的交叉熵为:
如果另一个模型的预测概率分布为(0.8,0.1,0.1),则这个预测与真实的交叉熵为:
由于0.1小于0.3,所以第二个预测结果要由于第一个。
交叉熵使用背景:
通过神经网络解决分类问题时,一般会设置k个输出点,k代表类别的个数
每个输出结点,都会输出该结点对应类别的得分,如[cat,dog,car,pedestrian] 为[44,10,22,5]
但是输出结点输出的是得分,而不是概率分布,那么就没有办法用交叉熵来衡量预测结果和真确结果了,那怎么办呢,解决方法是在输出结果后接一层 softmax,softmax的作用就是把输出得分换算为概率分布。
11、高光谱降维方法
现有降维(Dimensionality Reduction, DR)方法总结
-
主成分分析(Principal Component Analysis, PCA)
-
线性判别分析(Linear Discriminant Analysis, LDA)维基
-
局部线性嵌入(Local Linear Embedding, LLE)
-
等距特征映射(ISOmetric feature MAPping, ISOMAP)
-
拉普拉斯本征映射(Laplacian Eigenmap, LE)
-
t-分布随机邻域嵌入(t-distribution Stochastic Neighbor Embedding, t-SNE)
-
局部保持投影(Locality Preserving Projections, LPP)
-
邻域保持嵌入(Neighborhood Preserving Embedding, NPE)
-
参数化监督t-SNE
-
图嵌入(Graph Embedding, GE)——尝试统一多种不同的降维方法
上述方法的问题是只考虑了光谱信息,没有考虑像元间的空间关联
-
空间相干NPE(Spatial Coherence NPE, SC-NPE)
-
局部像元NPE(Local Pixel NPE, LP-NPE)
-
判别空间-光谱边缘(Discriminate Spectral-Spatial Margins, DSSM) 链接
上述方法或是只利用空间信息来表征相似度,或是在一个特定的空间窗口中考虑空间关系,而没有从邻接图的角度进行考量。
精确率和召回率
精确率,也被称作查准率,是指所有预测为正类的结果中,真正的正类的比例。
召回率,也被称作查全率,是指所有正类中,被分类器找出来的比例。
F1值:(readme文档).assets/gif.latex)]
对于上述两个公式的符号定义,是在二分类问题中,我们将关注的类别作为正类,其他类别作为负类别,因此,定义:
TP(True Positive):真正正类的数量,即分类为正类,实际也是正类的样本数量;FP(False Positive):假正类的数量,即分类为正类,但实际是负类的样本数量;FN(False Negative):假负类的数量,即分类为负类,但实际是正类的样本数量;TN(True Negative):真负类的数量,即分类是负类,实际也负类的样本数量。