利普希茨连续(Lipschitz continuous)及其应用
参考链接:
https://www.zhihu.com/question/51809602
https://zhuanlan.zhihu.com/p/27554191
https://blog.csdn.net/FrankieHello/article/details/105739610
目录
通俗解释
以陆地为例。
岛屿:不连续
一般陆地:连续
丘陵:李普希兹连续
悬崖:非李普希兹连续
山包:可导
平原:线性
半岛:非凸
想了半天用什么来表达亚连续(semi-continuity),好像只能用瀑布了
稍微具体点的话,李普希兹连续就是说,一块地不仅没有河流什么的玩意儿阻隔,而且这块地上没有特别陡的坡。其中最陡的地方有多陡呢?这就是所谓的李普希兹常数。
悬崖的出现导致最陡的地方有“无穷陡”,所以不是李普希兹连续。
定义
Lipschitz连续,要求函数图像的曲线上任意两点连线的斜率一致有界,就是任意的斜率都小于同一个常数,这个常数就是Lipschitz常数。
- 从局部看:我们可以取两个充分接近的点,如果这个时候斜率的极限存在的话,这个斜率的极限就是这个点的导数。也就是说函数可导,又是Lipschitz连续,那么导数有界。反过来,如果可导函数,导数有界,可以推出函数Lipschitz连续。
- 从整体看:Lipschitz连续要求函数在无限的区间上不能有超过线性的增长,所以这些
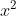 和
和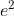 函数在无限区间上不是Lipschitz连续的。
函数在无限区间上不是Lipschitz连续的。
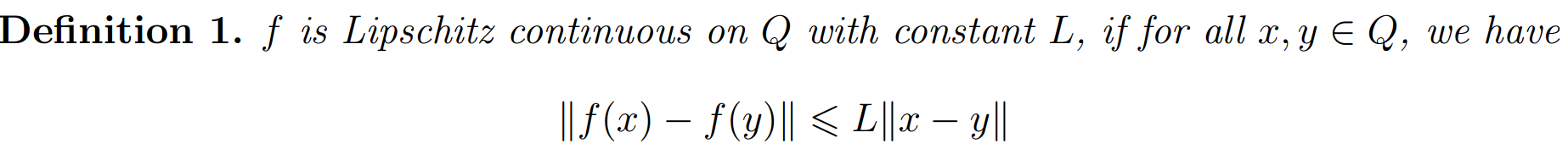
其中常数L 称为f 在区间Q 上的Lipschitz常数。
除了Lipschitz continuous之外,Lipschitz continuous gradient 和 Lipschitz continuous Hessian也是常用到的概念,它们都是由Lipschitz continuous概念延伸出来的。值得一提的是,很多论文中,尤其是关于凸优化的问题,Lipschitz continuous gradient的应用更为常见。

直观解释
Lipschitz continuous: 函数被一次函数上下夹逼
Lipschitz continuous gradient :函数被二次函数上下夹逼
Lipschitz continuous Hessian :函数被三次函数上下夹逼
在我看来,Lipschitz continuous 用在函数值上是为了不让函数值变化的太快;用在导函数上,是为了不让导函数变化的太快;用在Hessian上,是为了让Hessian不变化的太快。但他们都导致了一个很有意思的结果:这个Lipschitz continuous不管用在什么上,都使的函数被多项式上下夹逼,一方面便于我们处理,另一方面至少我们能控制一下函数的包络信息。


