2023-12-19 二叉搜索树的最小绝对差和二叉搜索树的众数和二叉树的最近公共祖先
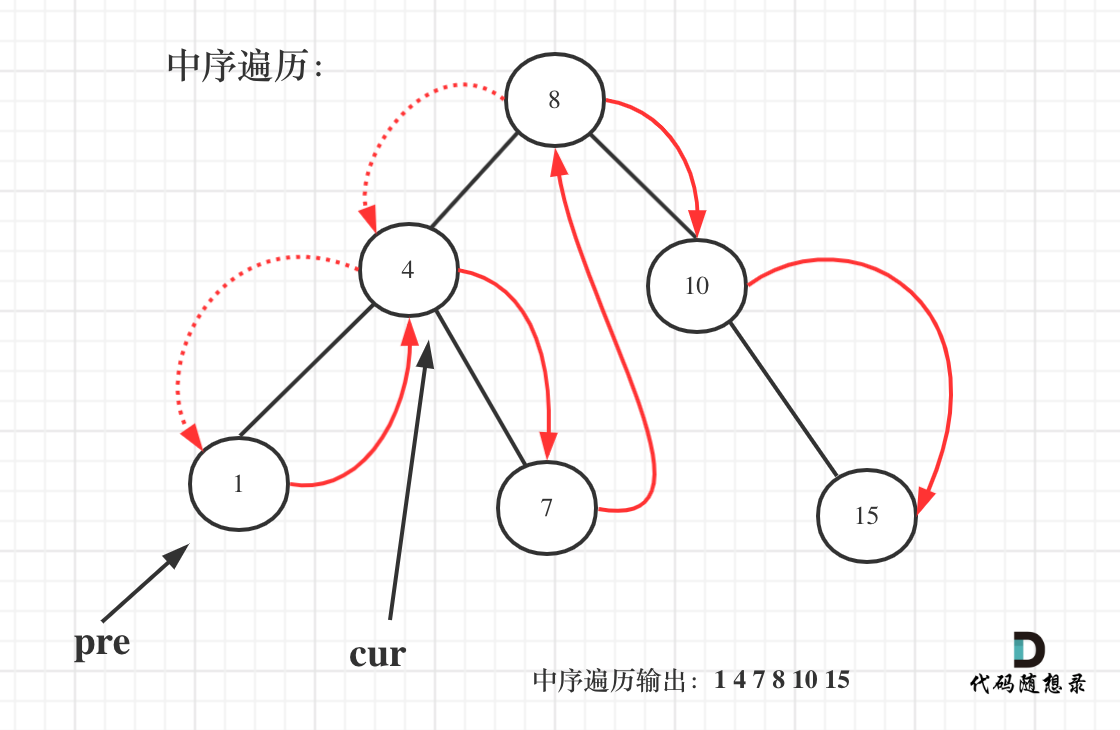
二叉搜索树的最小绝对差
关键信息:二叉搜索树表明了树有序的!遇到在二叉搜索树上求什么最值啊,差值之类的,就把它想成在一个有序数组上求最值,求差值
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
# 使用迭代法
if not root:
return
stack = []
result = []
while root or stack:
if root:
stack.append(root)
root = root.left
else:
node = stack.pop(-1)
result.append(node.val)
root = node.right
if len(result) < 2:
return
res = result[1] - result[0]
for i in range(2, len(result)):
res = min(res, result[i] - result[i - 1])
return res
# 使用递归来做
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
result = self.getMinimumDifference1(root)
min_res = result[1] - result[0]
for i in range(2,len(result)):
min_res = min(min_res, result[i] - result[i -1])
return min_res
def getMinimumDifference1(self, root: Optional[TreeNode]) -> int:
if not root:
return []
left = self.getMinimumDifference1(root.left) # 左
right = self.getMinimumDifference1(root.right) # 右
return left + [root.val] + right # 左加中加右
或者更加简洁一点的方法:
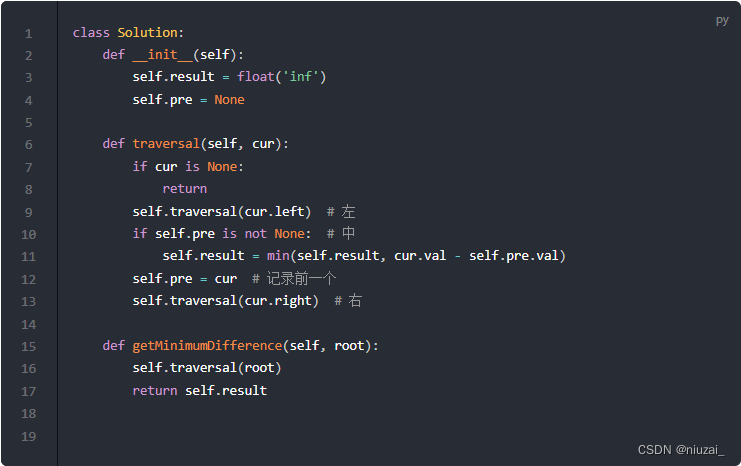
501. 二叉搜索树中的众数
思路:求众数首先先到的是HashMap!也就是字典!或者利用二叉搜索树是有序的特点存在字典中
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.dict_1 = {}
self.max = float('-inf')
def findMode(self, root: Optional[TreeNode]) -> List[int]:
self.findMode1(root)
print(self.dict_1,self.max)
result = []
for i,k in self.dict_1.items():
if k == self.max:
result.append(i)
return result
def findMode1(self, root: Optional[TreeNode]):
if not root:
return
if root.val in self.dict_1:
self.dict_1[root.val] += 1
else:
self.dict_1[root.val] = 1
if self.dict_1[root.val] >= self.max:
self.max = self.dict_1[root.val]
self.findMode1(root.left)
self.findMode1(root.right)
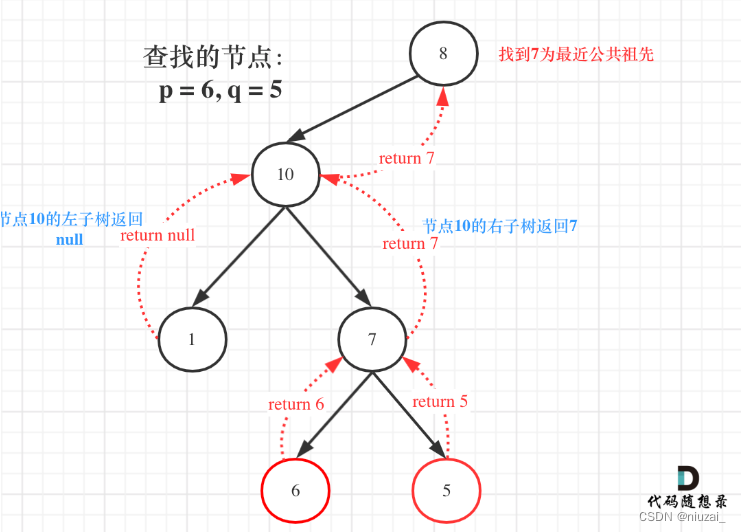
236. 二叉树的最近公共祖先
难点:出于惯性的思维,我们都是从上往下遍历的!而这道题需要我们从下往上遍历的,需要用到后续遍历!然后节点进行回溯一步一步往上传递!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
# 使用后续遍历的方法,可以从下往上进行处理!递归结束条件!!!
if root is None or root == p or root == q:
return root
left = self.lowestCommonAncestor(root.left, p , q) # 左
right = self.lowestCommonAncestor(root.right, p , q) # 右
# 中的处理逻辑!根据左右的结果判断!这个后续遍历就很重要了
if left and right:
return root
elif not left and right:
return right
elif left and not right:
return left
else:
return None #都没有出现p或q的情况的返回给上一层的内容!
或者精简版:
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root == q or root == p or root is None:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left is not None and right is not None:
return root
if left is None:
return right
return left
, p, q)
if left is not None and right is not None:
return root
if left is None:
return right
return left